PTA 树的同构（25 分）

Posted 2020-10-13

7-1 树的同构（25 分）

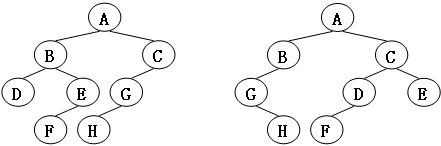
给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2，则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的，因为我们把其中一棵树的结点A、B、G的左右孩子互换后，就得到另外一棵树。而图2就不是同构的。

 

 

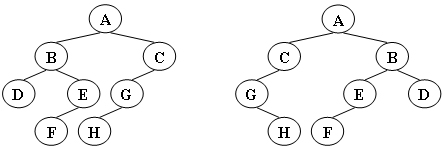
图1

图2

现给定两棵树，请你判断它们是否是同构的。

 

输入格式:

输入给出2棵二叉树树的信息。对于每棵树，首先在一行中给出一个非负整数N (≤10)，即该树的结点数（此时假设结点从0到N?1编号）；随后N行，第i行对应编号第i个结点，给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空，则在相应位置上给出“-”。给出的数据间用一个空格分隔。注意：题目保证每个结点中存储的字母是不同的。

输出格式:

如果两棵树是同构的，输出“Yes”，否则输出“No”。

输入样例1（对应图1）：

8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -

输出样例1:

Yes

输入样例2（对应图2）：

8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4

输出样例2:

No

emmmmmm   声明，下面的骚操作适合节点和边都比较少的，别怪我没提醒，多了就不对了，但是骚一字就够了

#include <bits/stdc++.h>// 根据度数判断
using namespace std;
const int maxn = 11;
int countsa[maxn];
int countsb[maxn];
int main()
{
    int n;
    scanf("%d",&n);
    char a,b,c;

    for(int i=0;i<n;i++)
    {
        int add = 2;
        cin>>a>>b>>c;
        if(b==‘-‘) add--;
        if(c==‘-‘) add--;
        countsa[a-‘A‘] +=add;
    }
    scanf("%d",&n);
    for(int i=0;i<n;i++)
    {
        int add = 2;
        cin>>a>>b>>c;
        if(b==‘-‘) add--;
        if(c==‘-‘) add--;
        countsb[a-‘A‘]+=add;
    }
    if(n==1) {cout<<"No"<<endl;
    return 0;}
    int i;
    for(i=0;i<n;i++)
    {
        if(countsa[i]!=countsb[i])
        {
            cout<<"No"<<endl;
            break;
        }
    }
    if(i==n)
        cout<<"Yes"<<endl;
}