信号与系统分析2022春季作业-参考答案:第十四次作业
Posted 卓晴
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了信号与系统分析2022春季作业-参考答案:第十四次作业相关的知识,希望对你有一定的参考价值。

作业要求链接: 信号与系统2022春季作业-第14次作业 : https://zhuoqing.blog.csdn.net/article/details/125103375
§14 参考答案
1.1 离散傅里叶变换
1.1.1 数据采样参数
◎ 求解:
(1) 数据采样时间间隔等于数据采样频率 f s f_s fs 的倒数。 根据要求信号频谱中最高频率 f M A X ≥ 5 k H z f_MAX \\ge 5\\,\\,kHz fMAX≥5kHz ,那么 f s ≥ 2 f M A X = 10 k H z f_s \\ge 2f_MAX = 10\\,\\,kHz fs≥2fMAX=10kHz ,因此数据采样时间间隔 T s = 1 f s = 1 2 ⋅ f M A X = 1 10 × 1 0 3 = 100 μ s T_s = 1 \\over f_s = 1 \\over 2 \\cdot f_MAX = 1 \\over 10 \\times 10^3 = 100\\mu s Ts=fs1=2⋅fMAX1=10×1031=100μs
(2) 根据频率间分辨率 f 1 ≤ 10 H z f_1 \\le 10Hz f1≤10Hz ,因此数据采样总时间 T 1 ≥ 1 f 1 = 1 10 = 100 m s T_1 \\ge 1 \\over f_1 = 1 \\over 10 = 100ms T1≥f11=101=100ms 那么采样数据点 N = T 1 T s = 0.1 100 × 1 0 − 6 = 1000 N = T_1 \\over T_s = 0.1 \\over 100 \\times 10^ - 6 = 1000 N=TsT1=100×10−60.1=1000 为了适应FFT算法,最终取 N = 1024 N = 1024 N=1024 。
1.1.2 频谱分析计算量
◎ 求解:
(1) 对于两个长度分别为 N , M N,M N,M 的序列,计算它们完全(线)卷积,所需要的实数乘法次数为 N ⋅ M N \\cdot M N⋅M ,实数加法次数为: ( N − 1 ) ( M − 1 ) \\left( N - 1 \\right)\\left( M - 1 \\right) (N−1)(M−1) 。
为了说明上述结论,可以由列表法求解序列卷积过程,展示了所有乘法和加法次数。具体可以参见下面两个说明。
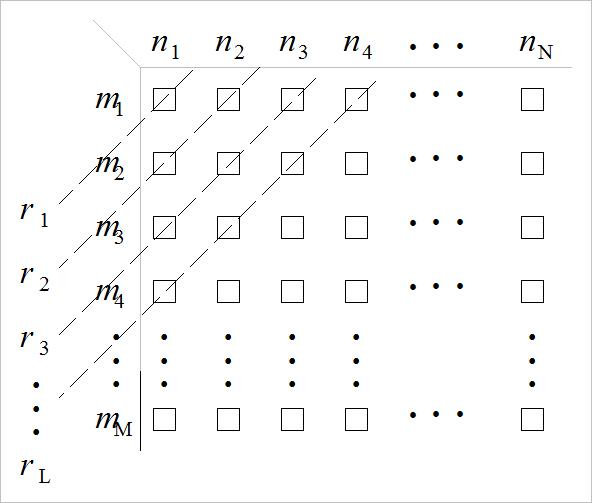
▲ 图1.1.1 表格法计算离散序列卷积示意图
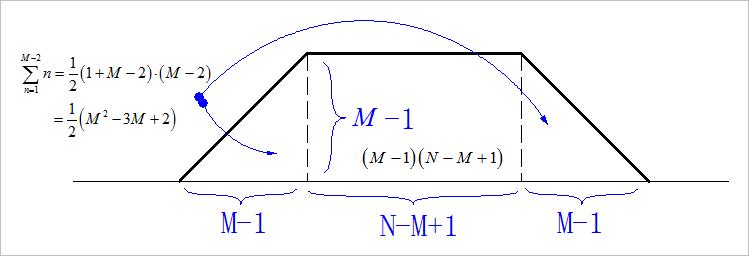
▲ 图1.1.2 以M<N为例,说明在卷积过程中加法次数
由此,可以知道在本题中,两个序列的长度分别为 240, 14。所以直接使用线卷积计算两个序列的卷积,实数乘法次数为 240 × 14 = 3360 240 \\times 14 = 3360 240×14=3360 ;实数加法次数为 ( 240 − 1 ) × ( 14 − 1 ) = 3107 \\left( 240 - 1 \\right) \\times \\left( 14 - 1 \\right) = 3107 (240−1)×(14−1)=3107 。
(2) 利用基-2的FFT, 完成 x [ n ] , h [ n ] x\\left[ n \\right],h\\left[ n \\right] x[n],h[n] 之间的线卷积,根据课件上给定的快速计算框架,其中需要:
- 将两个序列都通过补零达到超过 240+14-1=253,并且是 2 的整数次幂,因此将两个序列都补零到长度为 N = 256 N = 256 N=256 ;
计算过程需要的三次FFT的计算复杂度和一次变换域内的乘积。因此总的复数乘法次数为: N M = 3 × N 2 log 2 N + N = 3328 N_M = 3 \\times N \\over 2\\log _2 N + N = 3328 NM=3×2Nlog2N+N=2021年春季学期-信号与系统-第十四次作业参考答案-第三小题参考答案
2021年春季学期-信号与系统-第十四次作业参考答案-第一小题参考答案
2021年春季学期-信号与系统-第十四次作业参考答案-第五小题参考答案
2021年春季学期-信号与系统-第十四次作业参考答案-第八小题参考答案