2021年春季学期-信号与系统-第十三次作业参考答案
Posted 卓晴
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了2021年春季学期-信号与系统-第十三次作业参考答案相关的知识,希望对你有一定的参考价值。

▓ 第十三次作业各个小题参考答案:
- 2021年春季学期-信号与系统-第十三次作业参考答案-第一小题
- 2021年春季学期-信号与系统-第十三次作业参考答案-第二小题
- 2021年春季学期-信号与系统-第十三次作业参考答案-第三小题
- 2021年春季学期-信号与系统-第十三次作业参考答案-第四小题
- 2021年春季学期-信号与系统-第十三次作业参考答案-第五小题
- 2021年春季学期-信号与系统-第十三次作业参考答案-第六小题
- 2021年春季学期-信号与系统-第十三次作业参考答案-第七小题
- 2021年春季学期-信号与系统-第十三次作业参考答案-第八小题
- 2021年春季学期-信号与系统-第十三次作业参考答案-第九小题
- 2021年春季学期-信号与系统-第十三次作业参考答案-第十小题
- 2021年春季学期-信号与系统-第十三次作业参考答案-第十一小题
§01 第一小题
1. 如下图所示的反馈系统,回答以下各列问题:
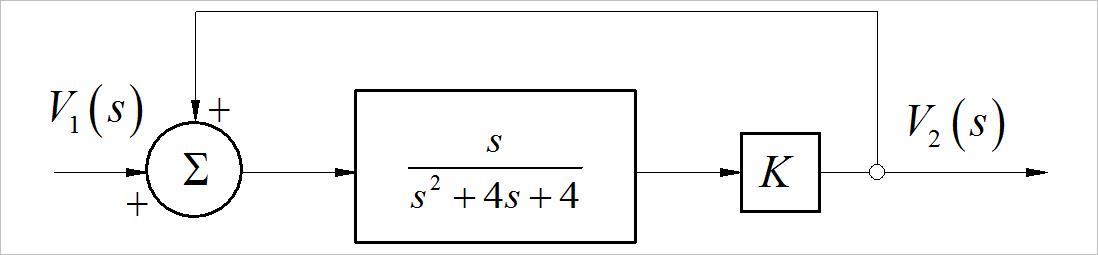
(1)写出: H ( s ) = V 2 ( s ) V 1 ( s ) H\\left( s \\right) = {{V_2 \\left( s \\right)} \\over {V_1 \\left( s \\right)}} H(s)=V1(s)V2(s)
(2)K满足什么条件时系统稳定?
(3)在临界稳定条件下,求系统的单位冲击响应 h ( t ) h\\left( t \\right) h(t)。
§02 第二小题
2.如下图所示的反馈系统,回答一下各问题:
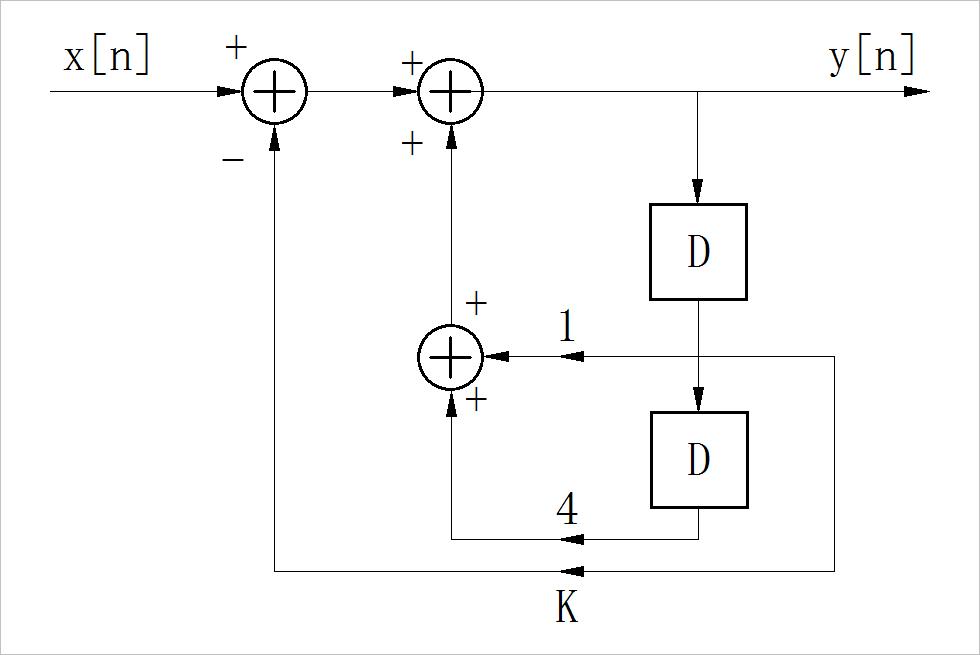
(1)写出:
H
(
z
)
=
Y
(
z
)
X
(
z
)
H\\left( z \\right) = {{Y\\left( z \\right)} \\over {X\\left( z \\right)}}
H(z)=X(z)Y(z);
(2)K 满足什么条件时系统稳定?
§03 第三小题
3. 离散时间系统如下图所示:
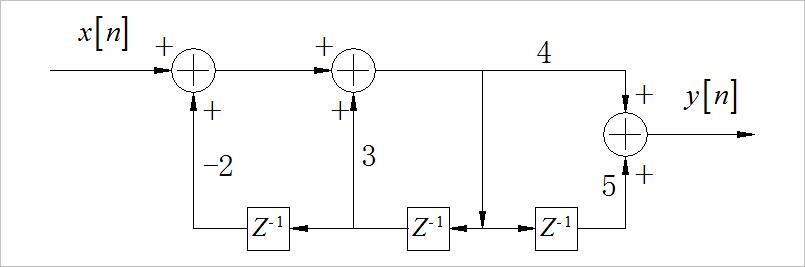
(1)求该系统的传递函数
H
(
z
)
H\\left( z \\right)
H(z);
(2)设系统的激励为:
x
[
n
]
=
[
(
−
1
)
n
+
(
−
2
)
n
]
u
[
n
]
x\\left[ n \\right] = \\left[ {\\left( { - 1} \\right)^n + \\left( { - 2} \\right)^n } \\right]u\\left[ n \\right]
x[n]=[(−1)n+(−2)n]u[n] 用z变换求该系统的零状态响应;
(3)已知:
x
[
n
]
=
δ
[
n
]
,
y
[
0
]
=
1
,
y
[
−
1
]
=
−
1
x\\left[ n \\right] = \\delta \\left[ n \\right],\\,\\,y\\left[ 0 \\right] = 1,\\,\\,y\\left[ { - 1} \\right] = - 1
x[n]=δ[n],y[0]=1,y[−1]=−1 用z变换求该系统的零输入相应;
提示:(2),(3)两步请参见第五章[5.7.2]中内容
§04 第四小题
4.已知离散时间因果系统的差分方程为:
(1) y [ n ] = 0.14 x [ n ] + 0.14 x [ n − 1 ] + 1.02 y [ n − 1 ] y\\left[ n \\right] = 0.14x\\left[ n \\right] + 0.14x\\left[ {n - 1} \\right] + 1.02y\\left[ {n - 1} \\right] y[n]=0.14x[n]+0.14x[n−1]+1.02y[n−1](2) y [ n ] = 0.5 x [ n ] − 0.3 x [ n − 2 ] − 2 y [ n − 1 ] − y [ n − 2 ] y\\left[ n \\right] = 0.5x\\left[ n \\right] - 0.3x\\left[ {n - 2} \\right] - 2y\\left[ {n - 1} \\right] - y\\left[ {n - 2} \\right] y[n]=0.5x[n]−0.3x[n−2]−2y[n−1]−y[n−2]
通过传递函数的极点位置判断该系统的稳定性。
§05 第五小题
5. 对于LTI系统,施加激励信号: x ( t ) = e − t u ( t ) x\\left( t \\right) = e^{ - t} u\\left( t \\right) x(t)=e−tu(t)系统的零状态输出为: y ( t ) = ( 1 2 e − t − e − 2 t + 2 e 3 t ) u ( t ) y\\left( t \\right) = \\left( {{1 \\over 2}e^{ - t} - e^{ - 2t} + 2e^{3t} } \\right)u\\left( t \\right) y(t)=(21e−t−e−2t+2e3t)u(t)求该系统的系统函数H(s),单位脉冲响应h(t)。
§06 第六小题
6.已知电路如下图所示,传递函数的零极点如下图所示,且H(0)=1;
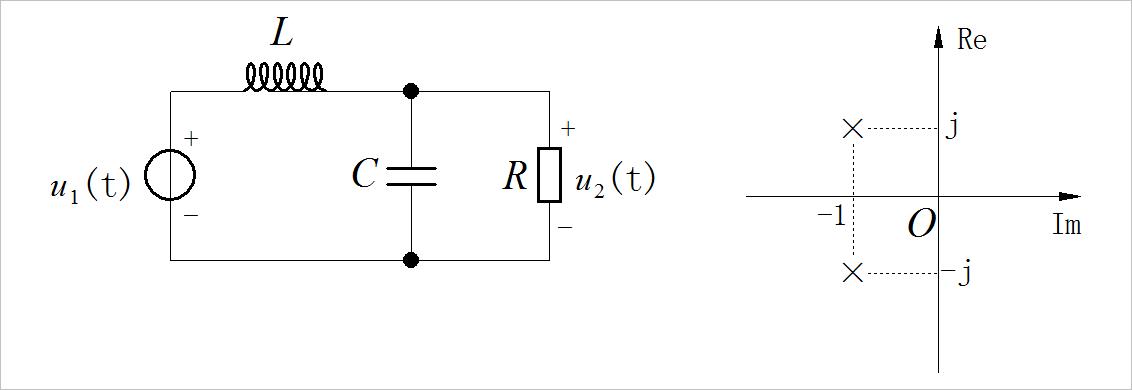
求 R,L,C的数值。
§07 第七小题
7. 下列Z变换中,那些是对应的因果系统的系统函数?
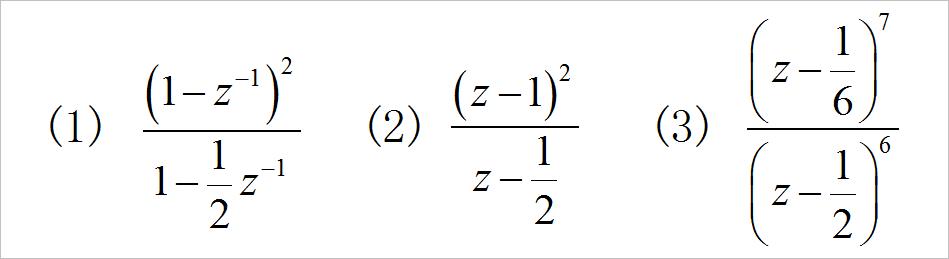
§08 第八小题
8.因果、稳定、LTI系统的传递函数H(s),该系统的输入为:
x
(
t
)
=
δ
(
t
)
+
e
s
0
t
+
x
1
(
t
)
x\\left( t \\right) = \\delta \\left( t \\right) + e^{s_0 t} + x_1 \\left( t \\right)
x(t)=δ(t)+es0t+x1(t)其中
x
1
(
t
)
x_1 \\left( t \\right)
x1(t)未知,
s
0
s_0
s0为复数常数。
由
x
(
t
)
x\\left( t \\right)
x(t)产生的输出信号为:
y
(
t
)
=
δ
(
t
)
−
6
e
−
t
u
(
t
)
−
1
2
e
4
t
cos
3
t
−
3
2
e
4
t
sin
3
t
y\\left( t \\right) = \\delta \\left( t \\right) - 6e^{ - t} u\\left( t \\right) - {1 \\over 2}e^{4t} \\cos 3t - {3 \\over 2}e^{4t} \\sin 3t
y(t)=δ(t)−6e−tu(t)−21e4tcos3t−23e4tsin3t求符合上述条件的传递函数。