三维坐标下判断P点是否在三角形ABC中
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了三维坐标下判断P点是否在三角形ABC中相关的知识,希望对你有一定的参考价值。
在网上找的都是二位坐标下的,我写个三维的吧
1.面积法
同二位坐标下一样,只需要判断三角形ABC的面积是否等于S_ABP+S_BCP+S_ACP。当然此方法需要开好几个根,不仅效率很低,还会损失精度,所以我使用的输入类型是int,并把误差控制到10E(-8)。里面还用到了一点向量的知识,但很好理解。代码如下:
1 #include<iostream> 2 #include<cmath> 3 #include<stdlib.h> 4 using namespace std; 5 class Point 6 { 7 private: 8 int x; 9 int y; 10 int z; 11 public: 12 void Setxyz(int x,int y, int z) 13 { 14 this->x = x; 15 this->y = y; 16 this->z = z; 17 } 18 int Getx(void) { return x; } 19 int Gety(void) { return y; } 20 int Getz(void) { return z; } 21 }; 22 class Vector3 23 { 24 private: 25 int x; 26 int y; 27 int z; 28 public: 29 void Setx(int x) { this->x = x; } 30 void Sety(int y) { this->y = y; } 31 void Setz(int z) { this->z = z; } 32 int Getx(void) { return x; } 33 int Gety(void) { return y; } 34 int Getz(void) { return z; } 35 }; 36 Vector3 toVector3(Point M, Point N) 37 { 38 Vector3 MN; 39 MN.Setx(N.Getx() - M.Getx()); 40 MN.Sety(N.Gety() - M.Gety()); 41 MN.Setz(N.Getz() - M.Getz()); 42 return MN; 43 } 44 bool isTri(Point A, Point B, Point C) 45 { 46 Vector3 AB = toVector3(A, B); 47 Vector3 BC = toVector3(B, C); 48 if ((BC.Getx()*AB.Gety() == AB.Getx()*BC.Gety()) && 49 (BC.Getx()*AB.Getz() == AB.Getx()*BC.Getz())) 50 return 0; 51 else 52 return 1; 53 } 54 double Distance(Point M, Point N) 55 { 56 Vector3 MN; 57 MN = toVector3(M, N); 58 double Dis_MN = sqrt((double)(MN.Getx()*MN.Getx ()+ MN.Gety()*MN.Gety() + MN.Getz()*MN.Getz())); 59 return Dis_MN; 60 } 61 double S(Point A,Point B,Point C) 62 { 63 double c = Distance(A,B); 64 double b= Distance(A, C); 65 double a= Distance(B, C); 66 double p = (a+b+c)/2; 67 double s = sqrt(p*(p - a)*(p - b)*(p - c));//海伦公式 68 return s; 69 } 70 bool PointInTri(Point A, Point B, Point C, Point P) 71 { 72 double S1 = S(A, B, C); 73 double S2 = S(A, B, P); 74 double S3 = S(B, C, P); 75 double S4 = S(A, C, P); 76 if (abs(S1 -(S2 + S3 + S4))<=pow(10,-8))//因为有精度损失 77 return 1; 78 else 79 return 0; 80 } 81 82 int main(void) 83 { 84 Point A, B, C, P; 85 int Ax, Ay, Az; 86 int Bx, By, Bz; 87 int Cx, Cy, Cz; 88 int Px, Py, Pz; 89 cout << "请输入ABC三个点成三角形(必须是整数型)\\n" << endl; 90 while (1) 91 { 92 cout << "A点坐标:" << endl; 93 cin >> Ax >> Ay >> Az; 94 A.Setxyz(Ax, Ay, Az); 95 cout << "B点坐标:" << endl; 96 cin >> Bx >> By >> Bz; 97 B.Setxyz(Bx, By, Bz); 98 cout << "C点坐标:" << endl; 99 cin >> Cx >> Cy >> Cz; 100 C.Setxyz(Cx, Cy, Cz); 101 if (isTri(A, B, C)) 102 { 103 cout << "P点坐标:" << endl; 104 cin >> Px >> Py >> Pz; 105 P.Setxyz(Px, Py, Pz); 106 if (PointInTri(A, B, C, P)) 107 cout << "点P在三角形ABC内" << endl; 108 else 109 cout << "点P在三角形ABC外" << endl; 110 } 111 else 112 cout << "ABC三点一线,组不成三角形" << endl; 113 cout << "输入q退出,输入c继续" << endl; 114 char Sign; 115 cin >> Sign; 116 if (Sign == ‘q‘)break; 117 } 118 system("pause"); 119 return 0; 120 }
2.向量法
先考虑ABCP四点共面,如下图:(我是知识的搬运工。。。)
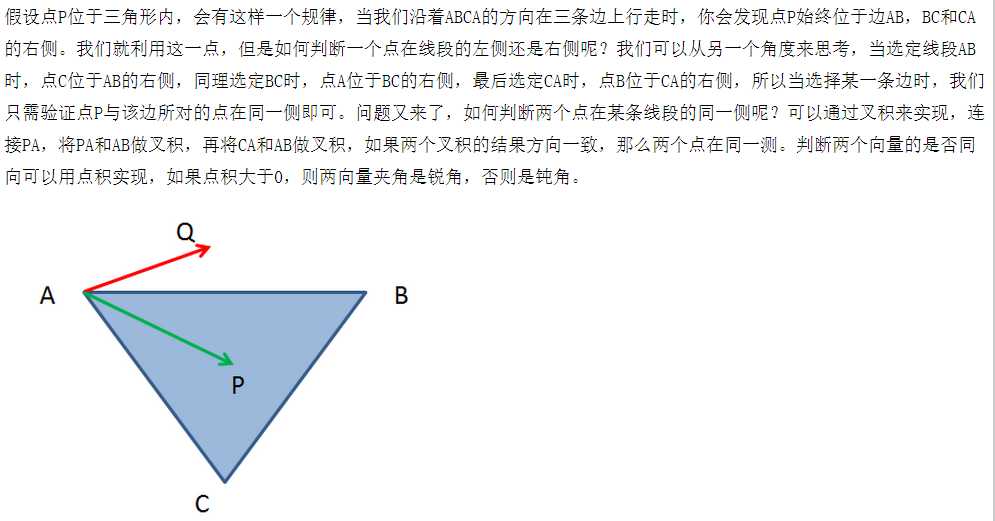
然后我们再考虑如何判断四点共面:求出AB与AC的叉积,再判断AP与叉积是否垂直,即点积是否为0
#include<iostream> #include<stdlib.h> using namespace std; class Point { private: double x; double y; double z; public: void Setxyz(double x,double y,double z) { this->x = x; this->y = y; this->z = z; } double Getx(void) { return x; } double Gety(void) { return y; } double Getz(void) { return z; } }; class Vector3 { private: double x; double y; double z; public: void Setx(double x) { this->x = x; } void Sety(double y) { this->y = y; } void Setz(double z) { this->z = z; } double Getx(void) { return x; } double Gety(void) { return y; } double Getz(void) { return z; } Vector3 Cross(Vector3 b)//向量积,即叉乘 { Vector3 aCrob; aCrob.x = this->y*b.z - b.y*this->z; aCrob.y = this->z*b.x - b.z*this->x; aCrob.z = this->x*b.y - b.x*this->y; return aCrob; } double Dot(Vector3 a)//向量点乘 { return this->x*a.x + this->y*a.y + this->z*a.z; } }; Vector3 toVector3(Point M, Point N) { Vector3 MN; MN.Setx(N.Getx() - M.Getx()); MN.Sety(N.Gety() - M.Gety()); MN.Setz(N.Getz() - M.Getz()); return MN; } bool Side(Point A,Point B, Point C, Point P)//是否在同一侧 { Vector3 AB = toVector3(A,B); Vector3 AC = toVector3(A,C); Vector3 AP = toVector3(A,P); Vector3 a1 = AB.Cross(AC); Vector3 a2 = AB.Cross(AP); return a1.Dot(a2)>=0; } bool PointInTri(Point A, Point B, Point C, Point P) { return Side(A, B, C, P) && Side(B, C, A, P) && Side(C, A, B, P); } bool isSnameDirction(Vector3 AB, Vector3 BC) { if ((BC.Getx()*AB.Gety() == AB.Getx()*BC.Gety()) && (BC.Getx()*AB.Getz() == AB.Getx()*BC.Getz())) return 1; else return 0; } bool isSnamePlane(Point A, Point B, Point C, Point P) { Vector3 AB = toVector3(A, B); Vector3 AC = toVector3(A, C); Vector3 AP = toVector3(A, P); Vector3 n1 = AB.Cross(AC); int flag; flag = AP.Dot(n1);//两向量垂直时为0 if (flag==0) return 1; else return 0; } bool isTri(Point A, Point B, Point C) { Vector3 AB = toVector3(A, B); Vector3 BC = toVector3(B, C); if (isSnameDirction(AB, BC)) return 0; else return 1; } int main(void) { /* 绝对值小的double类型值不断相乘会发生精度遗失 比如A(0,0,0) B(0,1,0) C(1,0,0) P(0.1,0.1,0.01) 建议输入整型 */ Point A, B, C, P; double Ax, Ay, Az; double Bx, By, Bz; double Cx, Cy, Cz; double Px, Py, Pz; cout<< "请输入ABC三个点成三角形\\n" << endl; while (1) { cout << "A点坐标:" << endl; cin >> Ax >> Ay >> Az; A.Setxyz(Ax, Ay, Az); cout << "B点坐标:" << endl; cin >> Bx >> By >> Bz; B.Setxyz(Bx, By, Bz); cout << "C点坐标:" << endl; cin >> Cx >> Cy >> Cz; C.Setxyz(Cx, Cy, Cz); if (isTri(A, B, C)) { cout << "P点坐标:" << endl; cin >> Px >> Py >> Pz; P.Setxyz(Px, Py, Pz); if (isSnamePlane(A, B, C, P)) { if (PointInTri(A, B, C, P)) cout << "点P在三角形ABC内" << endl; else cout << "点P在三角形ABC外" << endl; } else cout << "点P都ABC所确定的平面,更不可能在三角形ABC内" << endl; } else cout << "ABC三点一线,组不成三角形" << endl; cout << "输入q退出,输入c继续" << endl; char Sign; cin >>Sign; if (Sign == ‘q‘)break; } system("pause"); return 0; }
2.1向量法plus
上个方法直接从二维推到了三维,其实我们被忽悠了,判断向量是否同向我们不是一直用λ的吗?上一个代码中的isSnameDirction函数就是从此转换过来的。(他忽悠我们的目的是在二维中减少运算)再考虑当四点不共面时,可知原来的两个叉积所成的夹角为(0,,180),又考虑四点在同一平面内P却在三角形外,两叉积夹角为180。所以我们只需要判断三次两叉积同向即可,更改Side函数内代码,并删除isSnamePlane函数,Side函数代码如下
bool Side(Point A, Point B, Point C, Point P)//是否在同一侧
{
Vector3 AB = toVector3(A, B);
Vector3 AC = toVector3(A, C);
Vector3 AP = toVector3(A, P);
Vector3 a1 = AB.Cross(AC);
Vector3 a2 = AB.Cross(AP);
if (isSnameDirction(a1,a2))
return 1;
else
return 0;
}
2.2向量法++(最下面的链接说此法为重心法,我实在想不出它和重心有啥关系,还有我又按照评论给的建议精简此方法,于是我叫它究极向量法)
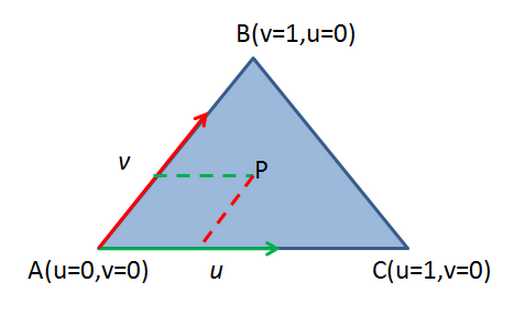
若四点共面,可知AP=u * AC + v * AB(以两点表示的都是向量)
如果系数u或v为负值,那么相当于朝相反的方向移动,即BA或CA方向。那么如果想让P位于三角形ABC内部,u和v必须满足什么条件呢?有如下三个条件
u >= 0 v >= 0 u + v <= 1
证明如下图;当P在BC边上(帮你理解,证明不规范)
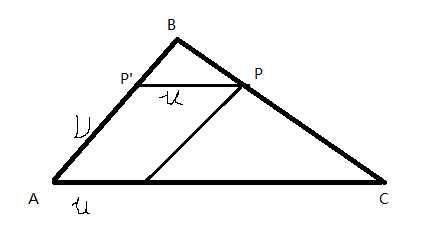
由三角形BPP‘与三角形ABC相似得P‘P=u*AC,得P‘B=u*AB,即u*AB+v*AB=AB,得u+v=1,只要u和v一个在变小都会使P在三角形内,反之即会在外,于是得u+v<=1
令v0 = AC, v1 = AB, v2 = AP,则v2 = u * v0 + v * v1,现在是一个方程,两个未知数,无法解出u和v,将等式两边分别点乘v0和v1的到两个等式
(v2) ? v0 = (u * v0 + v * v1) ? v0
(v2) ? v1 = (u * v0 + v * v1) ? v1
注意到这里u和v是数,而v0,v1和v2是向量,所以可以将点积展开得到下面的式子。
v2 ? v0 = u * (v0 ? v0) + v * (v1 ? v0) // 式1
v2 ? v1 = u * (v0 ? v1) + v * (v1? v1) // 式2
解这个方程得到
u = ((v1?v1)(v2?v0)-(v1?v0)(v2?v1)) / ((v0?v0)(v1?v1) - (v0?v1)(v1?v0))
v = ((v0?v0)(v2?v1)-(v0?v1)(v2?v0)) / ((v0?v0)(v1?v1) - (v0?v1)(v1?v0))
由柯西不等式:对任意向量v0, v1: v0^2 * V1^2 >= (v0 ? v1)^2。又v0, v1不共线,所以等号不成立,即公共分母>0
设 a = v0 ? v0, b = v1 ? v1, c = v0 ? v1,d = v2 ? v0, e = v2 ? v1, 公共分母 f = a * b - c* c,令x = b * d - c * e; y = a * e - c * d
则:u = x / f, v = y / f 由: u >= 0, v >= 0, u + v <= 1, 和f > 0 有:x >= 0, y >= 0, x + y - f <= 0
重写PointInTri函数代码
bool PointInTri(Point A, Point B, Point C, Point P)
{
Vector3 v0 = toVector3(A, C);
Vector3 v1 = toVector3(A, B);
Vector3 v2 = toVector3(A, P);
double a = v0.Dot(v0);
double b = v1.Dot(v1);
double c = v0.Dot(v1);
double d = v2.Dot(v0);
double e = v2.Dot(v1);
double f = a * b - c * c;
double x = b * d - c * e;
double y = a * e - c * d;
if ((x >= 0) && (y >= 0) && (x + y - f <= 0))
return 1;
else
return 0;
}
需要注意:我们开始推理时默认四点共面,若四点不共面,最开始的等式AP=u * AC + v * AB,便不可能存在。所以我们要保留2.1的isSnamePlane函数。
3.射线和三角形的相交检测
射线和三角形的相交检测具体过程就查看链接http://www.cnblogs.com/graphics/archive/2010/08/09/1795348.html
大致思路先确定射线OP是否与三角形ABC相交,若相交再判断交点是否为P。我猜这个才是实际中用到的吧(还有个内角和法,效率跟第一种方法差不多,不讲了,有兴趣的参考文献里有)。
总结:哎,英语没学好Same啊,多加了个n。。。
参考文献:
http://www.cnblogs.com/graphics/archive/2010/08/05/1793393.html
以上是关于三维坐标下判断P点是否在三角形ABC中的主要内容,如果未能解决你的问题,请参考以下文章
给定三角形ABC和一点P(x,y,z),判断点P是否在ABC内