2D空间中判断一点是否在三角形内

Posted 2020-08-21 HONT blog

要注意如果是XY坐标轴的2D空间，要取差乘分量z而不是y。

 

实现原理是，将三角形ABC三个边(AB,BC,CA)分别与比较点判断差乘，如果这3个差乘结果表示的方向一致，说明就在三角形内。

 

效果：

 

 

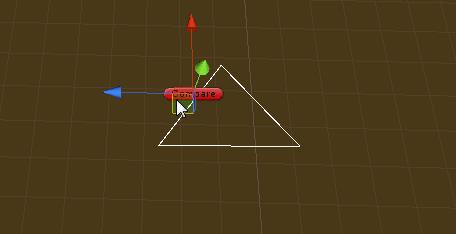
代码(Unity3D)：

using UnityEngine;
using System.Collections;
using System.Collections.Generic;

public class TriangleCollider : MonoBehaviour
{
    public const float ERROR = 0.05f;
    public Transform trianglePoint1;
    public Transform trianglePoint2;
    public Transform trianglePoint3;
    public Transform comparePoint;


    public bool IsContract(Vector3 comparePoint)
    {
        var dir1 = trianglePoint2.position - trianglePoint1.position;
        var dir2 = trianglePoint3.position - trianglePoint2.position;
        var dir3 = trianglePoint1.position - trianglePoint3.position;

        var cross1 = Mathf.Sign(Vector3.Cross(dir1, comparePoint - trianglePoint1.position).y);
        var cross2 = Mathf.Sign(Vector3.Cross(dir2, comparePoint - trianglePoint2.position).y);
        var cross3 = Mathf.Sign(Vector3.Cross(dir3, comparePoint - trianglePoint3.position).y);

        var dir = Mathf.Approximately(cross1, cross2) ? cross3 : Mathf.Approximately(cross1, cross3) ? cross2 : cross1;

        cross1 = Mathf.Sign(Vector3.Cross(dir1, comparePoint - trianglePoint1.position).y + -dir * ERROR);
        cross2 = Mathf.Sign(Vector3.Cross(dir2, comparePoint - trianglePoint2.position).y + -dir * ERROR);
        cross3 = Mathf.Sign(Vector3.Cross(dir3, comparePoint - trianglePoint3.position).y + -dir * ERROR);

        return Mathf.Approximately(cross1, cross2) && Mathf.Approximately(cross2, cross3);
    }

    void OnDrawGizmos()
    {
        if (comparePoint == null) return;

        var oldColor = Gizmos.color;

        if (IsContract(comparePoint.position))
            Gizmos.color = Color.red;

        Gizmos.DrawLine(trianglePoint1.position, trianglePoint2.position);
        Gizmos.DrawLine(trianglePoint2.position, trianglePoint3.position);
        Gizmos.DrawLine(trianglePoint3.position, trianglePoint1.position);

        Gizmos.color = oldColor;
    }
}

 

为了加误差，所以多做了3次差乘。不过使用起来还算可以