stata的时间序列分析中如何实现对数据的一阶差分，最好指令写出来·谢谢。。。。。

Posted 2023-04-24

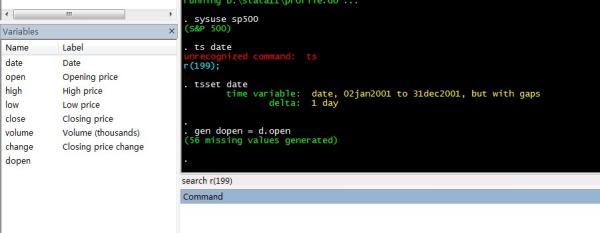
如果是连贯的时间序列

tsset date

gen d_price = d.price   // 一阶差分

如果不连贯

gen date_c = _n

tsset date_c

gen d_price = d.price 

参考技术A gen id=_n
tsset id
gen x=d.y

时间序列分析

参考技术A

在R中生成时间序列的前提是我们将分析对象转成时间序列函数对象，包括观测值、起始时间、种植时间、及周期（月、季度、年）的结构。这些都能通过ts( )函数实现。

R语言中，对时间序列数据进行分析处理时，使用差分函数要注意：差分函数diff()不带参数名的参数指滞后阶数，也就是与滞后第几阶的数据进行差分。如果要指定差分的阶数，则一定要使用带名称的参数:diff=2。

例如： sample表示样本数据。

1、diff(sample,2)表示是对滞后2阶的数据进行差分，一阶差分，等同于： diff(sample,lag=2)

2、diff(sample,diff=2)才是表示二阶差分

意：在函数中尽量避免使用没有命名的参数。在《时间序列分析及应用-R语言（第2版）》中，P315，描述到： 我们得到的教训就是，除非完全了解相关参数的位置，否则使用未命名参数是非常危险的。

截尾是指时间序列的自相关函数（ACF）或偏自相关函数（PACF）在某阶后均为0的性质（比如AR的PACF）；

拖尾是ACF或PACF并不在某阶后均为0的性质（比如AR的ACF）。

拖尾 ：始终有非零取值，不会在k大于某个常数后就恒等于零(或在0附近随机波动)

截尾 ：在大于某个常数k后快速趋于0为k阶截尾

AR模型：自相关系数拖尾，偏自相关系数截尾；

MA模型：自相关系数截尾，偏自相关函数拖尾；

ARMA模型：自相关函数和偏自相关函数均拖尾。

根据输出结果， 自相关函数图拖尾，偏自相关函数图截尾 ，且n从2或3开始控制在置信区间之内，因而可判定为AR(2)模型或者AR(3)模型。