时间序列分析第一章 差分方程

Posted 2021-05-02 痕风雨

        时间序列分析关注事件或者说变量在时间上的动态变化情况。如果将时间人为分期，并记变量y在第t期的值为y_t，那么将变量在第t期的值y_t与另外的变量w_t及第t期以前的值（如y_t-1）联系起来的方程即为差分方程。下面首先介绍一阶差分方程，然后介绍p阶差分方程。

一、一阶差分方程

• 一阶差分方程的概念
  

        一阶差分方程为：

y_t = Φy_t-1+w_t

这个动态方程将变量在第t期的值y_t与变量w_t及变量在第t-1期的值联系起来。在后面的分析中，w_t将被处理为随机变量，但在目前，我们先将其看作一期期的确定值。

• 用递归法求解差分方程

        假定已知条件为：y_-1和w_t,其中t=0,1,2,...

        在每个时期，我们都有一个方程将当期的y与前一期的y与当期的w联系起来，从而在已知y_-1和w_t在任意时期的值时，我们可以通过递归模拟出这个动态过程，进而求出y在每一时期的值。

第0期   y₀= Φy_-1+w₀

第1期   y₁= Φy₀+w₁

第2期   y₂= Φy₁+w₂

•              •

•              •

•              •

第t期    y_t= Φy_t-1+w_t

_{进而，y1= Φy0+w1}=Φ(Φy_-1+w₀)=Φ²y_-1+Φw₀+w₁

_{y2= Φy1+w2}=Φ(Φ²y_-1+Φw₀+w₁)=Φ³y_-1+Φ²w₀+Φw₁+w₂

_{依此类推，可得}

• _动态乘子

        _{通过递归法模拟一阶差分方程，我们将yt表示为y-1与w的历史值的线性函数，这让我们很容易地看到w的各期值对yt的影响，如w0对yt的影响为：}

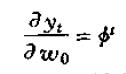
我们可以将y_t+j表示为y_{t-1和w的历史值的线性函数（这里先贴图，后面有时间再打公式）：}

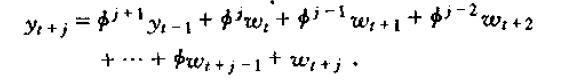
_从而，wt_对yt+j_{的影响为：}

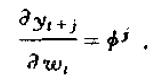
这里就能很明显地看出，动态乘子（我理解为w的某一期值对y的某一期值的影响系数）只取决于时间间隔 j，而与时间t无关。

        从动态乘子的表达式也可以看出y对w的动态响应与Φ的值密切相关。当0<Φ<1,随着时间间隔 j 的增大，w的影响以几何级数的速度趋于0；当-1<Φ<0，w对y的影响会震荡收敛于0；当Φ>1或Φ<-1时，动态乘子将以指数速度增加（不知道是不是所谓的爆炸过程），只不过都Φ为负时是一个振荡发散过程。因此，当|Φ|<1，差分方程是稳定(收敛)的，当|Φ|>1时系统是发散的。而对于边界情况Φ=1,式子变为

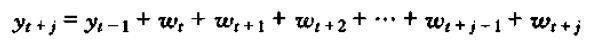
即w的每一历史值对y的影响均为1,w每增加一单位将导致y永久性地增加一单位：

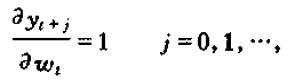
接下来我们考虑w对y的所有现值的影响效应，假设利率为r，则t时刻的现值为

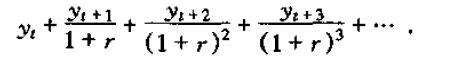
记β=1/(1+r)为折现因子，则现值为

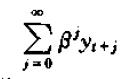
将该式对wt求偏导有：

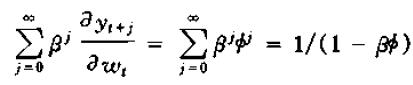
        对于动态乘子的计算，该式只关心w_t增加一单位同时w_t+1及以后的未来值均不改变时对y的影响，即它计算的是w的某一时期的单个冲击对y的某一时期的影响效应，所以也称动态乘子式为脉冲响应函数。有时我们可能更关心w的永久变化对y的影响效应，永久变化的意思是说从某一期开始，w的值永久性增加1个单位，对y的影响为：

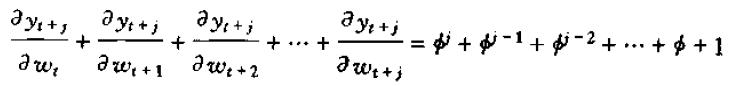
当|Φ|<1且j趋于无穷时，我们就得到了w对y的长期效应：

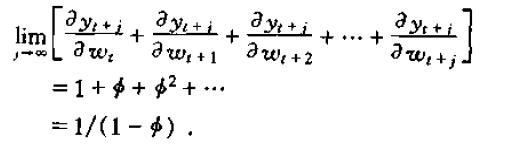
另一个相关的问题是考虑w某一时期的一个冲击对y各个时期的累积影响效应为：

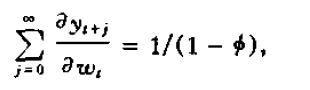
注意w的冲击对y的累积效应等于w的永久变化对y的某一时期的长期效应。

二、p阶差分方程

• p阶差分方程的概念

  
  

  

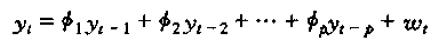
该动态方程将第t期的值与p阶滞后性及wt关联起来，称之为p阶差分方程。

        首先定义(px1)的向量ξt为：

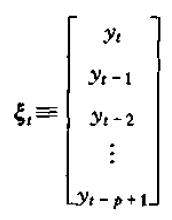
定义(pxp)的矩阵F为：

定义(px1)的向量vt为：

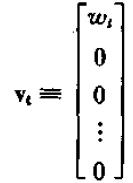
则有以下一阶向量差分方程：

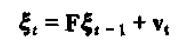
简单验证可知该方程的第一个分量表达式即为前面的p阶差分方程。将p阶差分方程转化为一阶向量差分方程可以类比一阶差分方程的思路去解p阶差分方程。

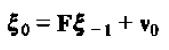
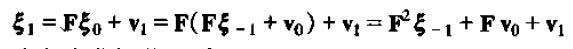
按照上式递归：

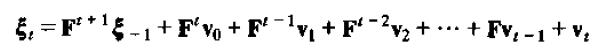
将这个结果转化为ξ和v的定义式，有：

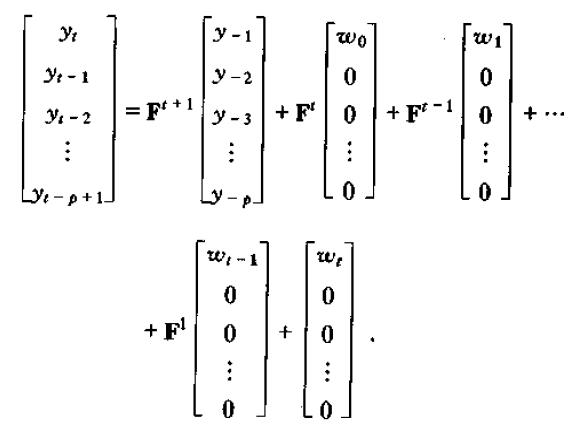
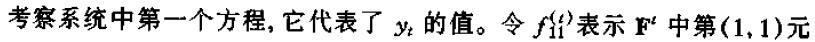
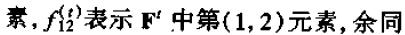。则该系统的第一个方程可以写为：

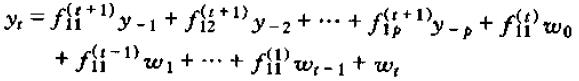
将式子推广：

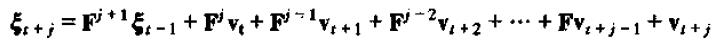
同样的方法可以得出：

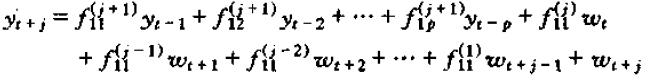
从而，p阶差分方程的动态乘子式为：

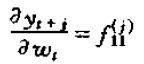
对于该动态乘子的具体数值，我们可以通过数值模拟得出。步骤如下

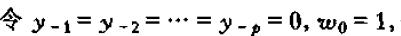并且令其他的所有w为0，然后递归到第t期得到的y值即为yt对w0的脉冲响应。

        尽管我们可以通过数值模拟的到任意一个我们关心的脉冲响应，但对动态乘子进行简单分析还是很有必要的。由前面已经，动态乘子等于F的j次方的第(1,1)个元素给出，矩阵论告诉我们该元素可以有F矩阵的特征值容易地给出。解方程：

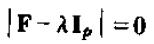
即可得到F的所有特征值。对于p阶差分方程，该方程实质上是关于λ的p阶方程，将其展开并处理即可得到如下形式

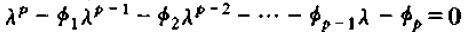
下面分两种情形继续讨论：

（1）F非奇异，F有p个不同的特征值

（2）F不是可逆矩阵，F存在相同的特征值

• F有p个不同的特征值

        由矩阵论我们知道，当(pxp)的矩阵F有P个不同的特征值时，则存在一个非奇异矩阵T，使得

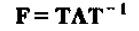
其中，Λ是一个主对角线元素为F的特征值，其余元素为0的(pxp)对角矩阵，即：

从而

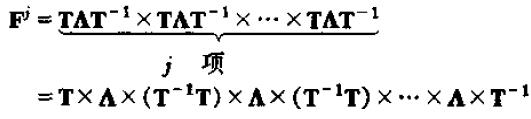
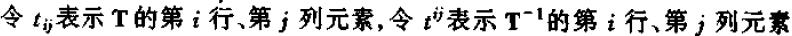
则可以展开为：

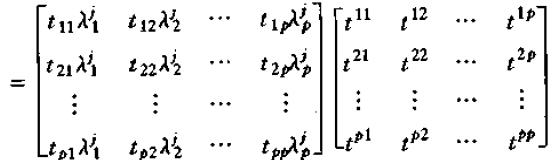
从而动态乘子式可以表示为：

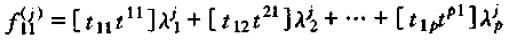
或

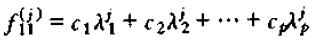
其中：

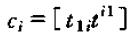
从而Ci的和为

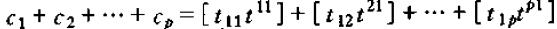 = 1

因为该和式即为T•T-1的第(1,1)个元素。综上,p阶差分方程的动态乘子式的用F特征值表示的形式为：

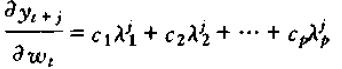
其中，

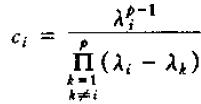
接下来我们对P=2的特殊情形进行详细讨论。

• 二阶差分系统

        二阶差分方程的特征方程为：

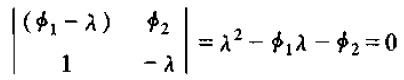
可以解出两个特征值为：

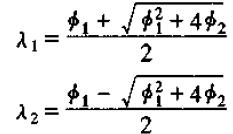
当Φ1²+4Φ2>0时，两个特征值均为实数。当λ1>1时，即λ

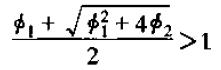
或者

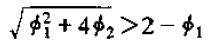
首先，当Φ1>=2时，上式明显成立，当Φ1<2时，两边平方得

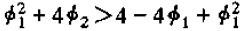
或

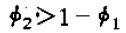
时，λ1>1。

同理，当λ2<-1时,

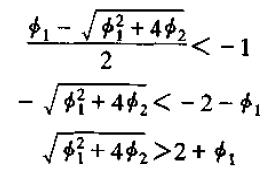
当Φ1<-2时，上式恒成立，当Φ1>-2时，两边平方得

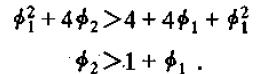
时，λ2<-1。见下图

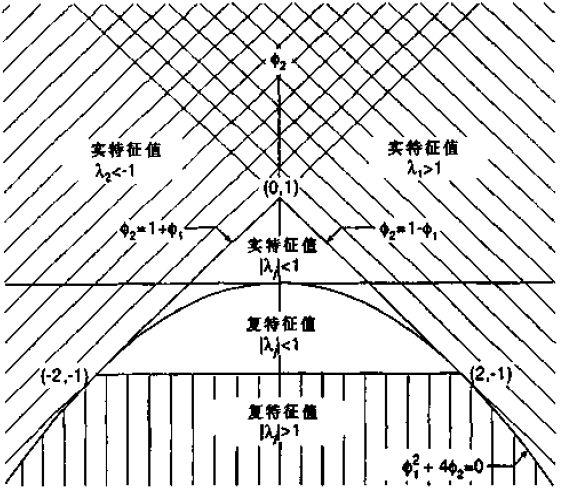
当Φ1与Φ2组成的坐标点落在直线Φ2=1+Φ1的左上方或者落在直线Φ2=1-Φ1的右上方时，系统均不稳定，即λ1或λ2其中之一的绝对值大于1，二阶差分方程就不稳定。

        当Φ1²+4Φ2<0时，两个特征值均为复数且共轭，可以写成以下形式

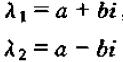
a，b可以用Φ1与Φ2表示为：

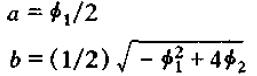
为方便进行计算，我们可以将复数转换为极坐标形式

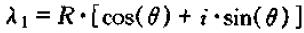
其中

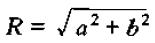
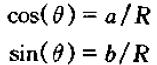
进而可以写为指数形式：

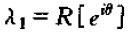
因此，

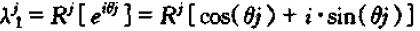
同理可得（λ1与λ2共轭），

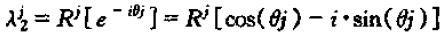
所以，

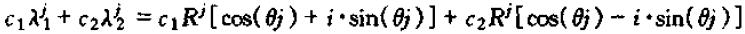
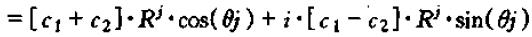
上式看着似乎还是一个复数，不过，实际上，上式是实数。因为λ1与λ2为共轭复数的情形下，c1与c2也为共轭复数，他们可以写为：

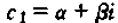
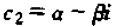
带入上式，可得：

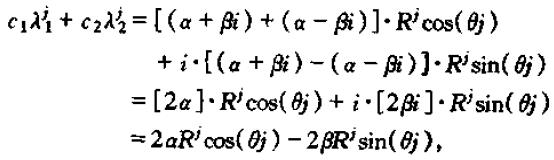
可以看到，当R<1时，动态乘子随 j 的增大会振荡收敛于0；当R=1时，动态乘子是关于 j 的周期函数，周期由2π/θ给出；当R>1时，动态乘子是一个振荡发散过程。如图

当Φ1²+4Φ2<0时，即（Φ1，Φ2）位于图中抛物线以下时，λ1，λ2为共轭复数。又由

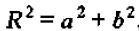
可得

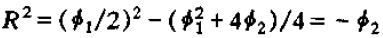
当Φ2<-2时，|R|>1，二阶差分系统振荡发散。即图中位于Φ2=-2以下的点全都不稳定。

        综上所述，只有当（Φ1，Φ2）落在图中三角形区域内时，二阶差分系统才是稳定的。

• F具有重复的特征值

        这种情况的相关式子的推导计算更为复杂，但思路大体一致。假设F有重复的特征值并且具有s<p个线性独立的特征向量，利用Jordan分解有：

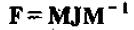
其中，M为(pxp)矩阵，J 的形式为

其中,

所以，

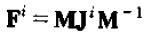
其中，

可以看到，只要知道 J 的具体值，就能够向前面一样讨论出动态乘子的表达式。

• 长期与现值的计算

        到目前为止，我们一直在讨论动态乘子即脉冲响应的情况，接下来让我们一起看看P阶差分系统的长期效应与w对现值的影响。

        若F的所有特征值的模小于1，则当 j 很大时，F^j 趋于0，从而我们可以将yt看着w的无限期历史值的解：

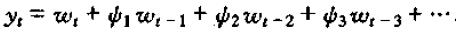
其中ψj即脉冲响应由 F^j 第(1,1)个元素给出。

        计算w的暂时冲击对y的现值的影响同样重要，首先有

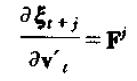
v的变化对ξ的现值影响为

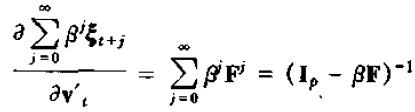
进而，w对y的现值影响为

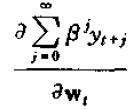
这实际上就是上述矩阵的第(1,1)个元素，并且其值为

上式中，令β=1即可得到w的短暂冲击对y的长期效应为：

这个式子的另一种解释为w的永久变化对y的影响。