空域高通滤波器
Posted sunlightheart
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了空域高通滤波器相关的知识,希望对你有一定的参考价值。
锐化处理的主要目的是突出灰度的过度部分,所以提取图像的边缘信息对图像的锐化来说非常重要。我们可以借助空间微分的定义来实现这一目的。定义图像的一阶微分的差分形式为
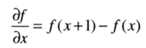
从定义中就可以看出图像一阶微分的结果在图像灰度变化缓慢的区域数值较小,而在图像灰度变化剧烈的区域数值较大,所以这一运算在一定程度可以反应图像灰度的变化情况。
对图像的一阶微分结果再次微分可以得到图像的二阶微分形式
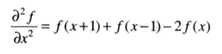
二阶微分可以反应图像像素变化率的变化,所以对灰度均匀变化的区域没有影响,而对灰度骤然变化的区域反应效果明显。
由于数字图像的边缘常常存在类似的斜坡过度,所以一阶微分时产生较粗的边缘,而二阶微分则会产生以零分开的双边缘,所以在增强细节方面二阶微分要比一阶微分效果好得多。
1.拉普拉斯算子
最简单的实现二阶微分的方法就是拉普拉斯算子,仿照一维二阶微分,二维图像的拉普拉斯算子其定义为
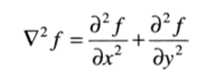
将前面提到的微分形式带入可以得到离散化的算子
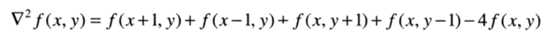
其对应的拉普拉斯模板为
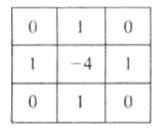
对角线方向也可以加入拉普拉斯算子,加入后算子模板变为
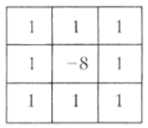
进行图像锐化时需要将拉普拉斯模板计算得的图像加到原图像当中,所以最终锐化公式为
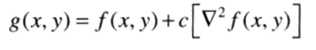
如果滤波器模板中心系数为负,则c值取负,反之亦然。这是因为当模板中心系数为负时,如果计算结果为正,则说明中间像素的灰度小于旁边像素的灰度,要想使中间像素更为突出,则需要则需要减小中间的像素值,即在原始图像中符号为正的计算结果。当计算结果为负时道理相同。
由上述原理就可以自定义拉普拉斯滤波器的计算函数了,该函数的输出为拉普拉斯算子对原图像的滤波,也就是提取的边缘信息。函数主体如下
import cv2 as cv import matplotlib.pyplot as plt import math import numpy as np original_image_test1 = cv.imread(‘test1.pgm‘,0) # 用原始图像减去拉普拉斯模板直接计算得到的边缘信息 def my_laplace_result_add(image, model): result = image - model for i in range(result.shape[0]): for j in range(result.shape[1]): if result[i][j] > 255: result[i][j] = 255 if result[i][j] < 0: result[i][j] = 0 return result def my_laplace_sharpen(image, my_type = ‘small‘): result = np.zeros(image.shape,dtype=np.int64) # 确定拉普拉斯模板的形式 if my_type == ‘small‘: my_model = np.array([[0, 1, 0], [1, -4, 1], [0, 1, 0]]) else: my_model = np.array([[1, 1, 1], [1, -8, 1], [1, 1, 1]]) # 计算每个像素点在经过高斯模板变换后的值 for i in range(image.shape[0]): for j in range(image.shape[1]): for ii in range(3): for jj in range(3): # 条件语句为判断模板对应的值是否超出边界 if (i+ii-1)<0 or (i+ii-1)>=image.shape[0]: pass elif (j+jj-1)<0 or (j+jj-1)>=image.shape[1]: pass else: result[i][j] += image[i+ii-1][j+jj-1] * my_model[ii][jj] return result # 将计算结果限制为正值 def my_show_edge(model): # 这里一定要用copy函数,不然会改变原来数组的值 mid_model = model.copy() for i in range(mid_model.shape[0]): for j in range(mid_model.shape[1]): if mid_model[i][j] < 0: mid_model[i][j] = 0 if mid_model[i][j] > 255: mid_model[i][j] = 255 return mid_model # 调用自定义函数 result = my_laplace_sharpen(original_image_test1, my_type=‘big‘) # 绘制结果 fig = plt.figure() fig.add_subplot(131) plt.title(‘original‘) plt.imshow(original_image_test1) fig.add_subplot(132) plt.title(‘edge‘) plt.imshow(my_show_edge(result)) fig.add_subplot(133) plt.title(‘sharpen‘) plt.imshow(my_laplace_result_add(original_image_test1,result)) plt.show()
程序运行得结果为
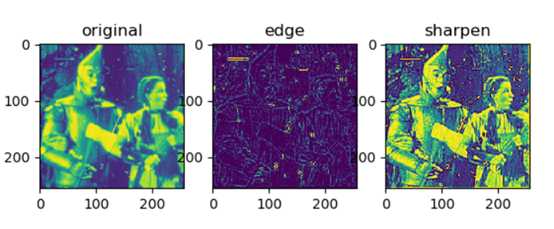
也可以调用cv2中的库函数进行拉普拉斯滤波,调用程序如下
import cv2 as cv from matplotlib import pyplot as plt # 用原始图像减去拉普拉斯模板直接计算得到的边缘信息 def my_laplace_result_add(image, model): result = image - model for i in range(result.shape[0]): for j in range(result.shape[1]): if result[i][j] > 255: result[i][j] = 255 if result[i][j] < 0: result[i][j] = 0 return result original_image_test1 = cv.imread(‘test1.pgm‘,0) # 函数中的参数ddepth为输出图像的深度,也就是每个像素点是多少位的。 # CV_16S表示16位有符号数 computer_result = cv.Laplacian(original_image_test1,ksize=3,ddepth=cv.CV_16S) plt.imshow(my_laplace_result_add(original_image_test1, computer_result)) plt.show()
运行结果如图
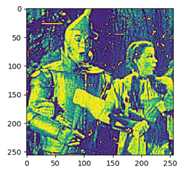
可以看出库函数的运行结果与自定义函数基本一致。
网络上由另外一种对拉普拉斯模板计算结果的处理方法,就是将计算结果取绝对值,再用源图像减去取绝对值的结果。用这种方式计算的程序为
import cv2 as cv import matplotlib.pyplot as plt import numpy as np original_image_test1 = cv.imread(‘test1.pgm‘,0) def my_laplace_result_add_abs(image, model): for i in range(model.shape[0]): for j in range(model.shape[1]): if model[i][j] < 0: model[i][j] = 0 if model[i][j] > 255: model[i][j] = 255 result = image - model for i in range(result.shape[0]): for j in range(result.shape[1]): if result[i][j] > 255: result[i][j] = 255 if result[i][j] < 0: result[i][j] = 0 return result # 调用自定义函数 result = my_laplace_sharpen(original_image_test1, my_type=‘big‘) # 绘制结果 fig = plt.figure() fig.add_subplot(121) plt.title(‘original‘) plt.imshow(original_image_test1) fig.add_subplot(122) plt.title(‘sharpen‘) plt.imshow(my_laplace_result_add_abs(original_image_test1,result)) plt.show()
运行结果为
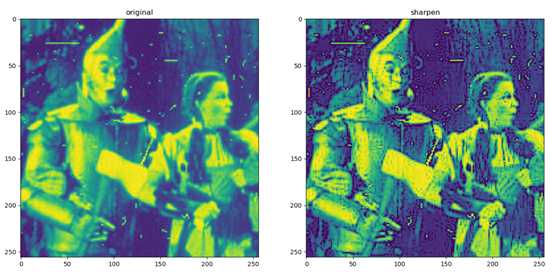
虽然这种算法机理不能确定正确,但是效果还可以。
2.非锐化掩蔽
除了通过二阶微分的形式提取到图像边缘信息,也可以通过原图像减去一个图像的非锐化版本来提取边缘信息,这就是非锐化掩蔽的原理,其处理过程为
- 将原图像进行模糊处理
- 用原图像减去模糊图像得到非锐化版本
- 将非锐化版本按照一定比例系数加到原图像中,得到锐化图像。
进行模糊处理时可以使用高斯滤波器等低通滤波器。非锐化掩蔽的自定义函数为
import cv2 as cv import matplotlib.pyplot as plt import numpy as np # 图像锐化函数 def my_not_sharpen(image, k, blur_size=(5, 5), blured_sigma=3): blured_image = cv.GaussianBlur(image, blur_size, blured_sigma) # model = image - blured_image # 注意不能直接用减法,对于图像格式结果为负时会自动加上256 model = np.zeros(image.shape, dtype=np.int64) for i in range(image.shape[0]): for j in range(image.shape[1]): model[i][j] = int(image[i][j]) - int(blured_image[i][j]) # 两个矩阵中有一个不是图像格式,则结果就不会转换为图像格式,如果不放心可以测试一下 sharpen_image = image + k * model # cv.convertScaleAbs计算公式为dst = uchar(|alpha*src+b|) 所以超过255的值会变成255,小于0的值会取绝对值 sharpen_image = cv.convertScaleAbs(sharpen_image) return sharpen_image # 提取图像边界信息函数 def my_get_model(image, blur_size=(5, 5), blured_sigma=3): blured_image = cv.GaussianBlur(image, blur_size, blured_sigma) model = np.zeros(image.shape, dtype=np.int64) for i in range(image.shape[0]): for j in range(image.shape[1]): model[i][j] = int(image[i][j]) - int(blured_image[i][j]) model = cv.convertScaleAbs(model) return model if __name__ == ‘__main__‘: ‘‘‘读取原始图片‘‘‘ original_image_test4 = cv.imread(‘test4.tif‘, 0) # 获得图像边界信息 edge_image_test4 = my_get_model(original_image_test4) # 获得锐化图像 sharpen_image_test4_3 = my_not_sharpen(original_image_test4, 3) # 显示结果 plt.subplot(131) plt.title(‘original‘) plt.imshow(original_image_test4) plt.subplot(132) plt.title(‘edge‘) plt.imshow(edge_image_test4) plt.subplot(133) plt.title(‘sharpen‘) plt.imshow(sharpen_image_test4_3) plt.show()
用自定义函数进行图像边界提取和图像增强的效果如下

3.梯度
图像处理的一阶微分使用梯度幅值来实现的,二元函数的梯度定义为
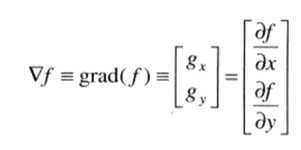
由于梯度是多维的,梯度本身并不能作为图像边缘的提取值,所以常用梯度的绝对值和或平方和作为幅度值来反应边缘情况。
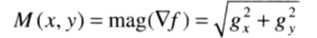
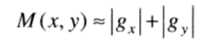
我们可以像前面拉普拉斯算子一样定义一个3×3模板的离散梯度形式
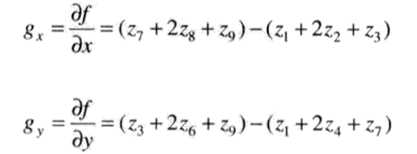
其对应的图像模板分别为
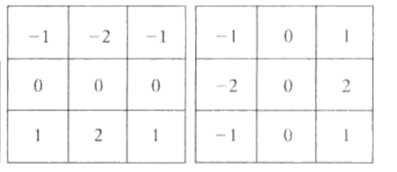
通过模板计算得到梯度值后,再将x、y方向的梯度绝对值相加或平方和相加,就得到了图像边缘的幅度值,再将提取到的幅度值图像加到原图像上,就得到了锐化后的图像。梯度方法的自定义函数为
import cv2 as cv import matplotlib.pyplot as plt import numpy as np # 输入图像,输出提取的边缘信息 def my_sobel_sharpen(image): result_x = np.zeros(image.shape,dtype=np.int64) result_y = np.zeros(image.shape, dtype=np.int64) result = np.zeros(image.shape, dtype=np.int64) # 确定拉普拉斯模板的形式 my_model_x = np.array([[-1, -2, -1], [0, 0, 0], [1, 2, 1]]) my_model_y = np.array([[-1, 0, 1], [-2, 0, 2], [-1, 0, 1]]) # 计算每个像素点在经过高斯模板变换后的值 for i in range(image.shape[0]): for j in range(image.shape[1]): for ii in range(3): for jj in range(3): # 条件语句为判断模板对应的值是否超出边界 if (i+ii-1)<0 or (i+ii-1)>=image.shape[0]: pass elif (j+jj-1)<0 or (j+jj-1)>=image.shape[1]: pass else: result_x[i][j] += image[i+ii-1][j+jj-1] * my_model_x[ii][jj] result_y[i][j] += image[i+ii-1][j+jj-1] * my_model_y[ii][jj] result[i][j] = abs(result_x[i][j]) + abs(result_y[i][j]) if result[i][j] > 255: result[i][j] = 255 return result # 将边缘信息按一定比例加到原始图像上 def my_result_add(image, model, k): result = image + k * model for i in range(result.shape[0]): for j in range(result.shape[1]): if result[i][j] > 255: result[i][j] = 255 if result[i][j] < 0: result[i][j] = 0 return result if __name__ == ‘__main__‘: ‘‘‘读取原始图片‘‘‘ original_image_test4 = cv.imread(‘test4.tif‘, 0) # 获得图像边界信息 edge_image_test4 = my_sobel_sharpen(original_image_test4) # 获得锐化图像 sharpen_image_test4 = my_result_add(original_image_test4, edge_image_test4, -0.5) # 显示结果 plt.subplot(131) plt.title(‘original‘) plt.imshow(original_image_test4) plt.subplot(132) plt.title(‘edge‘) plt.imshow(edge_image_test4) plt.subplot(133) plt.title(‘sharpen‘) plt.imshow(sharpen_image_test4) plt.show()
用梯度进行图像增强的效果为

4.Canny边缘检测
Canny算法是一个综合类的算法,它包含多个阶段,每个阶段基本上都可以用前面提到的方法实现。其具体流程如下 。
(1) 降低噪声
边缘检测很容易受噪声声的影响,所以在检测之前先做降噪处理是很有必要的。一般可以用5×5的高斯滤波器进行降噪处理。
(2) 寻找图像的强度梯度
然后对平滑后的图像进行水平方向和垂直方向的Sobel核滤波,得到水平方向(Gx)和垂直方向(Gy)的一阶导数。这两幅图像中,我们可以发现每个像素的边缘梯度和方向如下:
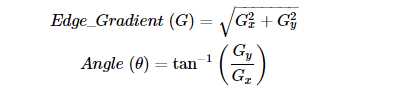
梯度方向总是垂直于边缘,它是四角之一,代表垂直、水平和两个对角线方向。
(3) 非极大抑制
得到梯度大小和方向后,对图像进行全面扫描,去除非边界点。在每个像素处,看这个点的梯度是不是周围具有相同梯 度方向的点中最大的最后的到的会是一个细边的边界。之后阈值
(4) 滞后阈值
现在要确定那些边界才是真正的边界,为此,我们需要两个阈值,minVal和maxVal。任何强度梯度大于maxVal的边都肯定是边,小于minVal的边肯定是非边,所以丢弃。位于这两个阈值之间的根据它们的连接性对边缘或非边缘进行分类(如果介于两者之间的话,就要看这个点是 否与某个被确定为真正的边界点相连,如果是就认为它也是边界点,如果不是就抛弃)
调用cv中canny库函数的程序示例
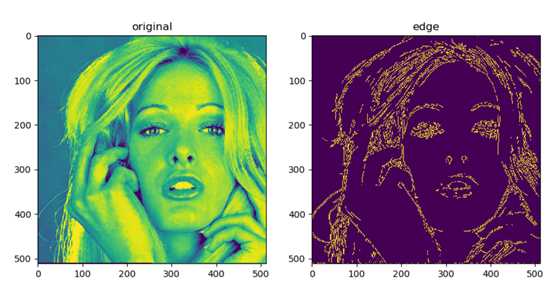
import cv2 as cv import matplotlib.pyplot as plt import numpy as np original_image_test4 = cv.imread(‘test2.tif‘, 0) # threshold为阈值,L2gradient为2范数,如果不指明则默认使用1范数 edge_image_test4 = cv.Canny(original_image_test4, threshold1=100, threshold2=200, L2gradient=0) plt.subplot(121) plt.title(‘original‘) plt.imshow(original_image_test4) plt.subplot(122) plt.title(‘edge‘) plt.imshow(edge_image_test4) plt.show()
效果如下
以上是关于空域高通滤波器的主要内容,如果未能解决你的问题,请参考以下文章