二叉搜索树

Posted 2020-08-14 小困

• 树数据结构

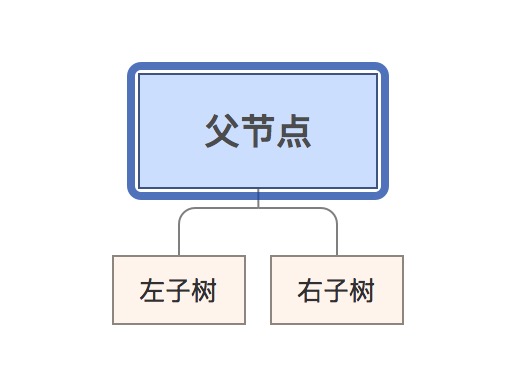
　　　　树是一种二位数据结构，并且非常常见。树的元素，叶节点有两个“指针”和数据域。

• 二叉排序树

　　　　在一个子树中，根节点比左子节点要大，比右子节点要小。

• 树的遍历

　　　　先序遍历：先遍历子树的根节点，再遍历左子节点，最后遍历右子节点。

　　　　中序遍历：先遍历左子节点，再遍历根节点，最后遍历右子节点。

　　　　后序遍历：先遍历左子节点，再遍历右子节点，最后遍历根节点。

　　　　　　　　　　　　　　　　　　

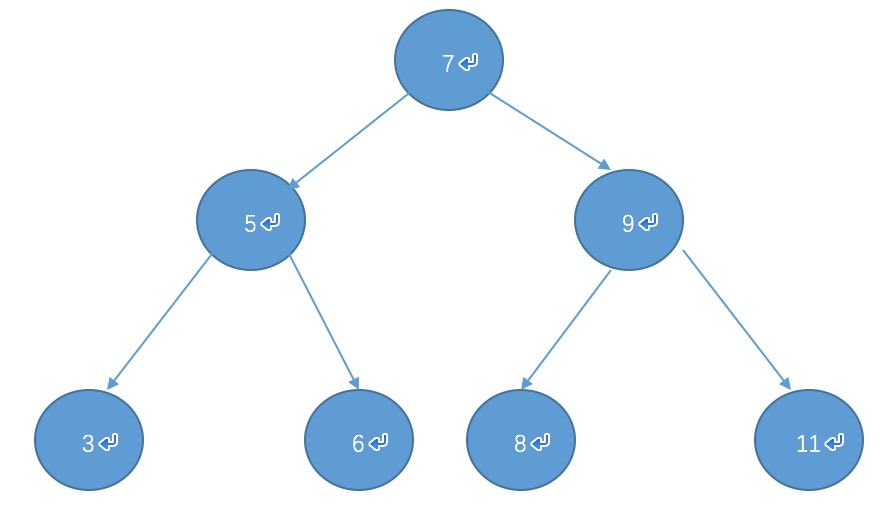
• 例子

　　　　添加节点的方法就是用两个节点，一个记录父节点，一个记录行进节点。

　　　　如果进入数据大于根节点，则进入右节点，如果小于根节点，则进入左节点。

　　　　

　　

package tree;
/**
 * 二叉排序树
 * @author MacBook
 *
 */
public class tree1 {
    private treeNode root;
    public treeNode getRoot(){
        return root;
    }
    public void insertNode(treeNode n){
        treeNode parent = root;
        treeNode son = root;
        if(root == null){
            root = n;
            return;
        }
        while(son != null){
            parent = son;
            if(n.getData()>son.getData())
                son = son.getRight();
            else
                son = son.getLeft();
        }
        if(parent.getData()>n.getData())
            parent.setLeft(n);
        else 
            parent.setRight(n);
    }
    //前序遍历
    public void print1(treeNode n){
        if(n!=null)
        {
            System.out.println(n.getData());
            print1(n.getLeft());
            print1(n.getRight());
            
        }
    }
    //中序遍历
    public void print2(treeNode n){
        if(n!=null)
        {
            print2(n.getLeft());
            System.out.println(n.getData());
            print2(n.getRight());
        }
    }

    //后序遍历
    public void print3(treeNode n){
        if(n!=null)
        {
            print3(n.getLeft());
            print3(n.getRight());
            System.out.println(n.getData());
        }
    }

    public static void main(String[] args) {
        tree1 t = new tree1();
        treeNode n1 = new treeNode();
        n1.setData(7);
        treeNode n2 = new treeNode();
        n2.setData(5);
        treeNode n3 = new treeNode();
        n3.setData(9);
        treeNode n4 = new treeNode();
        n4.setData(3);
        treeNode n5 = new treeNode();
        n5.setData(6);
        treeNode n6 = new treeNode();
        n6.setData(11);
        treeNode n7 = new treeNode();
        n7.setData(8);
        t.insertNode(n1);
        t.insertNode(n2);
        t.insertNode(n3);
        t.insertNode(n4);
        t.insertNode(n5);
        t.insertNode(n6);
        t.insertNode(n7);
        t.print3(t.getRoot());
    }
}
class treeNode{
    private int data;
    private treeNode left;
    private treeNode right;
    public int getData() {
        return data;
    }
    public void setData(int data) {
        this.data = data;
    }
    public treeNode getLeft() {
        return left;
    }
    public void setLeft(treeNode left) {
        this.left = left;
    }
    public treeNode getRight() {
        return right;
    }
    public void setRight(treeNode right) {
        this.right = right;
    }
    
}

　　　　先序遍历结果：7 5 3 6 9 8 11

　　　　中序遍历结果：3 5 6 7 8 9 11

　　　　后序遍历结果：3 6 5 8 11 9 7

• 层序遍历

　　　　这个遍历方法要求，遍历的时候是逐层输出的，这个时候需要用到一个队列数据结构，将父节点入队列，处于队列首部的节点出队列的时候，输出它的值并把它两个子节点放入队列，先左后右。利用队列先进先出的特性，可以把树逐层遍历。

　　　　下面是队列的定义；

//队列
class queue{
    private queueNode first;
    private queueNode end;
    public queue(){
        first = end = null;
    }
    //如队列
    public void InQueue(queueNode n){
        if(first == null && end == null)
            first = end = n;
        else{
            end.setNext(n);
            n.setNext(null);
            end = n;
        }
    }
    //出队列
    public queueNode OutQueue(){
        if(first == null && end ==null)
            return null;
        else if(first == end && first != null && end != null)
        {
            queueNode p = first;
            first = end = null;
            return p;
        }
        else{
            queueNode p = first;
            first = first.getNext();
            return p;
        }
        
    }
    //打印数据结构
    public void printQueue(){
        queueNode pNode = first;
        while(pNode != null)
        {
            System.out.print(pNode.getData()+" ");
            pNode = pNode.getNext();
        }
        System.out.println();
    }
    //是否为空
    public boolean isEmtpy(){
        if(first == null && end == null)
            return true;
        else
            return false;
    }
}
//队列节点
class queueNode{
    private queueNode next;
    private Object data;
    public queueNode getNext() {
        return next;
    }
    public void setNext(queueNode next) {
        this.next = next;
    }
    public Object getData() {
        return data;
    }
    public void setData(Object data) {
        this.data = data;
    }
    
}

　　　　层序遍历的设计方法；

//层序遍历
    public void print4(treeNode n){
        queue queue = new queue();
        queueNode qNode = new queueNode();
        qNode.setData(n);
        queue.InQueue(qNode);
        
        while(!queue.isEmtpy()){
            queueNode node = queue.OutQueue();
            treeNode temp = (treeNode)node.getData();
            System.out.println(temp.getData());
            if(temp.getLeft() != null)
            {
                queueNode inData = new queueNode();
                inData.setData(temp.getLeft());
                queue.InQueue(inData);
            }
            if(temp.getRight() != null)
            {
                queueNode inData = new queueNode();
                inData.setData(temp.getRight());
                queue.InQueue(inData);
            }
            
        }
        
    }

• 获得树的最大深度

    // 获得树的深度
    public int getDepth(treeNode n) {
        if (n == null)
            return 0;
        else {
            int left = getDepth(n.getLeft());
            int right = getDepth(n.getRight());
            return (left > right) ? (left + 1) : (right + 1);
        }
    }

• 转换为双向链表

　　　　通过改变左右孩子的指向变换为有序双向链表。中序遍历的顺序是：左，父，右；因为子树中左节点<父节点<右节点，所以中序遍历必然是升序的序列。通过中序遍历，改变左子节点为链表上一节点，右子节点为链表下一节点，并保存当前构建的链表节点，通过递归的方式重新构建树。

    // 转换成双向链表
    public treeNode ConverseToList(treeNode root, treeNode listend) {
        if (root == null)
            return listend;
        treeNode current = root;
        if (current.getLeft() != null)
            listend = ConverseToList(current.getLeft(), listend);
        current.setLeft(listend);
        if (listend != null)
            listend.setRight(current);
        listend = current;
        if (current.getRight() != null)
            listend = ConverseToList(current.getRight(), listend);
        return listend;
    }

• 返回低k层存在的节点数

    //返回第k层的节点数目
    public int getNumbers(treeNode root,int k){
        if(k == 0 || root == null)
            return 0;
        if(k == 1)
            return 1;
        else{
            int left = getNumbers(root.getLeft(),k-1);
            int right = getNumbers(root.getRight(), k-1);
            return left + right;
        }
        
            
    }

• 计算叶子节点的数目

    //返回叶子节点的数目
    public int getSonNumbers(treeNode root){
        if(root == null)
            return 0;
        else if(root.getLeft() == null && root.getRight() == null)
            return 1;
        else{
            int left = getSonNumbers(root.getLeft());
            int right = getSonNumbers(root.getRight());
            return left + right;
        }
    }

• 判断树是否为平衡树

　　　　平衡树（AVL）的概念就是左子树的高度和右子树的高度相差不超过1。

    //判断树是否平衡
    public boolean isAVL(treeNode root){
        int left = depth(root.getLeft());
        int right = depth(root.getRight());
        System.out.println("left="+left+" right="+right);
        if(Math.abs(left-right)>1)
            return false;
        else
            return true;
    }
    public int depth(treeNode root){
        if(root == null)
            return 0;
        else{
            int left = depth(root.getLeft());
            int right = depth(root.getRight());
            return (left>right)?(left+1):(right+1);
        }
    }

• 反转二叉树

　　　　反转二叉树，就是左节点变为右节点。而前序遍历的顺序很适合去做反转，因为前序遍历是先遍历父节点。

    //反转二叉树 
    public void reverseTree(treeNode root){
        if(root == null)
            return ;
        treeNode left = root.getLeft();
        treeNode right = root.getRight();
        root.setLeft(right);
        root.setRight(left);
        reverseTree(root.getLeft());
        reverseTree(root.getRight());
    }

• 求两个子节点最早的公共父节点

　　　　首先有个从当前节点往下找子节点的方法，如果两个子节点同为左子树，则左子树进入下一状态，若同为右子树，则右子树进入下一状态。若一左一右，说明当前节点为最早公共父节点。

//求两个节点的最早公共父节点
    public treeNode findFather(treeNode root,treeNode n1,treeNode n2){
        treeNode current = root;
        while(true){
            boolean n1Left = findNode(current.getLeft(),n1);
            boolean n1right = findNode(current.getRight(), n1);
            boolean n2Left = findNode(current.getLeft(),n2);
            boolean n2right = findNode(current.getRight(), n2);
            if(n1Left && n2Left)
                current = current.getLeft();
            else if(n1right && n2right)
                current = current.getRight();
            else {
                break;
            }
        }
        return current;
    }
    //寻找节点
    public boolean findNode(treeNode root,treeNode node){
        if(root == node){
            return true;
        }else if(root == null || node == null)
            return false;
        boolean found = findNode(root.getLeft(),node);
        if(!found)
            found = findNode(root.getRight(),node);
        return found;
        
    }