代码随想录Day20-Leetcode654.最大二叉树，617.合并二叉树，700.二叉搜索树中的搜索，98.验证二叉搜索树

Posted 2023-04-04 herbert118

654.最大二叉树

题目链接:https://leetcode.cn/problems/maximum-binary-tree/
基本的模拟思路很快

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) 
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * 
 */
/**
 * @param number[] nums
 * @return TreeNode
 */
 //完了,漏了一天没写立刻没思路了,这就是基础的重要性
var constructMaximumBinaryTree = function(nums) 
    return consTree(nums,0,nums.length-1)
;
/**
 * @param number[] arr
 * @return TreeNode
 */
function consTree(arr,left,right)
    if(left>right)
        return null
    
    let maxIndex = left;
    let max = arr[left]
    for(let i = left+1; i<= right;i++)
        if(arr[i]>max)
            max = arr[i]
            maxIndex = i
        
    
    let node = new ListNode(max)

    node.left = consTree(arr,left,maxIndex-1)
    node.right = consTree(arr,maxIndex+1,right)
    return node

617.合并二叉树

题目链接:https://leetcode.cn/problems/merge-two-binary-trees/
很明显的递归写法,不过效率好低,10%不到;

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) 
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * 
 */
/**
 * @param TreeNode root1
 * @param TreeNode root2
 * @return TreeNode
 */
var mergeTrees = function(root1, root2) 
    if(root1==null)
        return root2
    else if(root2 == null)
        return root1
    else
        root1.val = root1.val + root2.val
        root1.left = mergeTrees(root1.left,root2.left)
        root1.right = mergeTrees(root1.right,root2.right)
        return root1
    
;

另外好像有bfs的方法,暂略

700.二叉搜索树中的搜索

递归

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) 
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * 
 */
/**
 * @param TreeNode root
 * @param number val
 * @return TreeNode
 */
var searchBST = function(root, val) 
    if(root == null)
        return null
    
    if(val==root.val)
        return root
    else if (val>root.val)
        return searchBST(root.right,val) 
    else
        return searchBST(root.left,val)
    
;

//又犯了经典错误:递归少参数

迭代
不知道怎么回事,力扣上迭代总比递归慢...

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) 
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * 
 */
/**
 * @param TreeNode root
 * @param number val
 * @return TreeNode
 */
var searchBST = function(root, val) 
    let node = root
    while(node!=null)
        if(node.val == val)
            return node
        else if(val>node.val)
            node = node.right
        else
            node = node.left
        
    
    return null
;

98.验证二叉搜索树

用了中序遍历然后投影;
不太清楚怎么递归,感觉子问题不好划分,左右子树都有效的情况下,该树仍可能会无效

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) 
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * 
 */
/**
 * @param TreeNode root
 * @return boolean
 */
 //似乎这个结构并不那么递归?左右子树都有效的情况下,可能会无效
 //类似于局部有序不等于整体有序;
 //暴力的方法是,直接中序遍历投影,检查是否有序
var isValidBST = function(root) 
    let arr = []
    inOrder(root,arr)
    for(let i =1;i<arr.length;i++)
        if(arr[i]<=arr[i-1])
            return false
        
    
    return true
;

function inOrder(node,result)
    if(node == null)
        return
    
    inOrder(node.left,result)
    result.push(node.val)
    inOrder(node.right,result)

看了题解后,发现递归需要设置界限,而非根结点和左右孩子结点比大小

代码随想录day 31 455.分发饼干 | 376. 摆动序列 | 53. 最大子序和

455.分发饼干

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。

对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

示例 1:

• 输入: g = [1,2,3], s = [1,1]
• 输出: 1 解释:你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,2,3。虽然你有两块小饼干，由于他们的尺寸都是1，你只能让胃口值是1的孩子满足。所以你应该输出1。

这里的局部最优就是大饼干喂给胃口大的，充分利用饼干尺寸喂饱一个，全局最优就是喂饱尽可能多的小孩。

可以尝试使用贪心策略，先将饼干数组和小孩数组排序。

然后从后向前遍历小孩数组，用大饼干优先满足胃口大的，并统计满足小孩数量。

class Solution 
    public int findContentChildren(int[] g, int[] s) 
        Arrays.sort(g);
        Arrays.sort(s);
        int start = 0;
        int cnt = 0;
        for (int i = 0; i < s.length && start < g.length; i++) 
            if (s[i] >= g[start]) 
                start++;
                cnt++;
            
        
        return cnt;
    

376. 摆动序列

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为摆动序列。第一个差（如果存在的话）可能是正数或负数。少于两个元素的序列也是摆动序列。

例如， [1,7,4,9,2,5] 是一个摆动序列，因为差值 (6,-3,5,-7,3) 是正负交替出现的。相反, [1,4,7,2,5] 和 [1,7,4,5,5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。

给定一个整数序列，返回作为摆动序列的最长子序列的长度。 通过从原始序列中删除一些（也可以不删除）元素来获得子序列，剩下的元素保持其原始顺序。

示例 1:

• 输入: [1,7,4,9,2,5]
• 输出: 6
• 解释: 整个序列均为摆动序列。

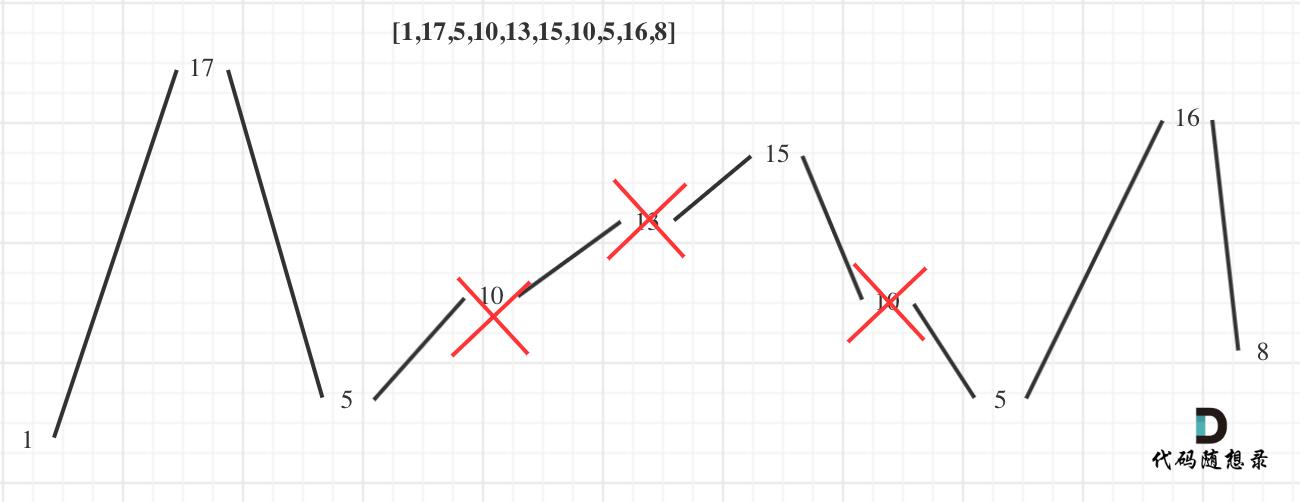
局部最优：删除单调坡度上的节点（不包括单调坡度两端的节点），那么这个坡度就可以有两个局部峰值。

整体最优：整个序列有最多的局部峰值，从而达到最长摆动序列。

class Solution 
    public int wiggleMaxLength(int[] nums) 
        if (nums.length <= 1) return nums.length;
        int curDiff = 0;
        int preDiff = 0;
        int cnt = 1;

        for (int i = 1; i < nums.length; i++) 
            curDiff = nums[i] - nums[i - 1];
            if ((curDiff > 0 && preDiff <= 0) || (curDiff < 0 && preDiff >= 0)) 
                cnt++;
                preDiff = curDiff;
            
        
        return cnt;
    

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例:

• 输入: [-2,1,-3,4,-1,2,1,-5,4]
• 输出: 6
• 解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

 

class Solution 
    public int maxSubArray(int[] nums) 
        if (nums.length == 1) return nums[0];
        int sum = Integer.MIN_VALUE;
        int cnt = 0;
        for (int i = 0; i < nums.length; i++) 
            cnt += nums[i];
            sum = Math.max(sum, cnt);
            if (cnt <= 0) 
                cnt = 0;
            
        
        return sum;