c++:二叉搜索树BinarySortTree

Posted 2021-07-17 You are my ghost

文章目录

• 二叉搜索树BinarySortTree
• • 1.二叉搜索树概念
  • 2.二叉搜索树操作
  • • （1）查找
    • （2）插入节点
    • （3）删除节点
  • 3.二叉搜索树的代码实现
  • • （1）功能实现
    • （2）测试
  • 2.4 二叉搜索树的应用
  • • 1. K模型
    • 2. KV模型
    • 3.KV模型的代码实现
    • • （1）功能实现
      • （2）测试

二叉搜索树BinarySortTree

1.二叉搜索树概念

二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:
若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
若它的右子树不为空，则右子树上所有节点的值都大于根节点的值

它的左右子树也分别为二叉搜索树
如图所示

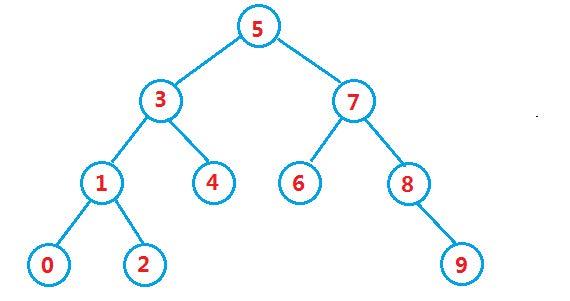
二叉搜索树最大的功能便是搜索；一般来讲它比顺序表以链表的搜索时间复杂度要低；但是在极端条件下，它和顺序表、链表的时间复杂度相同。
当是满二叉树时，若搜索一个值，最多只需要二叉树的层数次；时间复杂度O(logN)。

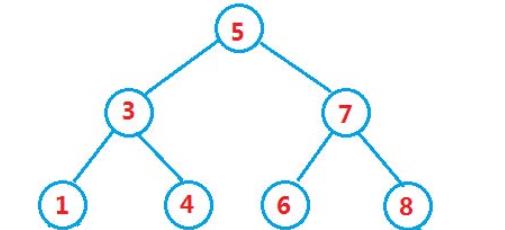
当二叉树为下图结构时，若找“9”，便要遍历所有节点，时间复杂度最大，为O(N)。

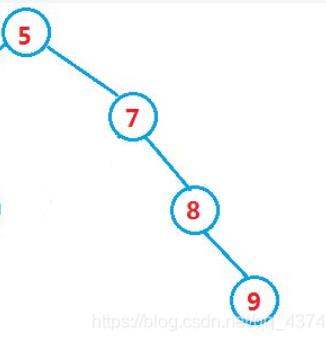
2.二叉搜索树操作

（1）查找

（2）插入节点

插入的具体过程如下：
a. 树为空，则直接插入

b. 树不空，按二叉搜索树性质查找插入位置，插入新节点
从根节点开始，若插入的值小于根节点，便让根节点的左孩子成为新的父亲；若插入的值大于根节点，便让根节点的右孩子成为新的父亲；以此类推，直到正确的插入数据。

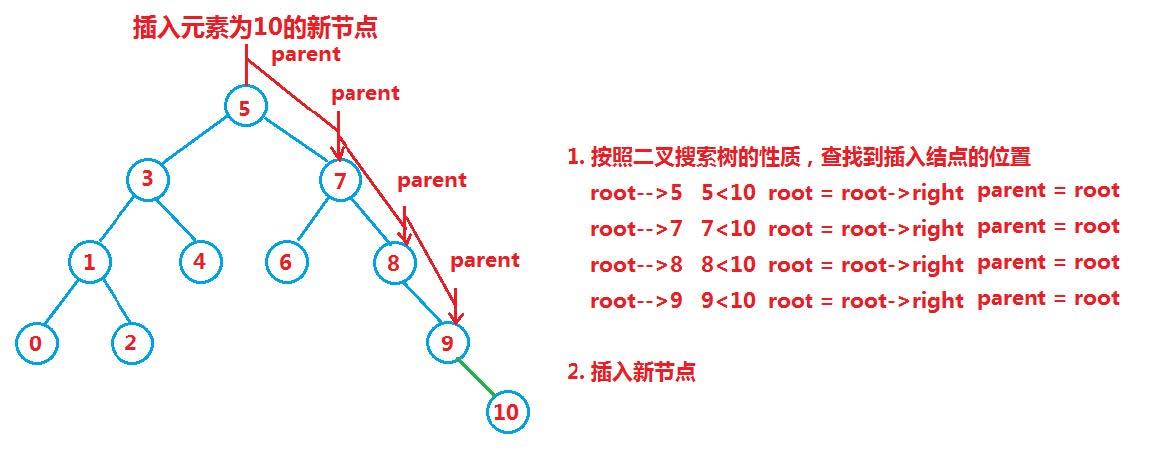
（3）删除节点

首先查找元素是否在二叉搜索树中，如果不存在，则返回, 否则要删除的结点可能分下面四种情况：
a. 要删除的结点无孩子结点：删除后使其父亲节点指向nullptr；
b. 要删除的结点只有左孩子结点：删除后使其父亲结点指向其右孩子结点；
c. 要删除的结点只有右孩子结点：删除后使其父亲结点指向其左孩子结点；
d. 要删除的结点有左、右孩子结点：在它的右子树中寻找中序下的第一个结点(关键码最小)，用它的值填补到被删除节点中;然后对右子树中序下的第一个结点进行删除。
看起来有待删除节点有4中情况，实际情况a可以与情况b或者c合并起来，因此真正的删除过程如下：

3.二叉搜索树的代码实现

（1）功能实现

#pragma once
#include<iostream>
#include<vector>
using namespace std;

template<class K>
struct BSTNode 
{
	K _key;//所存储的数据
	struct BSTNode<K>* _left;
	struct BSTNode<K>* _right;
	BSTNode(const K& key)
		:_key(key)
		,_left(nullptr)
		,_right(nullptr)
	{}
};

template<class K>
class BSTree
{
	typedef BSTNode<K> Node;
private:
	Node* _root = nullptr;
public:
	//遍历
	void InOrder(Node* root)
	{
		if (root == nullptr)
		{
			return;
		}
		//中序遍历
		InOrder(root->_left);
		cout << root->_key << " ";
		InOrder(root->_right);
	}
	//重载一个无参函数，方便接口使用
	void InOrder()
	{
		InOrder(_root); 
		cout << endl;
	}
	//插入
	bool Insert(const K& key)
	{
		if (_root == nullptr)
		{
			_root = new Node(key);
		}
		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{
			parent = cur;
			if (key > cur->_key)
			{
				cur = cur->_right;
			}
			else if (key < cur->_key)
			{
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}
		cur = new Node(key);
		if (key > parent->_key)
		{
			parent->_right = cur;
		}
		else 
		{
			parent->_left = cur;
		}
	}
	//查找
	Node* Find(const K& key)
	{
		cout << "WANT FIND:" << key << endl;
		Node* cur = _root;
		while (cur)
		{
			if (key > cur->_key)
			{
				cur = cur->_right;
			}
			else if (key < cur->_key)
			{
				cur = cur->_left;
			}
			else
			{
				return cur;
			}
		}
		cout << "NOT FIND" << endl;
		return nullptr;
	}
	//删除节点
	bool Erase(const K& key)
	{
		cout << "ERASE:" << key << endl;
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (key > cur->_key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (key < cur->_key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				//找到了，准备删除该节点
				//左为空||左右均为空结合讨论
				if (cur->_left == nullptr)
				{
					if (cur == _root)
						_root = cur->_right;
					else
					{
						if (cur == parent->_left)
							parent->_left = cur->_right;
						else
							parent->_right = cur->_right;
					}
					delete cur;
				}
				else if (cur->_right == nullptr)
				{
					if (cur == _root)
						_root = cur->_left;
					else
					{
						if (cur == parent->_left)
							parent->_left = cur->_left;
						else
							parent->_right = cur->_left;
					}
					delete cur;
				}
				else
				{
					//subMin的父亲节点
					Node* subMinParent = cur;
					//右子树中寻找中序下的第一个节点subMin
					Node* subMin = cur->_right;
					while (subMin->_left)
					{
						subMinParent = subMin;
						subMin = subMin->_right;
					}
					cur->_key = subMin->_key;
					//subMin左孩子一定为空
					//考虑subMinParent可能为要删除的节点
					if (subMin == subMinParent->_left)
					{
						subMinParent->_left = subMin->_right;
					}
					else
					{
						subMinParent->_right = subMin->_right;
					}
					delete subMin;
				}
				return true;
			}
		}
		cout << "ERASE ERROR" << endl;
		return false;
	}
};

（2）测试

#include "BSTree.h"
using namespace std;
void BSTreeTest1()
{
	//插入节点
	BSTree<int> i;
	i.Insert(5);
	i.Insert(6);
	i.Insert(7);
	i.Insert(8);
	i.Insert(4);
	i.Insert(3);
	i.Insert(2);
	i.Insert(1);
	i.Insert(9);
	i.InOrder();
	cout << endl;
	//寻找节点
	BSTNode<int>* ret1 = i.Find(6);
	if (ret1)
	{
		cout << "FIND IT!" << endl;
	}
	BSTNode<int>* ret2 = i.Find(0);
	if (ret2)
	{
		cout << "FIND IT!" << endl;
	}
	cout << endl;

	//删除节点
	i.Erase(0);
	i.Erase(5);
	i.Erase(1);
	i.Erase(9);
	i.InOrder();
}

int main()
{
	BSTreeTest1();
	return 0;
}

运行截图

2.4 二叉搜索树的应用

1. K模型

即为上述代码所实现的模型

功能：
a.查找在不在；
b.排序&&去重

K模型即只有Key作为关键码;节点结构中只需要存储Key即可，Key即为需要搜索到的值。
比如：给一个单词word，判断该单词是否拼写正确，具体方式如下：
以单词集合中的每个单词作为key，构建一棵二叉搜索树在二叉搜索树中检索该单词是否存在，存在则拼写正确，不存在则拼写错误。

2. KV模型

每一个关键码key，都有与之对应的值Value;即<Key, Value>的键值对。

功能：
a.查找在不在；
b.排序&&去重
c.通过key查找value：比如字典
d.统计次数

比如英汉词典就是英文与中文的对应关系，通过英文可以快速找到与其对应的中文，英文单词与其对应的中文<word, chinese>就构成一种键值对。

实现一个简单的英汉词典dict，可以通过英文找到与其对应的中文，具体实现方式如下：
<word, chinese>为键值对构造二叉搜索树，查询英文单词时，只需给出英文单词，就可快速找到与其对应的中文。

3.KV模型的代码实现

代码逻辑完全相同，只需要添加一个新的值value，与key形成键值对

（1）功能实现

#pragma once
#pragma once
#include<iostream>
#include<vector>
using namespace std;

template<class K, class V>
struct BSTNodeKV
{
	const K _key;//所存储的数据
	V _value;
	struct BSTNodeKV<K, V>* _left;
	struct BSTNodeKV<K, V>* _right;
	BSTNodeKV(const K& key, const V& value)
		:_key(key)
		, _value(value)
		, _left(nullptr)
		, _right(nullptr)
	{}
};

template<class K, class V>
class BSTreeKV
{
	typedef BSTNodeKV<K, V> Node;
private:
	Node* _root = nullptr;
public:
	//遍历
	void InOrder(Node* root)
	{
		if (root == nullptr)
		{
			return;
		}
		//中序遍历
		InOrder(root->_left);
		cout << root->_key << ":"<<root->_value<<" ";
		InOrder(root->_right);
	}
	//重载一个无参函数，方便接口使用
	void InOrder()
	{
		InOrder(_root);
		cout << endl;
	}
	//插入
	bool Insert(const K& key, const V& value)
	{
		if (_root == nullptr)
		{
			_root = new Node(key, value);
		}
		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{
			parent = cur;
			if (key > cur->_key)
			{
				cur = cur->_right;
			}
			else if (key < cur->_key)
			{
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}
		cur = new Node(key, value);
		if (key > parent->_key)
		{
			parent->_right = cur;
		}
		else
		{
			parent->_left = cur;
		}
	}
	//查找
	Node* Find(const K& key, const V& value)
	{
		//cout << "WANT FIND:" << key << endl;
		Node* cur = _root;
		while (cur)
		{
			if (key > cur->_key)
			{
				cur = cur->_right;
			}
			else if (key < cur->_key)
			{
				cur = cur->_left;
			}
			else
			{
				return cur;
			}
		}
		//cout << "NOT FIND" << endl;
		return nullptr;
	}
	//删除节点
	bool Erase(const K& key, const V& value)
	{
		cout << "ERASE:" << key << endl;
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (key > cur->_key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (key < cur->_key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				//找到了，准备删除该节点
				//左为空||左右均为空结合讨论
				if (cur->_left == nullptr)
				{
					if (cur == _root)
						_root = cur->_right;
					else
					{
						if (cur == parent->_left)
							parent->_left = cur->_right;
						else
							parent->_right = cur->_right;
					}
					delete cur;
				}
				else if (cur->_right == nullptr)
				{
					if (cur == _root)
						_root = cur->_left;
					else
					{
						if (cur == parent->_left)
							parent->_left = cur->_left;
						else
							parent->_right = cur->_left;
					}
					delete cur;
				}
				else
				{
					//subMin的父亲节点
					Node* subMinParent = cur;
					//右子树中寻找中序下的第一个节点subMin
					Node* subMin = cur->_right;
					while (subMin->_left)
					{
						subMinParent = subMin;
						subMin = subMin->_right;
					}
					cur->_key = subMin->_key;
					//subMin左孩子一定为空
					//考虑subMinParent可能为要删除的节点
					if (subMin == subMinParent->_left)
					{
						subMinParent->_left = subMin->_right;
					}
					else
					{
						subMinParent->_right = subMin->_right;
					}
					delete subMin;
				}
				return true;
			}
		}
		cout << "ERASE ERROR" << endl;
		return false;
	}
	//通过key来找value
	V FindValue(const K& key)
	{
		cout << "WANT FIND:" << key <<":";
		Node* cur = _root;
		while (cur)
		{
			if (key > cur->_key)
			{
				cur = cur->_right;
			}
			else if (key < cur->_key)
			{
				cur = cur->_left;
			}
			else
			{
				return cur->_value;
			}
		}
		cout << "NOT FIND" << endl;
		exit(1);
	}
};

void BSTreeKVTest()
{
	BSTreeKV<string, string> dict;
	dict.Insert("banana", "香蕉");
	dict.Insert("ciname", "电影");
	dict.Insert("apple", "苹果");
	dict.Insert("dog", "狗");
	dict.Insert("string", "字符串");
	dict.Insert("sort", "排序");
	dict.InOrder();
	
	cout << dict.FindValue("sort") << endl;
	cout << dict.FindValue二叉搜索树(BST)---python实现

 python实现二叉搜索树_二叉搜索树(BST)---python实现
 数据结构——二叉搜索树B树B-树
 数据结构与算法笔记（十六）—— 二叉搜索树
 Java 大话数据结构(11) 查找算法（二叉排序树/二叉搜索树）
 BST(二叉搜索树),AVL(平衡二叉树)RBT(红黑树)的区别