概率论与数理统计猴博士 笔记 p21-23 二维连续型求边缘分布函数和密度函数,已知两个边缘密度函数求f(x,y)
Posted karshey
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了概率论与数理统计猴博士 笔记 p21-23 二维连续型求边缘分布函数和密度函数,已知两个边缘密度函数求f(x,y)相关的知识,希望对你有一定的参考价值。
二维连续型求边缘分布函数
题型如下:给出F(x,y),让我们求F(x),F(y)

步骤:
F
X
(
x
)
=
F
(
x
,
+
∞
)
F
Y
(
y
)
=
F
(
+
∞
,
y
)
F_X(x)=F(x,+∞) \\\\F_Y(y)=F(+∞,y)
FX(x)=F(x,+∞)FY(y)=F(+∞,y)
直接做上面那道例题:

二维连续型求边缘密度函数
题干:给出F(x,y),让我们求f(x),f(y)

方法:
f
X
(
x
)
=
∫
−
∞
+
∞
f
(
x
,
y
)
d
y
f
Y
(
y
)
=
∫
−
∞
+
∞
f
(
x
,
y
)
d
x
f_X(x)=\\displaystyle \\int^+∞_-∞f(x,y)dy \\\\f_Y(y)=\\displaystyle \\int^+∞_-∞f(x,y)dx
fX(x)=∫−∞+∞f(x,y)dyfY(y)=∫−∞+∞f(x,y)dx
步骤:

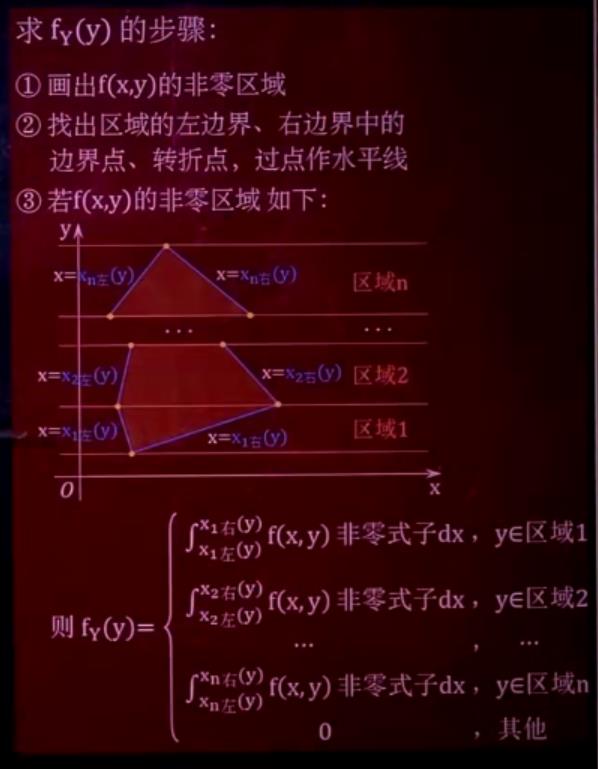
我们以例1为例做一下:
第一步:

第二步:
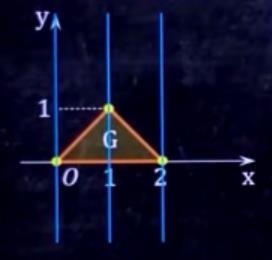
第三步:**因为是求f(x),所以要作垂直于x轴的线。**最左边的蓝线和最右边的蓝线中间有几个格,公式里就会有几个区域。
这道题有两个区域。每个区域的积分上限是上边界的表达式,下限是下边界的表达式。这里是求f(x),所以是对x的表达式。
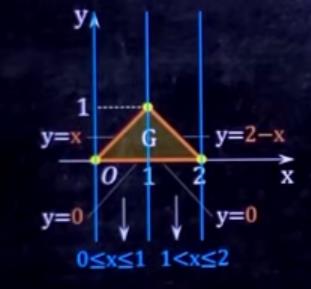

然后得出答案:

求f(y)同理:
要作垂直于y轴的线
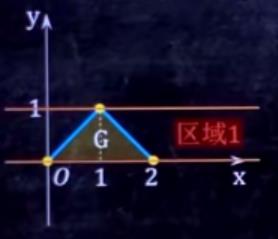
y的范围是区间。积分上限是右边线的y的表达式,下限是左边线的y的表达式。


答案:

接下来尝试自己做例2:

解:
对x:


对y:

已知两个边缘密度函数求f(x,y)
其实就是已知f(x),f(y)来求f(x,y)。
如题:
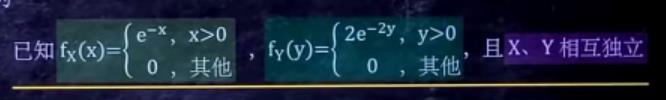
步骤:
把f(x),f(y)不为0的表达式相乘,范围加在一起即可(相互独立,可以同时满足)
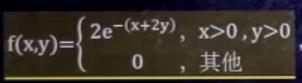
以上是关于概率论与数理统计猴博士 笔记 p21-23 二维连续型求边缘分布函数和密度函数,已知两个边缘密度函数求f(x,y)的主要内容,如果未能解决你的问题,请参考以下文章
概率论与数理统计猴博士 笔记 p26-28 Ff的性质一二维连续型求期望方差
概率论与数理统计猴博士 笔记 p11-14 一维二维离散型求分布函数和期望方差
概率论与数理统计猴博士 笔记 p8-10 一维二维离散型求分布律二维离散型求边缘分布律
概率论与数理统计猴博士 笔记 p17-20 一二维连续型:已知F,求f;已知f,求f