概率论与数理统计猴博士 笔记 p29-32 均匀分布泊松分布指数分布几何分布

Posted 2022-04-18 karshey

均匀分布U

题型：已知某随机变量满足某分布，求对应的概率，期望，方差。

也是套公式：
例1：
设随机变量X~U[2,5]，求PX>=4、EX、DX。
套公式得：
$$\begin{gathered} px\ge 4=\frac{1}{3} \\ EX=\frac{7}{2} \\ DX=\frac{3}{4} \end{gathered}$$

例2：
设随机变量K在区间(1,6)上服从均匀分布，则方程x²+kx+1=0有实根的概率是__。

解：
$$\frac{4}{5}$$

例3：
设二维随机变量(X,Y)在区域G=(x,y)|x≥0,y ≥0,x+y≤1上服从均匀分布,求PX+Y<=1/2

解：
$$\frac{1}{4}$$

泊松分布P

例1：
设随机变量X~P(5)，求PX=2、EX、DX。

$$\begin{gathered} PX=2=\frac{25}{2}{e}^{-5} \\ EX=5 \\ DX=5 \end{gathered}$$

例2：某电话交换台每分钟接到的呼叫数X，服从参数为5的泊松分布，求在一分钟内呼叫数X为2次的概率。

解：
$$PX=2=\frac{25}{2}{e}^{-5}$$

例3：某电话交换台每分钟接到的呼叫数X，服从参数为5的泊松分布，求在一分钟内呼叫数X不超过6次的概率。

解：

指数分布E

注意：
$$\begin{gathered} PX已经怎样后，还能继续怎样=PX还能怎样 \\ 即P已经A，还想B=PB \end{gathered}$$

做个例题来练习一下套公式：
例1：
某种电子元件的使用寿命X (单位:小时)服从$$\lambda =\frac{1}{2000}$$的指数分布。求一个元件的正常使用时间在1000小时以下的概率。

解：

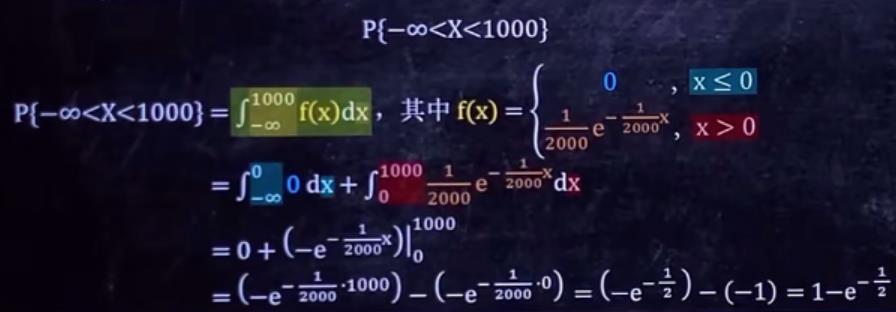
几何分布Ge

例1：
设随机变量$$X\sim Ge(\frac{1}{5})$$求PX=2,EX、DX。

解：
$$\begin{gathered} PX=2=\frac{4}{25} \\ EX=5 \\ DX=20 \end{gathered}$$