n个元素中有m个相同的元素,则这n个元素的全排列的种数是

Posted 2023-04-03

参考技术A 先排不相同的这（n－m）个,理解为：
在n个位置选择（n－m）个位置,再进行排列.
所以有：nC(n-m)*(n-m)!
余下的位置全排这m个相同的元素,不需要考虑.

算法习题---字符串的全排序列

一：什么是全排列

排列：从n个元素中任取m个元素，并按照一定的顺序进行排列，称为排列；

全排列：当n==m时，称为全排列；

比如：集合{ 1,2,3}的全排列为：

{ 1 2 3}

{ 1 3 2 }

{ 2 1 3 }

{ 2 3 1 }

{ 3 2 1 }

{ 3 1 2 }

我们可以将这个排列问题画成图形表示，即排列枚举树，比如下图为{1,2,3}的排列枚举树，此树和我们这里介绍的算法完全一致；

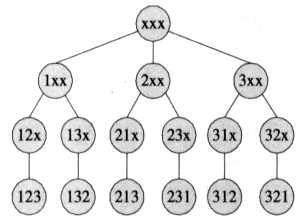
二：全排列实现思路

(1)n个元素的全排列=（n-1个元素的全排列）+（另一个元素作为前缀）；

(2)出口：如果只有一个元素的全排列，则说明已经排完，则输出数组；

(3)不断将每个元素放作第一个元素，然后将这个元素作为前缀，并将其余元素继续全排列，等到出口，出口出去后还需要还原数组；

三：代码实现

//str是字符串，n是由n个不同字符串组成，k是处理下标从0-k的所有字符串进行全排列
void perm(char str[], int k, int n)
{
    int i, j;
    char temp;
    if (k==0)    //输出排列完毕的字符串
    {
        for (j = 0; j <= n - 1; j++)
            printf("%d", str[j]);
    }
    else
    {
        for (i = 0; i <= k;i++)    //对每一个字符尝试一次做第一个排序字符
        {
            temp = str[k];    //交换，将每一个元素放在最后
            str[k] = str[i];
            str[i] = temp;

            perm(str, k - 1, n);

            temp = str[i];    //打印完毕，将数组还原
            str[i] = str[k];
            str[k] = temp;
        }
    }
}