概率论与数理统计猴博士 笔记 p38-40 切比雪夫不等式大数定律中心极限定理

Posted 2022-05-17 karshey

文章目录

• • 切比雪夫不等式
  • 大数定律
  • 中心极限定理

切比雪夫不等式

题干特征：

1. 求的P里面有不等式
2. 求的概率的事件是某个绝对值
3. 求的P里面的不等式符号与外面的不等式符号相反

满足以上特征就要用到切比雪夫不等式。

做法：
注意：公式求出来的是绝对值大于等于a的概率

下面练习一下套公式：
例1：

解：
直接套公式.
答案1/4

例2：

解：
E(X+Y)=EX+EY=0;
满足条件，可以直接套公式。
由上节课内容：已知相关系数和方差，可求协方差Cov(X,Y).
已知DX,DY,Cov(X,Y)，可求D(X+Y)——D(X+Y)=DX+DY+2Cov(X,Y).

答案为D(X+Y)/a²=1/12

例3：

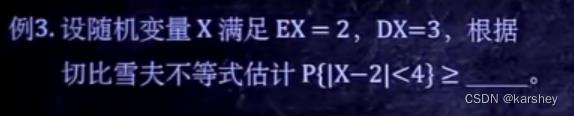
解：
套公式可知：
P|X-2|>=4=3/16
所以P|X-2|<4=1-3/16=13/16

大数定律

题干特征：

• 随机变量相互独立且都服从同一个分布
• 求n->∞时的P的极限/收敛

图中的四种描述方式其实表示同一个意思。

做法：

例题1：

解：

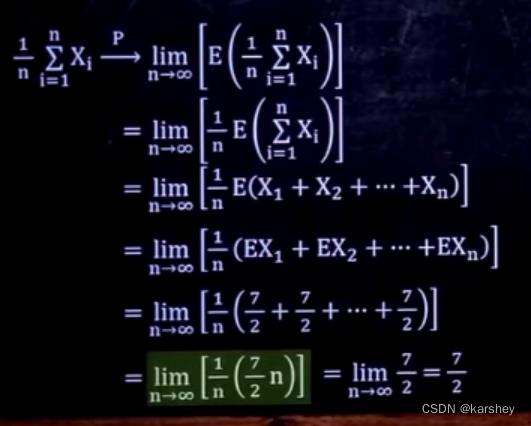
7/2的来源：

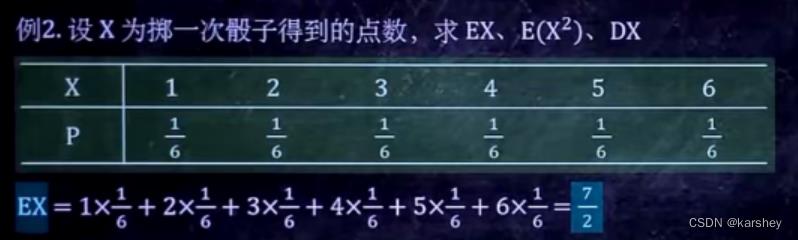
例题2：这里题目给错了，没有那个平方。

解：

EX=2的来源：

中心极限定理

题干特征：

• 变量独立同分布
• 求X和

做法：

例题1：

解：
指数分布：

套公式得C。

例题2：

解：
由题意得到EX和DX，根据中心极限定理可知Sn~N(nEX，nDX)。
将Sn标准化，得到的式子与题目给出的带有a、b的式子相似，通分一下可以得出a、b。

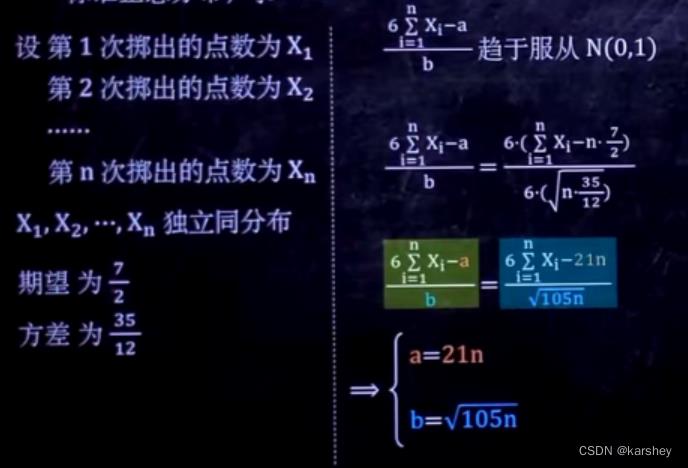
期望和方差的来源：

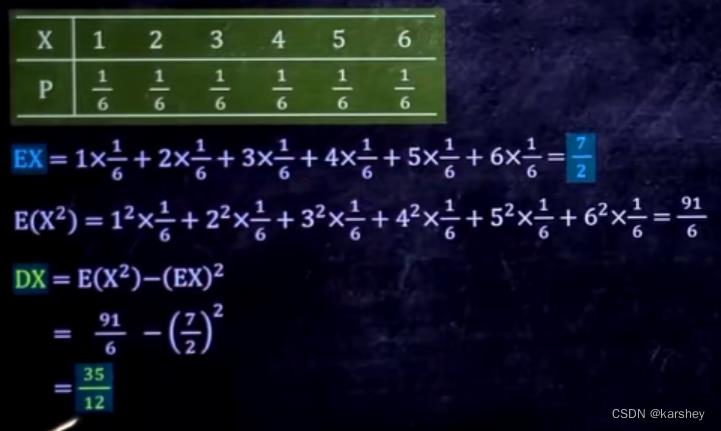
例3：

解：
最多可以装98箱。

P与fai 的转化：