概率论与数理统计猴博士 笔记 p15-16 一二维连续型求概率

Posted 2022-04-11 karshey

一维连续型求概率

题型如下：

解题步骤如下：
其实就是求积分

举例1的例子：

例2：

解：

例3：

解：
注意：要把Y变为X计算，且要分类讨论y是否大于0.

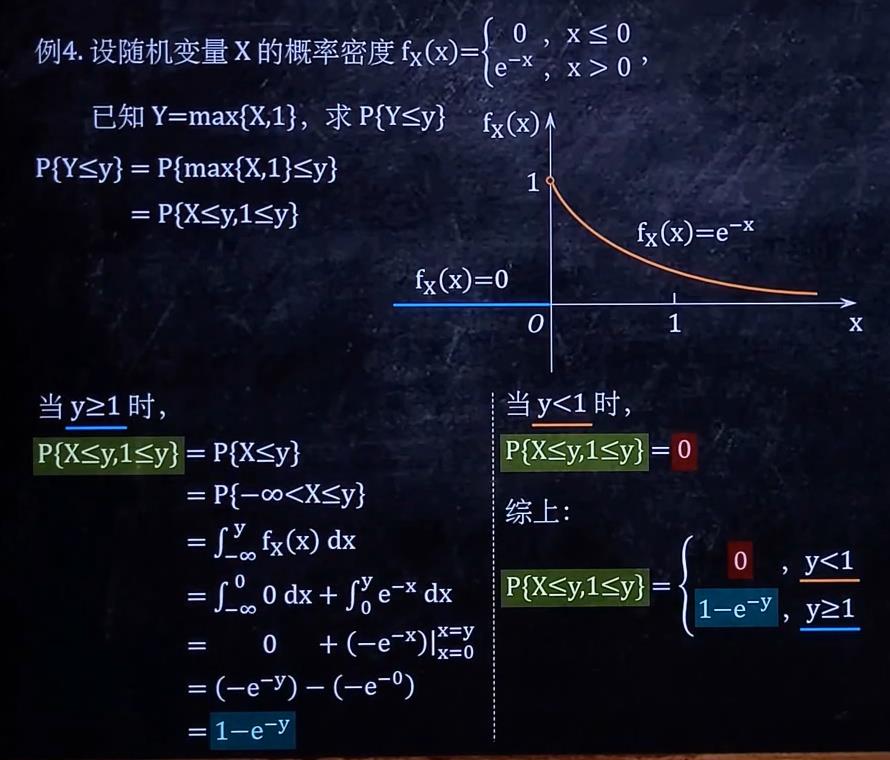
例4：

解：
去掉max和min的方法：

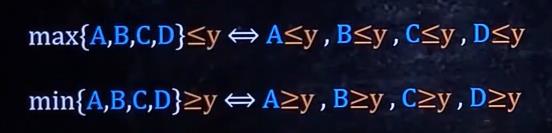
去掉多余项的方法：

假设要求AB两项同时发生的概率，当多余项（A）必然发生时，两个事件同时发生的概率其实就是B发生的概率。

具体解：

例5：（猴博士：大概是一维连续型求概率的最难的题型）

解：

$$\begin{gathered} 注意，对P2\le y,x\le 1来说，2\le y是一个确定的范围， \\ 所以它算是多余项，判断是否一定发生 \\ 但是Px\le y,x\le 1中x\le y不是一个确定的范围， \\ 所以要对y分类讨论 \end{gathered}$$
对答案合并的方法：

答案：

一些小知识点：
这三个是一个意思：

二维连续型求概率

题型如下：给出f(x,y)，求P

步骤：求二重积分

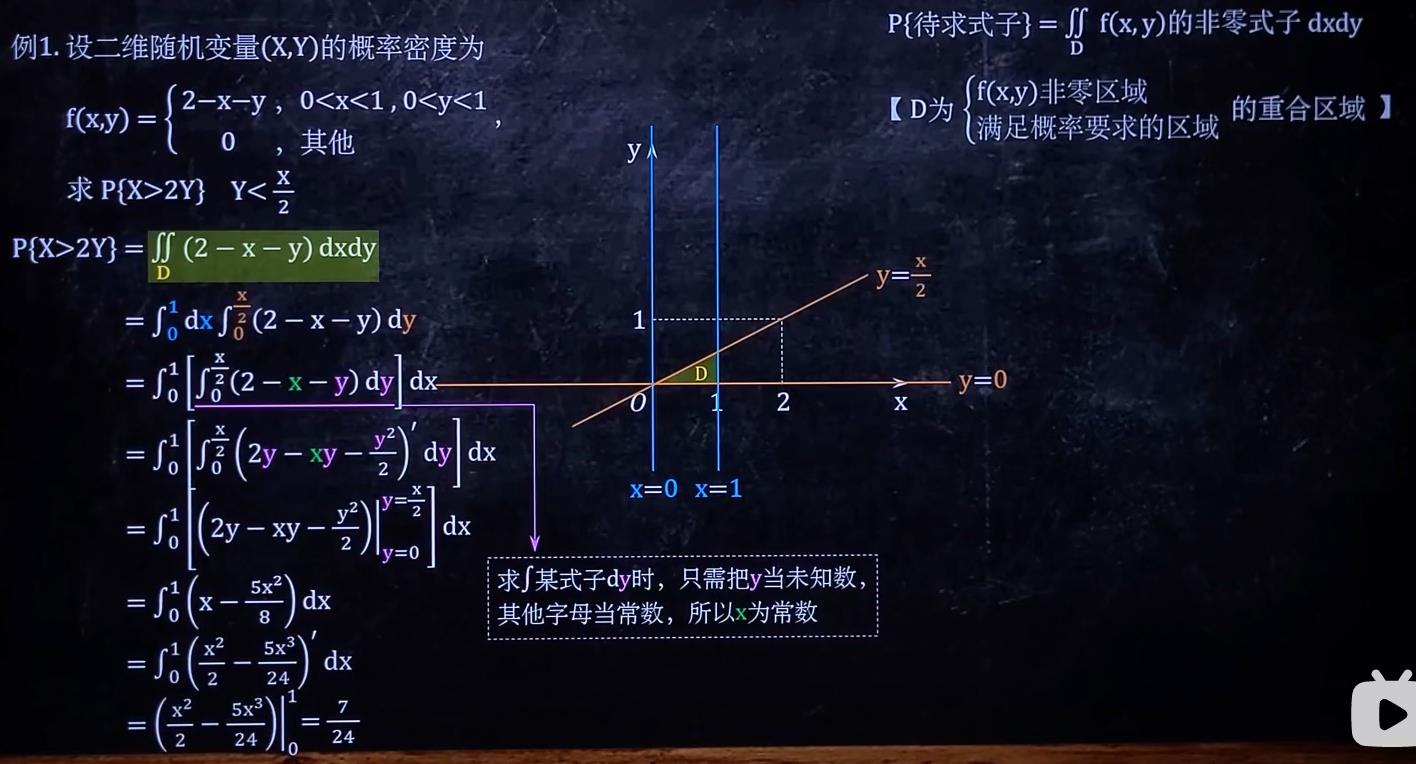
看例1题解：

$$注意，x的范围是(0,1),但y的范围是(0,\frac{x}{2}),而不是(0,\frac{1}{2})$$

例2：

这是一道要分析D的题目：
$$\begin{gathered} D为\begin{array}{l}f(x,y)非零区域\\ 满足概率要求的区域\end{array}的重合区域 \\ 我们先找f(x,y)非零区域，画出坐标系， \\ 把坐标系上每个点连线，且每个点都做平行于x和y的虚线 \\ 最左边线的左边和最下面线的下面都是其他情况 \\ 剩下的所有格子都要分类讨论 \end{gathered}$$
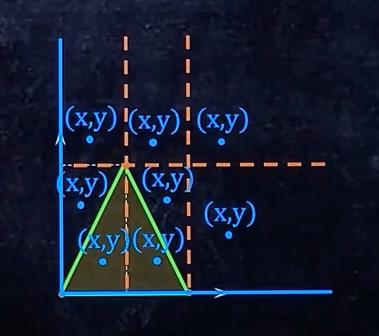
如：
这个坐标系的左线的左边和下线的下面都是其他情况。

再举个例子：荧光笔部分为其他情况。

然后剩下六个格子，其中两个格子中有概率范围，所以一共有八种情况需要讨论（六个不在概率里的格子，两个在概率里的格子）。

我们回到例2，因此例2要讨论四种情况+其他情况（其他情况下无重合区域）：

因此，积分的结果是个大括号：

然后计算，把结果填上去即可：

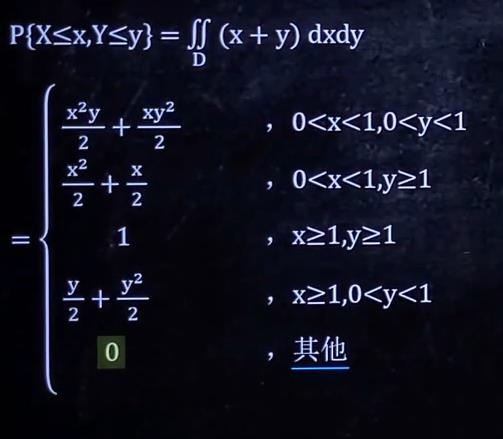
例3：

到这里就应该知道这道题该怎么做了：

$$\begin{gathered} 这里Z=X+2Y，可以给出Y关于X和Z的表达式 \\ 由于f(x,y)的非0区域为x>0,y>0 \\ 画出相交的图后发现只有Z>0的时候才存在重合区域 \\ 因此分为Z>0,Z\le 0两种情况分类讨论即可 \\ (只有前者有积分，后者为0) \end{gathered}$$

画出图：

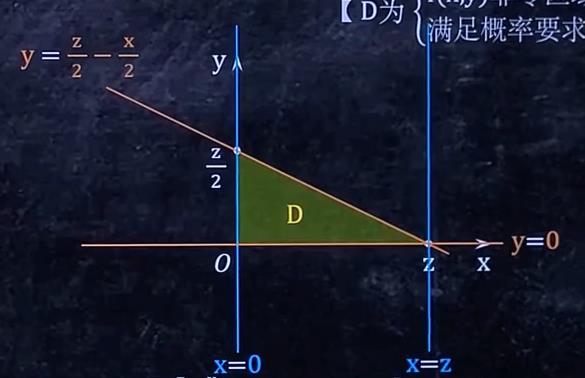
得知：
$$x的积分范围是(0,z),y的积分范围是(0,\frac{z}{2})$$
答案：

小补充：这三个其实求的是一样的