背景数学知识简述

Posted 2022-06-16 大饼博士X

文章目录

• 第2章 背景数学知识简述
• • 2.1 数学分析和微积分基础
  • • 函数性质
    • 集合Sets
    • Norms
    • 线性函数、仿射函数
    • 函数的微分（导数）
  • 2.2 线性代数基础
  • • Matrix Subspaces
    • 正定和半正定矩阵
    • 特征分解
    • 奇异值分解Singular Value Decomposition
    • 矩阵伪逆Pseudo-inverse
    • 舒尔补、分块矩阵求逆公式
  • 2.3 经典机器学习算法
• 参考资料

第2章 背景数学知识简述

主要参考是[1]和[2]的内容。特别是[2]，比较简明又全面的介绍了需要的数学背景知识。主要需要数学分析（主要是实分析，Real analysis）, 微积分（calculus）, 以及线性代数（linear algebra）的最基础数学背景知识。

2.1 数学分析和微积分基础

函数性质

• 极限：
  

• 连续：
  
  一个函数$f$在$x$点连续（dom表示定义域），说明一定存在一个点$y$，当和$x$足够近的时候，他们的函数值也一定足够近。

• 可微：
  
  一个函数$f$在点$x$上可微的定义如上，看起来比较复杂。其中$Df(x)$叫做函数在$x$的微分（也叫Jacobian矩阵，一元变量的时候一般叫导数，但是很多时候说导数其实就是说微分，混着用），记成：
  
  函数$f$在点$x$的一阶近似，称为affine function，形式如下。当$z$非常接近$x$的时候，affine function非常接近$f$.
  $$f(x)+Df(x)(z-x)$$

• 光滑： $f$ is smooth if the derivatives of $f$ are continuous over all of dom $f$

• Lipschitz连续：A function $f$ is Lipschitz with Lipschitz constant $L$ if
  $$\Vert f(x)-f(y)\Vert \le L\Vert x-y\Vert ,\forall x,y\in domf$$
  If we refer to a function f as Lipschitz, we are making a stronger statement about the continuity of f. A Lipschitz function is not only continuous, but it does not change value very rapidly, either.

• 泰勒展开Taylor Expansion：一个函数的一阶泰勒展开，是函数的线性近似
  $$f(y)\approx f(x)+▽f(x)(y-x)$$
  可以看成是函数$f(x+(y-x))$在$x$处展开。二阶泰勒展开形式是
  $$f(y)\approx f(x)+▽f(x)(y-x)+\frac{1}{2}(y-x{)}^T{▽}^{2}f(x)(y-x)$$

集合Sets

• Interior内点集：
  
  意思是说，以x为中心，存在一个球全部在集合C中，那么x就是集合C的一个内点。虽然上面是用欧氏距离来定义距离的，实际上所有的norm形式都可以同样的内点集合。所有集合C的内点集合叫做C的interior，记为 $\text{int}C$.

• 补集：The complement of the set $C\subseteq R^n$ is denoted by $R^n\setminus C$. It is the set of all points not in C.

• 开集：A set C is open if $\text{int}C=C$, i.e., every point in C is an interior point.

• 闭集：A set $C\subseteq R^n$ is closed if its complement $R^n\setminus C=x\in R^n|x\notin C$ is open.

• 闭包Closure：
  
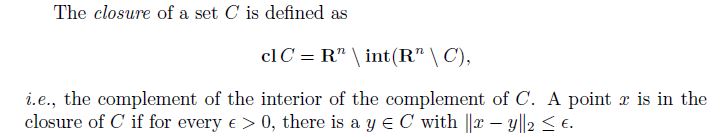
  理解有点复杂，后半句是说，如果$x$属于集合C的闭包中，那么就是说集合C中存在着和$x$点无限接近的点（$y$）。

• 边界：
  很形象，如果一个C上的点$x$，存在和它无限接近的点$y$在C中，也存在和它无限接近的点$z$不在集合C中，那么$x$就是一个边界点。边界的概念也可以用来区分开集和闭集——如果一个集合C包含了它的边界，那么是闭集；如果C和它的边界点集合的交集为空，那么它是开集。

Norms

• 内积、欧氏距离、项链夹角
  
• 常见的例子：$l_0,l_1,l_2,l_{\infty }$

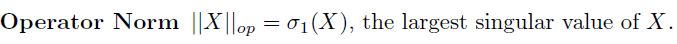
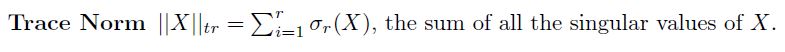
• Frobenius norm：
  
• Dual norm：这个概念在优化理论推导的时候貌似是很重要的，但是目前我还不能体会精华，就先放一下截图，不详细展开。以后如果能更理解透彻，再来补充。
  

线性函数、仿射函数

函数的微分（导数）

这一块在[2]中的附录讲的比较详细，这里不展开特别多的。

• 矩阵乘积和矩阵逆的微分
  
  

• 矩阵迹的微分（Derivative of Traces）
  在机器学习中，有时候需要对一个矩阵的F模进行微分，而矩阵的F是可以转换为矩阵的迹，矩阵的迹的微分的计算可以帮助我们计算矩阵的F模的微分。比如在线性回归模型中，输出不是0和1，而是一个向量，这时整个输出矩阵就不是向量而是矩阵的。这会在最后的例子中具体说明。[3]

• 矩阵的F模和迹的关系：
  
  其中$A^{\ast }$是$A$的共轭转置。矩阵的迹的性质
  

Matrix Cookbook中给出了矩阵迹的微分的一般表达式： $\frac{\partial }{\partial x}tr(F(x))=f(x{)}^T$。其中，$f()$是$F()$的微分。
给一下常用的求矩阵微分的公式：

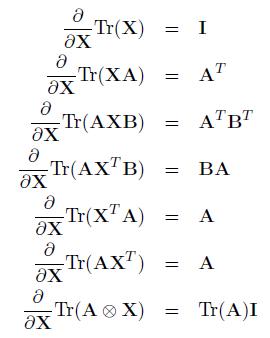
2.2 线性代数基础

Matrix Subspaces

• 矩阵值域Range： 矩阵$A\in R^{m\times n}$，A的值域Range的含义：$x$是一个任意的n维向量，经过矩阵A（m*n的矩阵）变换后，得到的所有可能的n维向量的集合就是A的值域。或者说，the set of all vectors in $R^m$ that can be written as linear combinations of the columns of A. 记成：

$$R(A)=Ax|x\in R^n$$

• 行空间Row Space: The row space of a matrix A is the subspace spanned of the rows of A.
• 列空间Column Space: The column space of a matrix A is the subspace spanned of the columns of A.
• 零空间Null Space: The null space of a matrix A is the set of all x such that $Ax=0$.
• 矩阵的秩Rank：线性无关的列数（或者行数），$rankA\le minm,n$，满秩的时候取等号。如果矩阵A是方阵并且满秩，那么A是可逆的。
• 正交子空间Orthogonal Subspaces：
  

正定和半正定矩阵

下面给出最最基本的矩阵特征分解以及SVD分解的形式，具体应用就需要大家自己再去理解了。

特征分解

一般写成下面这样的形式：

特征值全部非零 <==>那么矩阵A可逆，是等价的两个条件。而且很重要的是，可以直接对特征值逐个求逆就行了。特征值一般习惯用降序排列，也就是说${\lambda }_1$是最大特征值。这里的大小是用数值比较的，也就是正的大于负的，而不是看绝对值大小。

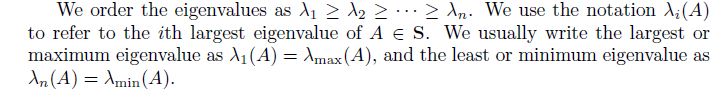
下面两种Norm的定义，可以用特征值来表示。F-norm稍微说下，很容易理解,用特征分解：
∣ ∣ A ∣ ∣ F 2 = t r a c e ( A T A ) = t