2021-11-16：最长递增子序列的个数。给定一个未排序的整数数组，找到最长递增子序列的个数。注意: 给定的数组长度不超过 2000 并且结果一定是32位有符号整数。力扣673。

Posted 2021-12-13 福大大架构师每日一题

2021-11-16：最长递增子序列的个数。给定一个未排序的整数数组，找到最长递增子序列的个数。注意: 给定的数组长度不超过 2000 并且结果一定是32位有符号整数。力扣673。

答案2021-11-16：

我的思路是：1.另外开辟一个等长度的数组lens存递增子序列长度和一个等长度的数组cnts存个数。2.遍历lens，找到最大值的序号。3.根据序号找cnts里的值并且求和，获取最大值的个数，这个值就是需要的返回值。
时间复杂度：O(N**2)。可优化成O(N*logN)。
额外空间复杂度：O(N)。

代码用golang编写。代码如下：

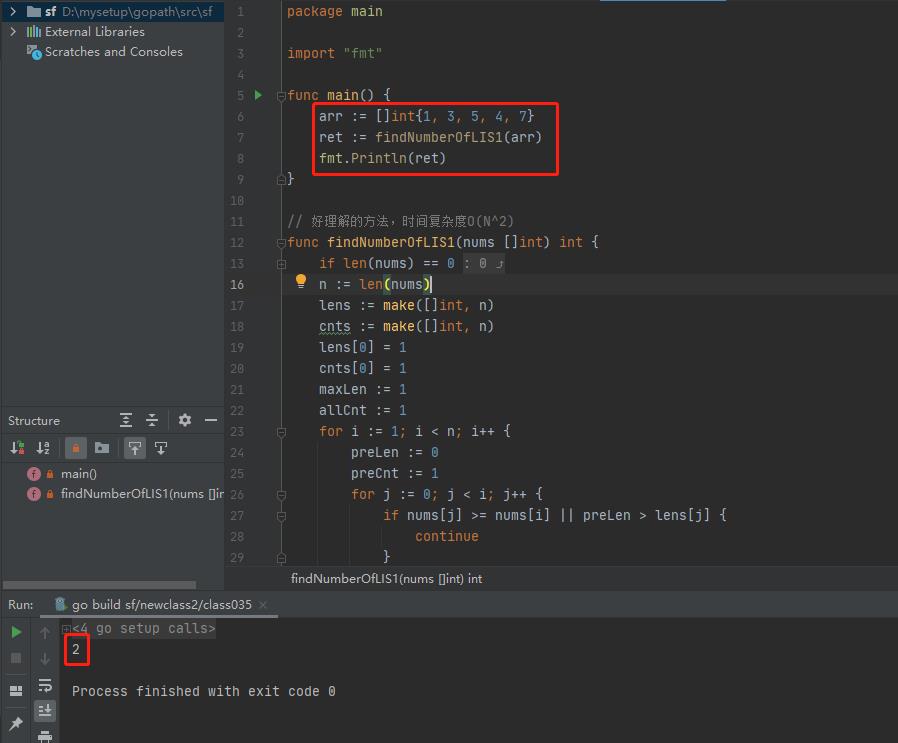
package main

import "fmt"

func main() {
    arr := []int{1, 3, 5, 4, 7}
    ret := findNumberOfLIS1(arr)
    fmt.Println(ret)
}

// 好理解的方法，时间复杂度O(N^2)
func findNumberOfLIS1(nums []int) int {
    if len(nums) == 0 {
        return 0
    }
    n := len(nums)
    lens := make([]int, n)
    cnts := make([]int, n)
    lens[0] = 1
    cnts[0] = 1
    maxLen := 1
    allCnt := 1
    for i := 1; i < n; i++ {
        preLen := 0
        preCnt := 1
        for j := 0; j < i; j++ {
            if nums[j] >= nums[i] || preLen > lens[j] {
                continue
            }
            if preLen < lens[j] {
                preLen = lens[j]
                preCnt = cnts[j]
            } else {
                preCnt += cnts[j]
            }
        }
        lens[i] = preLen + 1
        cnts[i] = preCnt
        if maxLen < lens[i] {
            maxLen = lens[i]
            allCnt = cnts[i]
        } else if maxLen == lens[i] {
            allCnt += cnts[i]
        }
    }
    return allCnt
}

执行结果如下：

---

左神java代码