673. 最长递增子序列的个数

Posted 2021-10-10 我要出家当道士

目录

1、Question 

 2、Analysis

 3、Code

 4、Execution

---

1、Question 

给定一个未排序的整数数组，找到最长递增子序列的个数。

示例 1:

输入: [1,3,5,4,7]
输出: 2
解释: 有两个最长递增子序列，分别是 [1, 3, 4, 7] 和[1, 3, 5, 7]。
示例 2:

输入: [2,2,2,2,2]
输出: 5
解释: 最长递增子序列的长度是1，并且存在5个子序列的长度为1，因此输出5。
注意: 给定的数组长度不超过 2000 并且结果一定是32位有符号整数。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/number-of-longest-increasing-subsequence
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

 2、Analysis

        很久没有做算法题了，没找到感觉，解体思路参考了官方的题解。

        主要是下面的公式： 

        

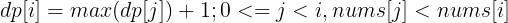
        dp[i] 记录了 nums[0:i] 中最长递增子序列长度。

        这题的的难点不仅仅是求出最长递增子序列的长度，还需要求出个数。

         定义一个cnt数组变量，用于记录 nums[0:i] 中满足最长递增子序列长度的子序列个数。cnt[i] 等于所有满足 dp[j] + 1 == dp[i] 的 cnt 之和。道理很简单，假设最长递增子序列长度为 maxLen，所有长度满足 maxLen 的子序列都是在长度为 maxLen - 1的子序列基础上添加第 i 位得到的，所以长度满足 maxLen 的子序列数量就是所有长度满足 maxLen - 1 的子序列数量之和；

        具体题解请阅读：点我！点我！点我

 3、Code

int findNumberOfLIS(int* nums, int numsSize)
{
	//记录nums数组中最大递增子序列长度以及个数
	int maxLen = -1, maxCnt = -1; 
    int *dp = (int *)malloc(sizeof(int) * numsSize);
    int *cnt = (int *)malloc(sizeof(int) * numsSize);
    // 分别计算nums[0:i]对应的dp[i]和cnt[i] 
	for(int i = 0; i < numsSize; i++)
	{
		// init dp[i] and cnt[i]
		dp[i] = 1;
		cnt[i] = 1;
		// search max(j)
		for (int j = 0; j < i; j++)
		{
			if (nums[i] > nums[j])
			{
				if (dp[j] + 1 > dp[i])
				{
					dp[i] = dp[j] + 1;
					// reset cnt[i].
					cnt[i] = cnt[j];
				}
				else if (dp[j] + 1 == dp[i])
					cnt[i] += cnt[j];
					
			}	
		} 
		if (dp[i] > maxLen)
		{
			maxLen = dp[i];
			maxCnt = cnt[i];
		}
		else if (dp[i] == maxLen)
			maxCnt += cnt[i];
	}
	return maxCnt;
}

 4、Execution