现代控制理论基础四控制系统的稳定性

Posted 2021-09-10 AXYZdong

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了现代控制理论基础四控制系统的稳定性相关的知识，希望对你有一定的参考价值。

Author：AXYZdong 自动化专业工科男
有一点思考，有一点想法，有一点理性！
定个小小目标，努力成为习惯！在最美的年华遇见更好的自己！
CSDN@AXYZdong，CSDN首发，AXYZdong原创
唯一博客更新的地址为： 👉 AXYZdong的博客 👈
B站主页为：AXYZdong的个人主页

文章目录

4.1 李雅普诺夫关于稳定性的定义

设所研究系统的齐次状态方程为：
$\\acute{x}=f(x,t) \\tag 1$
式中， $x$ 为 $n$ 维状态矢量； $f$ 为与 $x$ 同维的矢量函数，它是 $x$ 各元素 $x_1,x_2,\\cdots,x_n$ 和时间 $t$ 的函数。

设方程式（1）在给定初始条件 $t_0,x_0)$ 下，有唯一解： $x=\\phi(t;x_0,t_0) \\tag 2$

式（2）实际上描述了系统式（1）在 $n$ 维状态空间中从初始条件 $t_0,x_0)$ 出发的一条状态运动的轨迹，简称系统的运动或 状态轨迹。

若式（1）存在状态矢量 $x_e$ ，对所有 $t$ ，都使
$f(x_e,t)\\equiv0$
成立，则 $x_e$ 称为系统的平衡状态。

李雅普诺夫意义下稳定
如果方程式（1）描述的系统对于任意选定的实数 $\\epsilon >0$ ，都对应存在另一实数 $\\delta ( \\epsilon , t_0) >0$ ，使当 $||x_0-x_e||\\leq\\delta(\\epsilon,t_0)$
时，从任意初态 $x_0$ 出发的解都满足:
$||\\phi(t;x_0,t_0)-x_e||\\leq\\epsilon,t_0\\leq t< \\infty$
则称平衡状态 $x_e$ 为李雅普诺夫意义下稳定。其中实数 $\\delta$ 与 $\\epsilon$ 有关，一般情况下也与 $t_0$ 有关。如果 $\\delta$ 与 $t_0$ 无关，则称这种平衡状态是一致稳定的。

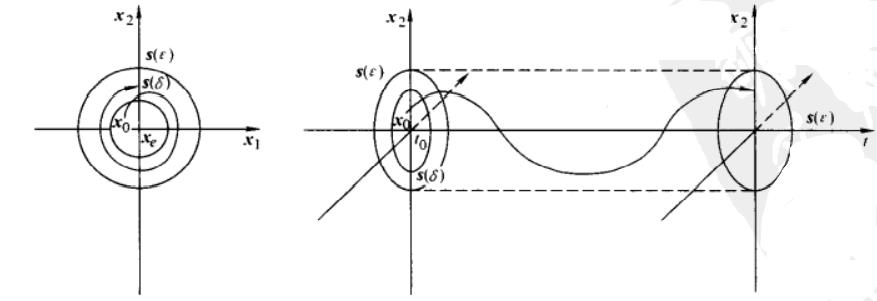
^{▲ 稳定的平衡状态及其状态轨线}

渐进稳定
如果平衡状态 $x_e$ 是稳定的，而且当 $t$ 无限增长时，轨线不仅不超出 $s(\\epsilon)$ ，而且最终收敛于 $x_e$ ，则称这种平衡状态 $x_e$ 渐近稳定。

^{▲ 渐进稳定的平衡状态及其状态轨线}

大范围渐进稳定
如果平衡状态 $x_e$ 是稳定的，而且从状态空间中所有初始状态出发的轨线都具有渐近稳定性，则称这种平衡状态 $x_e$ 大范围渐进稳定。
不稳定
如果对于某个实数 $\\epsilon>0$ 和任一实数 $δ ＞ 0$ ，不管 $\\delta$ 这个实数多么小，由 $s(\\delta)$ 内出发的状态轨线，至少有一个轨线越过 $s(\\epsilon)$ ，则称这种平衡状态 $x_e$ 不稳定。

^{▲不稳定的平衡状态及其状态轨线}

如果 $x (t)$ 有界，则称 $x_e$ 稳定。如果 $x (t)$ 不仅有界而 $\\lim_{t\\to \\infty} x(t) = 0$ ，收敛于原点，则称 $x_e$ 渐近稳定。如桌 $x (t)$ 为无界，则称 $x_e$ 不稳定。
在经典控制理论中，只有渐进稳定的系统才称作稳定系统。只在李雅普诺夫意义下稳定，但不是渐近稳定的系统则称临界稳定系统，这在工程上属于不稳定系统。

4.2 李雅普诺夫第一法（间接法）

（状态稳定性）线性定常系统 $\\sum:(A,b,c)$
$\\acute{x}=Ax+bu\\\\ y=cx$
平衡状态 $x_e$ 渐进稳定的充要条件是矩阵 $A$ 的所有特征值均具有负实部。
（输出稳定性）线性定常系统 $\\sum:(A,b,c)$ 输出稳定的充要条件是其传递函数：
$W(s)=c(sI-A)^{-1}b$
的极点全部位于 $s$ 的左半平面。

4.3 李雅普诺夫第二法

定理：
设系统状态方程为 $\\acute{x}=f(x)$