现代控制理论基础三控制系统的能控性和能观测性
Posted AXYZdong
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了现代控制理论基础三控制系统的能控性和能观测性相关的知识,希望对你有一定的参考价值。
Author:AXYZdong 自动化专业 工科男
有一点思考,有一点想法,有一点理性!
定个小小目标,努力成为习惯!在最美的年华遇见更好的自己!
CSDN@AXYZdong,CSDN首发,AXYZdong原创
唯一博客更新的地址为: 👉 AXYZdong的博客 👈
B站主页为:AXYZdong的个人主页
文章目录
3.1 能控性及其判据
指外输入 u ( t ) u(t) u(t) 对系统状态变量 x ( t ) x(t) x(t) 和输出变量 y ( t ) y(t) y(t) 的支配能力,它回答了 u ( t ) u(t) u(t) 能否使 x ( t ) x(t) x(t) 和 y ( t ) y(t) y(t) 做任意转移的问题。
- 有些状态分量能受输入 u ( t ) u(t) u(t) 的控制,有些则可能不受 u ( t ) u(t) u(t) 的控制。受 u ( t ) u(t) u(t) 控制的状态称为能控状态,不受 u ( t ) u(t) u(t) 控制的状态称为不能控状态。
3.1.1 例子
例1:系统的结构图如下
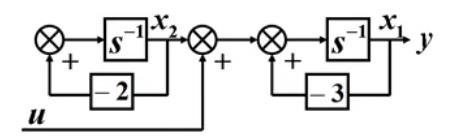
显然,
u
u
u 只能控制
x
1
x_1
x1 ,而不能影响
x
2
x_2
x2 ,我们称状态变量
x
1
x_1
x1 是可控的,而
x
2
x_2
x2 是不可控的。
- 只要系统中有一个状态变量是不可控的,则该系统是状态不可控的。
例2:取 i L i_L iL 和 u c u_c uc 作为状态变量, u u u 为输入, y = u c y=u_c y=uc 为输出。
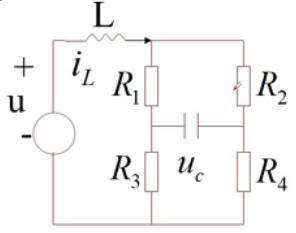
- 当 R 1 R 4 ≠ R 2 R 3 R_1R_4\\neq R_2R_3 R1R4=R2R3,状态可控;
- 当 R 1 R 4 = R 2 R 3 R_1R_4= R_2R_3 R1R4=R2R3 , u u u 只能控制 i L i_L iL,状态不可控。
3.1.2 能控性定义
对于线性定常系统:
x
ˊ
=
A
x
+
B
u
其
中
,
x
、
u
分
别
为
n
、
r
维
向
量
A
为
n
×
n
常
值
矩
阵
,
B
为
n
×
r
常
值
矩
阵
(1)
\\acute{x}=Ax+Bu \\tag 1 \\\\[2ex]其中,x、u分别为n、r维向量\\\\[2ex]A为n\\times n常值矩阵,B为n\\times r常值矩阵
xˊ=Ax+Bu其中,x、u分别为n、r维向量A为n×n常值矩阵,B为n×r常值矩阵(1)
如果存在一个分段连续系统的输入
u
(
t
)
u(t)
u(t),能在
[
t
0
,
t
f
]
[t_0,t_f]
[t0,tf] 的有限时间内使得系统的某一初始状态
x
(
t
0
)
x(t_0)
x(t0) 转移到任一终端状态
x
(
t
f
)
x(t_f)
x(tf),则称此状态是能控的。
如果系统的所有状态都是能控的,则称系统是状态完全能控的。
根据初始状态和终端状态的不同位置,可以分为:
- 系统的状态能控性:(常用)
初始状态为状态空间任意非零有限点;
终端状态为状态空间原点,即零态。 - 系的状态能达性:
初始状态为为状态空间原点,即零态;
终端状态为状态空间任意非零有限点。
3.1.2 能控性判据
- 格拉姆矩阵法
对于式(1)的系统状态能控的充分必要条件是矩阵 W c [ 0 , t 1 ] W_c[0,t_1] Wc[0,t1] 的秩为 n n n ,其中
W c [ 0 , t 1 ] = ∫ 0 t 1 e − A τ B B T e − A T τ d τ W_c[0,t_1]=\\int_{0}^{t_1}e^{-A\\tau}BB^Te^{-A^T\\tau}d\\tau Wc[0,t1]=∫0t1e−AτBBTe−ATτdτ
- 若式(1)系统能控,则
n
×
n
r
n\\times nr
n×nr 能控性矩阵
Q c = ( B A B A 2 B ⋯ A n − 1 B ) Q_c= \\begin{pmatrix} B & AB &A^2B&\\cdots &A^{n-1}B \\end{pmatrix} Qc=(BABA2B⋯An−1B)
满秩。即:
r a n k Q c = n rankQ_c=n rankQc=n
- PHB判别法
式(1)的系统能控的充分必要条件是 n × ( n + r ) 矩 阵 [ λ I − A ∣ B ] n\\times (n+r)矩阵[\\lambda I-A|B] n×(n+r)矩阵[λI−A∣B] 对 A A A 的所有特征值 λ i \\lambda_i λi之秩都是 n n n。即:
r a n k [ λ i I − A ∣ B ] = n , ( i = 1 , 2 , . . . , n ) rank[\\lambda_i I-A|B]=n ,(i=1,2,...,n) rank[λiI−A∣B]=n,(i=1,2,...,n)
- 式(1)系统的矩阵 A A A 特征值 λ i ( i = 1 , 2 , . . . , n ) \\lambda_i(i=1,2,...,n) λi(i=以上是关于现代控制理论基础三控制系统的能控性和能观测性的主要内容,如果未能解决你的问题,请参考以下文章