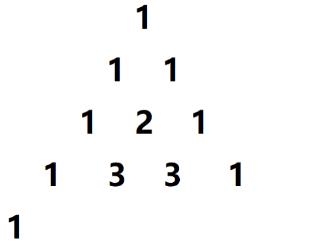⭐算法入门⭐《递推 - 二维》简单01 —— LeetCode 118. 杨辉三角

Posted 2021-08-16 英雄哪里出来

🙉饭不食，水不饮，题必须刷🙉
还不会C语言，和我一起打卡！ 🌞《光天化日学C语言》🌞
LeetCode 太难？上简单题！ 🧡《C语言入门100例》🧡
LeetCode 太简单？大神盘他！ 🌌《夜深人静写算法》🌌

文章目录

• 一、题目
• • 1、题目描述
  • 2、基础框架
  • 3、原题链接
• 二、解题报告
• • 1、思路分析
  • 2、时间复杂度
  • 3、代码详解
• 三、本题小知识

一、题目

1、题目描述

  给定一个非负整数 $numRows$，生成杨辉三角的前 $numRows$ 行。
在杨辉三角中，每个数是它 左上方 和 右上方 的数的和。
  样例输入： 5
  样例输出：

2、基础框架

• c++ 版本给出的基础框架代码如下：

class Solution {
public:
    vector<vector<int>> generate(int numRows) {
    }
};

• 可以理解成返回的是一个二维数组。
  

3、原题链接

LeetCode 118. 杨辉三角

二、解题报告

1、思路分析

• 根据杨辉三角的定义，我们可以简单将上面的图进行一个变形，得到：

于是，我们可以得出以下结论：
  1）杨辉三角的所有数可以存储在一个二维数组中，行代表第一维，列代表第二维度；
  2）第 $i$ 行的元素个数为 $i$ 个；
  3）第 $i$ 行 第 $j$ 列的元素满足公式：$$c[i][j]=\{\begin{array}{ll}1& i=0\\ c[i-1][j-1]+c[i-1][j]& otherwise\end{array}$$

• 于是就可以两层循环枚举了。

2、时间复杂度

• 两层循环嵌套，所以时间复杂度 $O(n^2)$。

3、代码详解

class Solution {
public:
    vector<vector<int>> generate(int numRows) {
        vector<vector<int>> ans;
        for(int i = 0; i < numRows; ++i) {                        // (1)
            vector<int> v;
            for(int j = 0; j <= i; ++j) {                         // (2)
                if(j == 0 || j == i) {
                    v.push_back(1);                               // (3)
                }else { 
                    v.push_back( ans[i-1][j-1] + ans[i-1][j] );   // (4)
                }
            }
            ans.push_back(v);
        }
        return ans;
    }
};

• $(1)$ 第一层循环枚举行；
• $(2)$ 第二层循环枚举列，列的上限为行编号；
• $(3)$ 杨辉三角两边恒为 1；
• $(4)$ 杨辉三角中间的数，为 c[i-1][j-1] + c[i-1][j]；

---

三、本题小知识

学会了组合数的递推求解。

---