⭐算法入门⭐《坐标转换》中等01 —— LeetCode 74. 搜索二维矩阵

Posted 2021-08-16 英雄哪里出来

🙉饭不食，水不饮，题必须刷🙉
还不会C语言，和我一起打卡！ 🌞《光天化日学C语言》🌞
LeetCode 太难？上简单题！ 🧡《C语言入门100例》🧡
LeetCode 太简单？大神盘他！ 🌌《夜深人静写算法》🌌

文章目录

• 一、题目
• • 1、题目描述
  • 2、基础框架
  • 3、原题链接
• 二、解题报告
• • 1、思路分析
  • 2、时间复杂度
  • 3、代码详解
• 三、本题小知识

一、题目

1、题目描述

  编写一个高效的算法来判断 $m\times n$ 矩阵中，是否存在一个目标值。该矩阵具有如下特性：
   1）每行中的整数从左到右按升序排列。
   2）每行的第一个整数大于前一行的最后一个整数。
  样例输入： $matrix=[[1,2,3,4],[5,6,8,9],[16,19,27,99]],target=3$
  样例输出： true

2、基础框架

• c++ 版本给出的基础框架代码如下：

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
    }
};

• 输入数组参数类型是vector<vector<int>>&，代表的是一个引用类型的二维数组，按照题目要求，需要返回一个这个二维数组中是否存在 $target$ 这个值；
  

3、原题链接

LeetCode 74. 搜索二维矩阵

二、解题报告

1、思路分析

• 首先，我们来看个图：
  
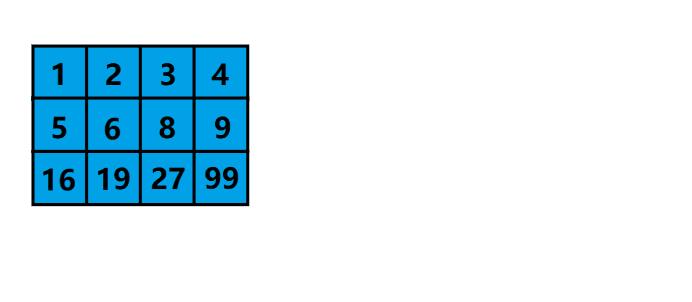
• 对于这个特殊的二维数组，我们可以将它转换成一个有序的一维数组，然后就可以在一维数组上做二分查找了。
• 对于一个 $n\times m$ 的矩阵，我们可以从左往右，从上往下进行编号，令一维编号为 $i$，二维编号的行为 $r$，列为 $c$，于是就有 $r$ 和 $c$ 关于 $i$ 的表达式如下：
• $$\begin{gathered} r=\lfloor \frac{i}{m}\rfloor \\ c=imodm \end{gathered}$$
• 于是只要二分枚举 $i$，就能对应找到矩阵里的值，然后和目标值进行大小判定，从而调整迭代 $i$ 的值，就像一维的二分枚举一样。

2、时间复杂度

• 查找的时间复杂度为 $O(lo{g}_{2}n+lo{g}_{2}m)$。

3、代码详解

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int n = matrix.size();                       // (1)
        int m = matrix[0].size();                    // (2)
        int l = 0, r = n * m - 1;                    // (3)
        while(l <= r) {
            int mid = (l + r) >> 1;                  // (4)
            int row = mid / m;                       // (5)
            int col = mid % m;
            if(matrix[row][col] == target) {
                return true;
            }else if(target > matrix[row][col]) {
                l = mid + 1;
            }else {
                r = mid - 1;
            }
        }
        return false;
    }
};

• $(1)$ 获取矩阵的行 $n$；
• $(2)$ 获取矩阵的列 $m$；
• $(3)$ 定义一维数组下标的范围是 $[0,nm)$；
• $(4)$ 二分枚举的是一维数组的下标；
• $(5)$ 将一维数组的下标转换成二维数组的下标，然后去二维数组进行索引获得值进行二分判定；
• 关于二分查找的内容，可以参考这个题：《二分枚举》简单01 —— LeetCode 704. 二分查找。

---

三、本题小知识

可以用 除法 和 取模 来实现两个分量的坐标转换。

---