算法入门01二维数组中的查找

Posted 2021-09-22 2021dragon

核心考点：数组相关，特性观察，时间复杂度把握

在一个二维数组中（每个一维数组的长度相同），每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样一个二维数组和一个整数，判断数组中是否含有该整数。

解析一：（不提倡）
这种在二维数组当中进行查找的问题，很多人的思路就是依次遍历二维数组当中的元素进行查找。

class Solution {
public:
	bool Find(int target, vector<vector<int> > array) {
		for (int i = 0; i < array.size(); i++)
		{
			for (int j = 0; j < array[i].size(); j++)
			{
				if (target == array[i][j])
					return true; //找到了返回true
			}
		}
		return false; //没找到返回false
	}
};

解析二：（正解）
查找的过程本质上是排除的过程，若逐个遍历二维数组进行查找，那么我们一次只能排除一个元素，我们应该充分利用题目所给条件进行查找。

对此，我们可以让待查找数字先与第一行最后一个元素进行比较（或是先于第一列最后一个元素比较，比较逻辑变一下即可）。
若待查找数字比该元素大，则我们就无需再在第一行进行查找了，因为第一行的元素中最后一个元素最大，待查找元素比这个元素都大了，那必定比该行其他元素也大。

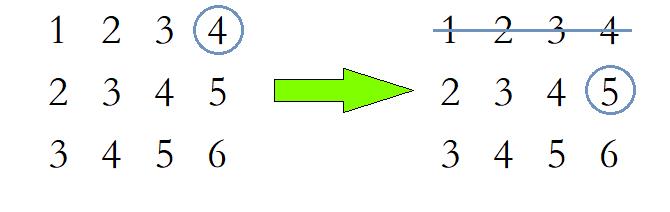
若待查找数字比该元素小，则我们就无需再在最后一列进行查找了，因为最后一列的元素中第一行的元素最小，待查找元素比这个元素还要小，那必定比该列其他元素也小。

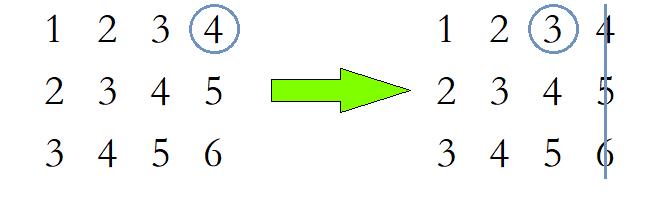
这样一来，经过一次判断我们就可以排除一行或是一列元素，相比一次排除一个元素来说，那真是快了太多了。而经过一次判断后，剩下的仍然是一个二维数组，我们可以通过相同的方法对其再次进行判断，直到找到这个元素或是将整个二维数组遍历结束。

class Solution {
public:
	bool Find(int target, vector<vector<int> > array) {
		int i = 0, j = array[0].size() - 1;
		while (i < array.size() && j >= 0)
		{
			if (target > array[i][j]) //待查找数字比该元素大
			{
				i++; //无需在改行进行查找了
			}
			else if (target < array[i][j]) //待查找数字比该元素小
			{
				j--; //无需在该列进行查找了
			}
			else
			{
				return true; //找到了返回true
			}
		}
		return false; //数组遍历结束，未找到返回false
	}
};