信号与系统 2022 春季学期第一次作业

Posted 2022-03-01 卓晴

 

◎ 本文下载连接

• 信号与系统 2022 春季学期第一次作业 : https://zhuoqing.blog.csdn.net/article/details/123113465

 

§01 作业内容

---

  作业包含有六道大题。请注意，每道题目中包含有必做题和选做题。必做题要求包含在提交的作业中；选做题仅用于思考和练习。

1.1 绘制信号波形

1.1.1 题目要求

  请根据下面信号的函数表达式，绘制出信号的波形。请注意：

• 函数变量为 $t$ 的信号为 连续时间信号； ;
• 函数变量为 $n$ 的信号为 离散时间信号 ;

  绘制波形可以手工绘制，也可以通过MATLAB ，Python以及其他编程绘图语言绘制。

1.1.2 题目内容

（1）必做题

 Ⅰ.带有直流分量正弦振荡信号

 Ⅱ.幅度调制正弦振荡信号

 Ⅲ.双边指数衰减振荡信号

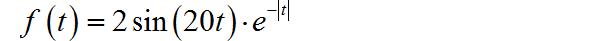
 Ⅳ.复合信号

 Ⅴ.有限长指数信号

 Ⅵ.指数序列信号

 Ⅶ.左边指数序列信号

提示：请注意这是一个左边指数序列信号。

（2）选做题

 Ⅰ.sinc函数连续乘积信号

  其中： $\sin c\left(t\right)=\sin \left(t\right)/t$ 。

关于为什么研究多个sinc函数相乘，大家可以参见博文： 数学中的虚幻模式 。这是一个复杂的波形，建议使用计算机辅助绘制该函数波形。

 Ⅱ.振荡序列信号

注意：序列函数中的自变量是 $n$ 的平方。请观察序列，并判断该序列是否为周期序列信号？

 Ⅲ.非周期振荡信号

这个函数具有无穷多个极大值，极小值。在博文 傅里叶变换中的狄利克雷条件 分析了它的傅里叶变换的特点。

 Ⅳ.波形发散的周期信号

提示：这个周期信号将来会在傅里叶变换的狄利克雷条件中分析。在博文 傅里叶变换中的狄利克雷条件 分析了它的傅里叶变换的特点。也请大家思考一下，这个函数在单个周期内：

• 面积是否有限？
• 能量是否有限？

1.2 写出信号函数表达式

1.2.1 题目要求

  根据下面信号的波形，写出对应的函数表达式。注意，同样一个波形可能会存在多种等效的函数表达式。

1.2.2 题目内容

（1）必做题

 Ⅰ.对称三角波信号

▲ 图1.2.1 对称三角波信号

 Ⅱ.分段跃变直流信号

▲ 图1.2.2 分段直流跃变信号

 Ⅲ.升余弦脉冲信号

▲ 图1.2.3 升余弦脉冲信号

我不能直接给你写出升余弦脉冲信号表达式，否则就不用你来完成这个题目里。所谓升余弦脉冲信号，就是把余弦振荡信号叠加一个直流信号，使得它整体网上平移，最低点为 0。然后再截取其中 一个周期内的波形作为脉冲信号的波形。

 Ⅳ.单边正弦信号

▲ 图1.2.4 单边正弦信号

注意：在 $t<0$ 时，对应的 $f\left(t\right)=0$ 。信号波形往右无线延拓。

 Ⅴ.单边衰减振荡信号

▲ 图1.2.5 单边指数衰减振荡信号

（2）选做题

 Ⅰ.周期方波信号

▲ 图1.2.6 周期方波信号

提示：参考前面绘制信号波形中的“复合函数”，以及应用 $u\left(t\right)$ 的特点。

 Ⅱ.阶跃衰减信号

  下面是一个阶跃衰减信号，它：

• 只在 $\left(0,1\right)$ 之间取值；
• 起始值 $f\left(0\right)=1$ ，终值 $f\left(t\right)=0,t\ge 1$ ；
• 从0到1过程中，每前进剩余距离一半幅值就降低一半。

▲ 图1.2.7 阶跃衰减信号

这个函数将会在第三章，在分析傅里叶变换的狄利克雷条件时被被提到。在。在博文 傅里叶变换中的狄利克雷条件 分析了它的傅里叶变换的特点。

1.3 判断信号的周期性

1.3.1 题目要求

  判断下列各信号是否为周期信号？如果是周期信号求出其基本周期。

1.3.2 题目内容

（1）必做题

 Ⅰ.正弦信号叠加

 Ⅱ.复指数调制信号

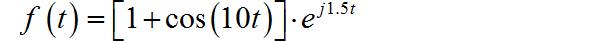
 Ⅲ.方波信号

 Ⅳ.正弦信号的三次方

 Ⅴ.自变量三次方的正弦振荡信号

 Ⅵ.自变量的三次方正弦序列信号

请对比离散时间信号与前面连续时间信号的异同

（2）选做题

 Ⅰ.线性信号与振荡信号叠加

 Ⅱ.判断题

  已知两个序列之间满足 $y\left[n\right]=x\left[2n\right]$ 。请问：

• 如果 $y\left[n\right]$ 是周期信号，那么 $x\left[n\right]$ 是否也是周期信号？
• 如果 $x\left[n\right]$ 是周期信号，那么 $y\left[n\right]$ 是否 也是周期信号？

1.4 冲激信号的抽样特性

1.4.1 题目要求

  根据冲激信号 $\delta \left(t\right)$ 、冲激偶信号 ${\delta }^{\prime }\left(t\right)$ 的 抽样特性 ，求下面各个定积分的积分值。

  由于在课堂上先介绍了冲激信号的基本概念：

$$\delta \left(t\right)=\frac{d}{dt}u\left(t\right),{\delta }^{\prime }\left(t\right)=\frac{d}{dt}\delta \left(t\right)$$

  对于它们的抽样特性还没有展开讲解。这一部分请大家对课件【1.1.3.3.2】中关于单位冲激信号的三种定义（函数演变定义、Dirac定义、分配函数定义）进行阅读，基于此理解：

• 单位冲激信号的抽样特性；
• 单位冲激信号的偶对称性；
• 单位冲激信号的尺度特性；

  这些特性可以参考在课件【1.1.3.3.3】中总结的性质一览表：

▲ 图1.4.1 冲激信号与冲激偶信号特性表格

1.4.2 题目内容

（1）必做题

 Ⅰ.第一小题

提示：请注意积分里面的 $\delta \left(t/2\right)$ ，这需要应用到冲激信号的尺度特性。

 Ⅱ.第二小题

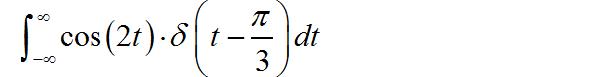
 Ⅲ.第三小题

注意：请分别讨论 $t_0$ 分别在大于0和小于0两者情况下的积分结果。

 Ⅳ.第四小题

（2）选做题

 Ⅰ.第五小题

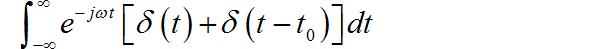
 Ⅱ.第六小题

1.5 信号的直流分量

  注意：本题都是选做题

1.5.1 题目要求

  分别求出下面周期信号的直流分量。

提示：周期信号的直流分量是它的一个周期的积分（面积）值除以周期。

1.5.2 题目内容

（1）选做题

 Ⅰ.第一小题

  全波整流信号：

 Ⅱ.第二小题

 Ⅲ.第三小题

 Ⅳ.第四小题

 

§02 实验内容

---

  下面两个实验题目都是选做题目，可以任选其中一个进行实验，来认知关于信号表达方式与信息传递之间的关系，并对MATLAB，PYTHON中用于信号处理的软件包进行初步的了解。

2.1 DTMF音频中的电话号码

  本题的背景来自于 技术宅的逆袭 - 牛逼大学生破译360总裁周鸿祎手机号 中介绍的一段有趣的新闻内容。详细内容大家可以参阅上面的网文。

  获得信号的时频联合分布，可以让我们了解音频信号中频率成分随着时间变化的信息。

2.1.1 题目要求

  从下面链接下载一段手机拨码音频，利用 MATLAB 中，或者PYTHON 中的 spectrogram 函数获得该音频信号的 时频联合分布图像，根据其中每个音频信号对应的频路组合，识别电话音乐中对应的电话号码。

• 电话音频文件下载链接 : https://gitee.com/tsinghuajoking/teaching-resources/raw/master/Signals&Systems/2022年/PhoneSound.wav

  下面给出了 DTMF编码方案 中每个电话号码对应的高频和低频频率组合。

▲ 图2.1.1 DTFM信号及其电话编码规格

2.1.2 编程处理示例

（1）MATLAB 示例

  下面给出了在MATLAB中处理DTMF 命令示例。

>> [s fs] = audioread('e:\\'bbflash\\'2.wav');
>> spectrogram(s(:,1), 2048, 1024, 1:2000, fs, 'yaxis');
>> plot((0:length(s)-1)/fs, s);

1.在MATLAB中使用audioread,audiowrite命令完成音频文件 的读取和存储。
2.在MATLAB中处理声音信号实际上是对连续声音信号的离散 采用数据进行处理。
3.对于音频信号的尺度变化，也可以试着改变音频文件的采 样率fs来达到同样的效果。

（2）PYTHON示例

  利用Python来显示信号的 Spectrogram 可以参照下面博文中给出的示例：

• 检测DTMF信号质量

2.2 饭盒弹拨乐器琴弦频率

  本文对一段由饭盒拨弦乐器所演奏的 女儿情 音乐，分析其中各个拨弦对应的频率，评价该一谈起中琴弦音准质量。

2.2.1 题目要求

  从下面链接下载 拨弦音乐的数据文件。通过 FFT（快速傅里叶变换，这部分内容将会在第三章进行讲解）来求取音频中每个琴弦频率分布。

▲ 图2.2.1 饭盒音乐中的琴弦频率

• 饭盒音乐音频文件下载链接 : https://gitee.com/tsinghuajoking/teaching-resources/raw/master/Signals&Systems/2022年/wave.mp3

2.2.2 参考处理方案

  具体处理方法可以参考博文： 女儿情：对于一段音乐进行频率频谱分析 给出的方案。

▲ 图2.2.2 演奏音乐过程

---

■ 相关文献链接:

• 连续时间信号；
• 离散时间信号
• 数学中的虚幻模式
• 傅里叶变换中的狄利克雷条件
• 抽样特性
• 技术宅的逆袭 - 牛逼大学生破译360总裁周鸿祎手机号
• 电话音频文件下载链接
• DTMF的原理：为什么选择这些频率？
• MT8870DTMF解码器测试
• 检测DTMF信号质量
• 女儿情
• 饭盒音乐音频文件下载链接
• 女儿情：对于一段音乐进行频率频谱分析

● 相关图表链接:

• 图1.2.1 对称三角波信号
• 图1.2.2 分段直流跃变信号
• 图1.2.3 升余弦脉冲信号
• 图1.2.4 单边正弦信号
• 图1.2.5 单边指数衰减振荡信号
• 图1.2.6 周期方波信号
• 图1.2.7 阶跃衰减信号
• 图1.4.1 冲激信号与冲激偶信号特性表格
• 图2.1.1 DTFM信号及其电话编码规格
• 图2.2.1 饭盒音乐中的琴弦频率
• 图2.2.2 演奏音乐过程