信号与系统分析2022春季作业-参考答案：第四次作业-第一部分

Posted 2022-04-21 卓晴

  封面动图来自于： SHUTTERSTOCK网站

 

§00 作业题目

---

  作业要求链接： 信号与系统2022春季学期第四次作业

 

§01 参考答案

---

1.1 求解卷积运算

1.1.1 求解两个信号卷积

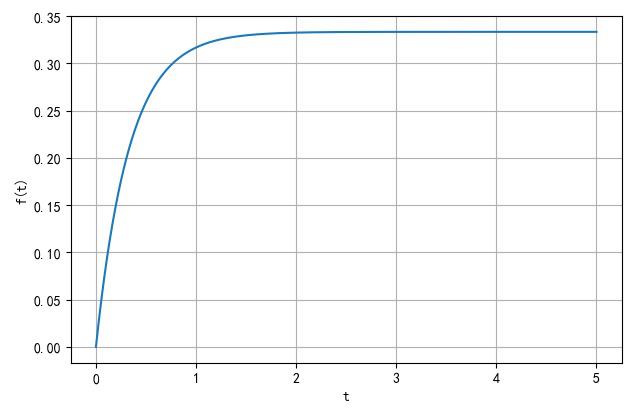
 Ⅰ.第一小题

  求解： 根据$u\left(t\right)$卷积特性：$u\left(t\right)\ast f\left(t\right)={\int }_{-\infty }^{t}f\left(\tau \right)d\tau$。所以：

$$f\left(t\right)=u\left(t\right)\ast e^{-3t}\cdot u\left(t\right)={\int }_0^t{e}^{-3\tau }d\tau ={\frac{-1}{3}{e}^{-3t}|}_0^t=\frac{1}{3}\left(1-e^{-3t}\right)$$

信号的波形：

^{▲ 信号f(t)的波形}

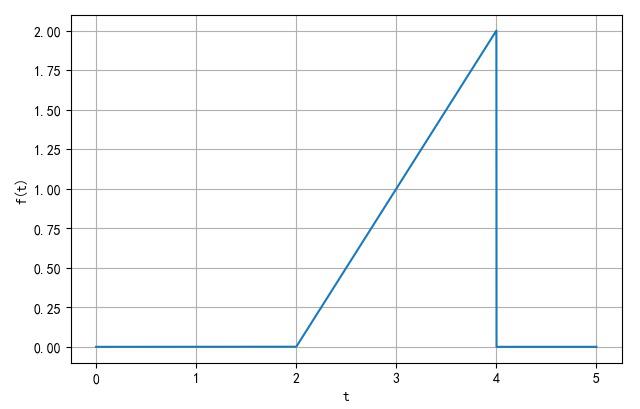
 Ⅱ.第四小题

  求解： 根据$\delta \left(t\right)$以下两个性质：

• 偶对称： $\delta \left(t\right)=\delta \left(-t\right)$
• 卷积特性：$f\left(t\right)\ast \delta \left(t-t_0\right)=f\left(t-t_0\right)$

  可以进行如下化简：

$$f\left(t\right)=t\left[u\left(t\right)-u\left(t-2\right)\right]\ast \delta \left(2-t\right)$$$$=t\left[u\left(t\right)-u\left(t-2\right)\right]\ast \delta \left(t-2\right)$$$$=\left(t-2\right)\cdot \left[u\left(t-2\right)-u\left(t-4\right)\right]$$

信号的波形：

^{▲ 信号f(t)的波形}

---

 Ⅲ.第七小题

  求解： 原来信号可以看成两个信号的卷积：$f\left(t\right)=f_1\left(t\right)\ast f_2\left(t\right)$：

• $f_1\left(t\right)=\left[\left(t+2\right)u\left(t+2\right)-2t\cdot u\left(t\right)+\left(t-2\right)\cdot u\left(t-2\right)\right]$
• $f_2\left(t\right)=\left[{\delta }^{\prime }\left(t+2\right)-{\delta }^{\prime }\left(t-2\right)\right]$

$f_1\left(t\right)$可以分解成两端组成：
$$f_1\left(t\right)=\left(t+2\right)\cdot u\left(t+2\right)-\left[\left(t+2\right)+\left(t-2\right)\right]\cdot u\left(t\right)+\left(t-2\right)\cdot u\left(t-2\right)$$$$=\left(t+2\right)\cdot [u\left(t+2\right)-u\left(t\right)信号与系统2022春季学期第四次作业$$

2021年春季学期-信号与系统-第十四次作业参考答案

信号与系统分析2022春季作业-参考答案：第五次作业

信号与系统分析2022春季作业-参考答案：第十次作业

信号与系统分析2022春季作业-参考答案：第三次作业-第二部分

信号与系统分析2022春季作业-参考答案：第十一次作业