信号与系统 2023(春季) 作业参考答案 - 第一次作业
Posted 卓晴
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了信号与系统 2023(春季) 作业参考答案 - 第一次作业相关的知识,希望对你有一定的参考价值。

01 基础练习
一、绘制信号波形
在下面给出的参考答案中, 使用了Python中的绘图工具,完成函数表达式的信号波形绘制。
1、必做题
(1) 单边指数信号

◎ 解答:
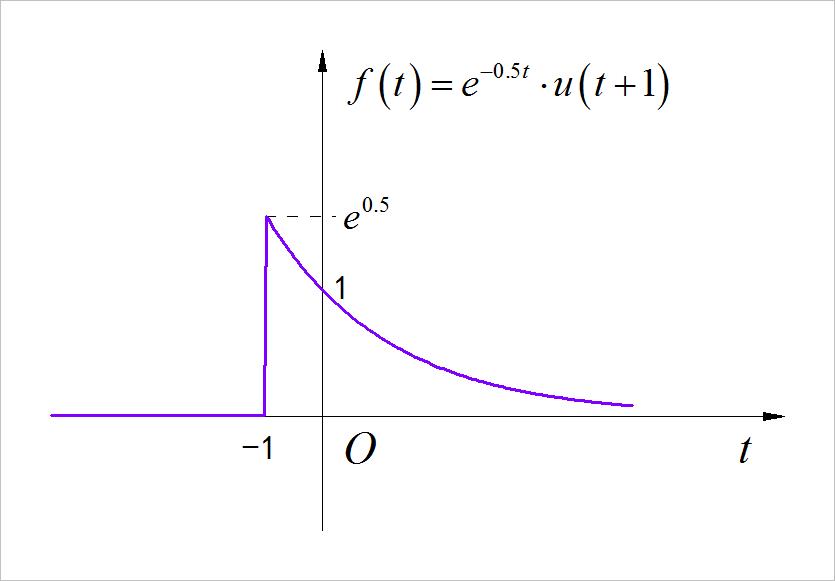
▲ 图1.1.1 信号波形

▲ 图1.1.2 信号波形
from headm import *
def f(x):
return exp(-0.5*x)*heaviside(x+1, 0.5)
t = linspace(-5, 5, 250)
ft = f(t)
plt.plot(t, ft, linewidth=3)
plt.xlabel("t")
plt.ylabel("f(t)")
plt.grid(True)
plt.title("exp(-0.5t)u(t+1)")
plt.tight_layout()
plt.show()
(2) 升余弦信号
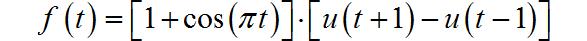
◎ 解答:

▲ 图1.1.3 信号波形
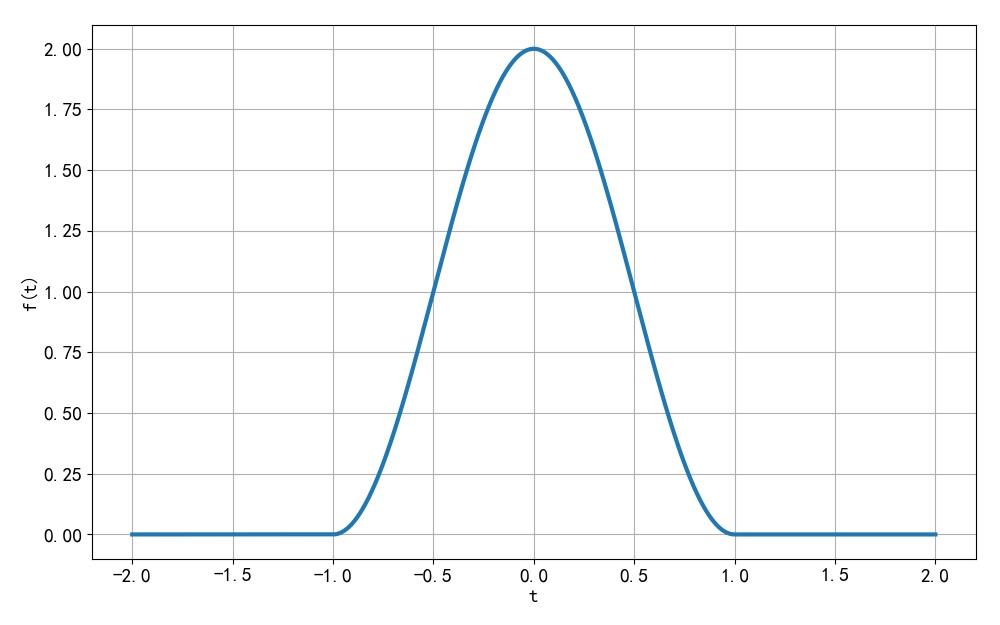
▲ 图1.1.4 信号波形
def f(t):
return (1+cos(pi*t))*(heaviside(t+1, 0.5)-heaviside(t-1, 0.5))
t = linspace(-2, 2, 250)
ft = f(t)
(3) 正弦调制的高斯信号
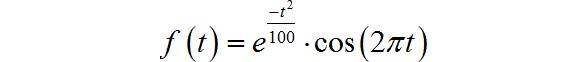
◎ 解答:

▲ 图1.1.5 信号波形
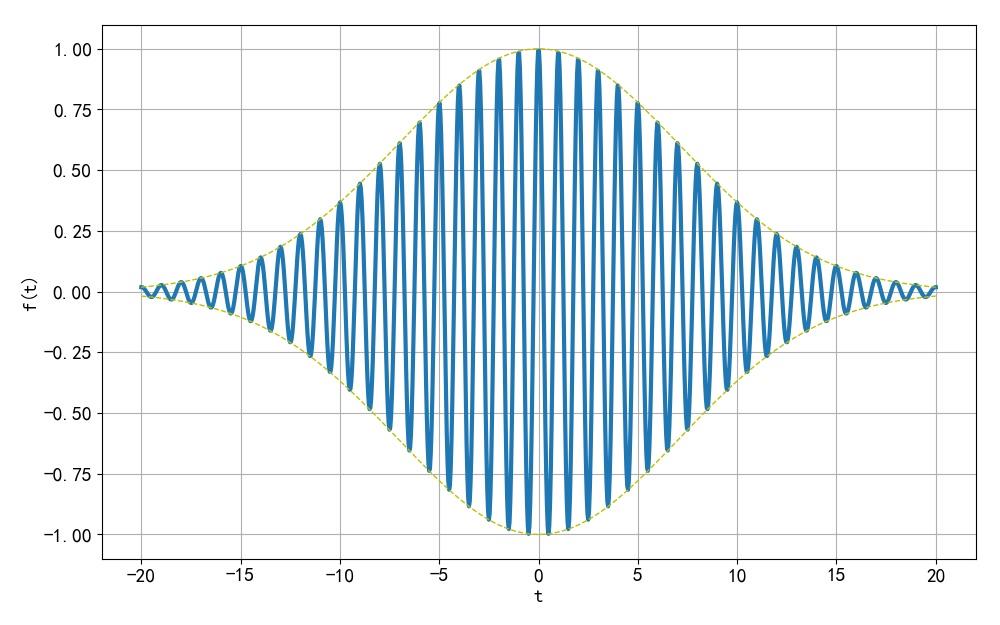
▲ 图1.1.6 信号波形
from headm import *
def f(t):
return exp(-t**2/100)*cos(2*pi*t)
t = linspace(-20, 20, 1000)
ft = f(t)
envelope_up = exp(-t**2/100)
envelope_down = -exp(-t**2/100)
clipboard.copy(str(ft))
plt.plot(t, ft, linewidth=3)
plt.plot(t, envelope_up, 'k--', linewidth=1)
plt.plot(t, envelope_down, 'k--', linewidth=1)
plt.xlabel("t")
plt.ylabel("f(t)")
plt.grid(True)
plt.title("exp(-0.5t)u(t+1)")
plt.tight_layout()
plt.show()
(4)复合信号
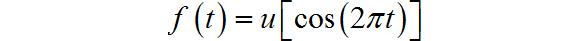
◎ 解答:
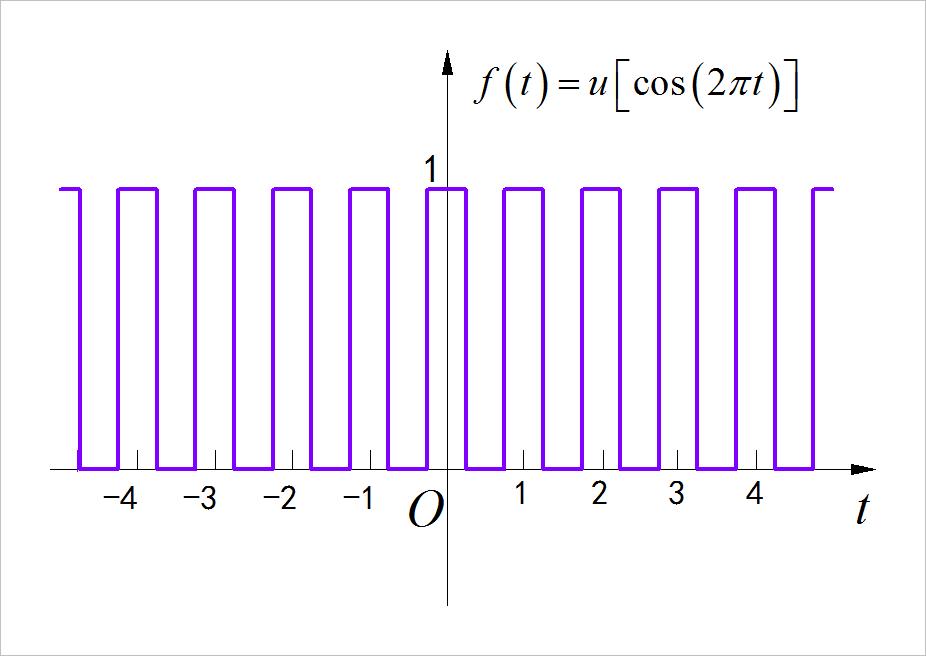
▲ 图1.1.7 信号波形
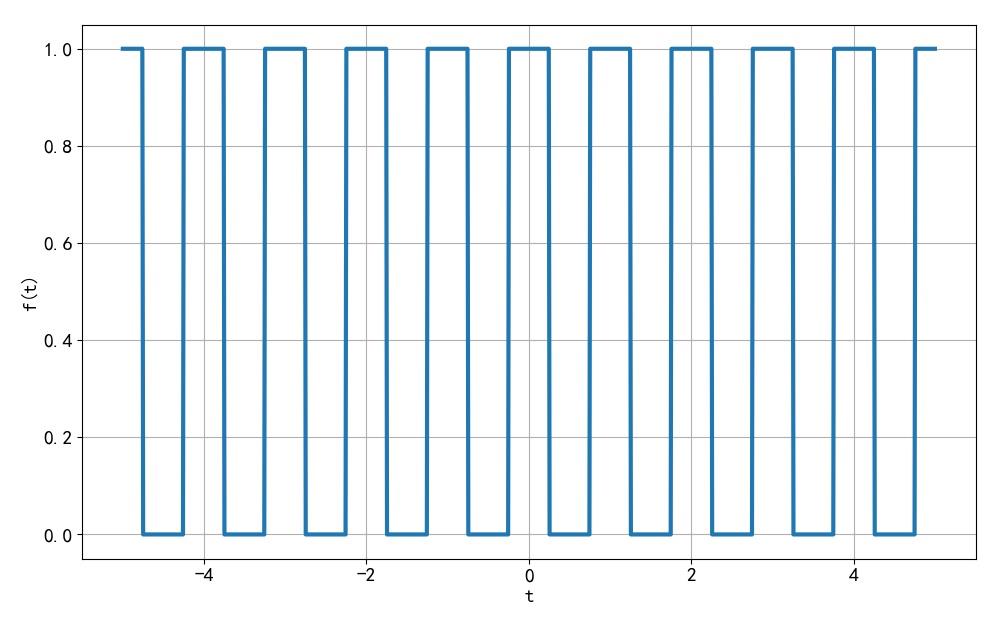
▲ 图1.1.8 信号波形
(5)衰减振荡序列
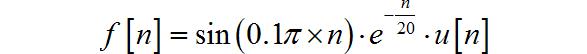
◎ 解答:
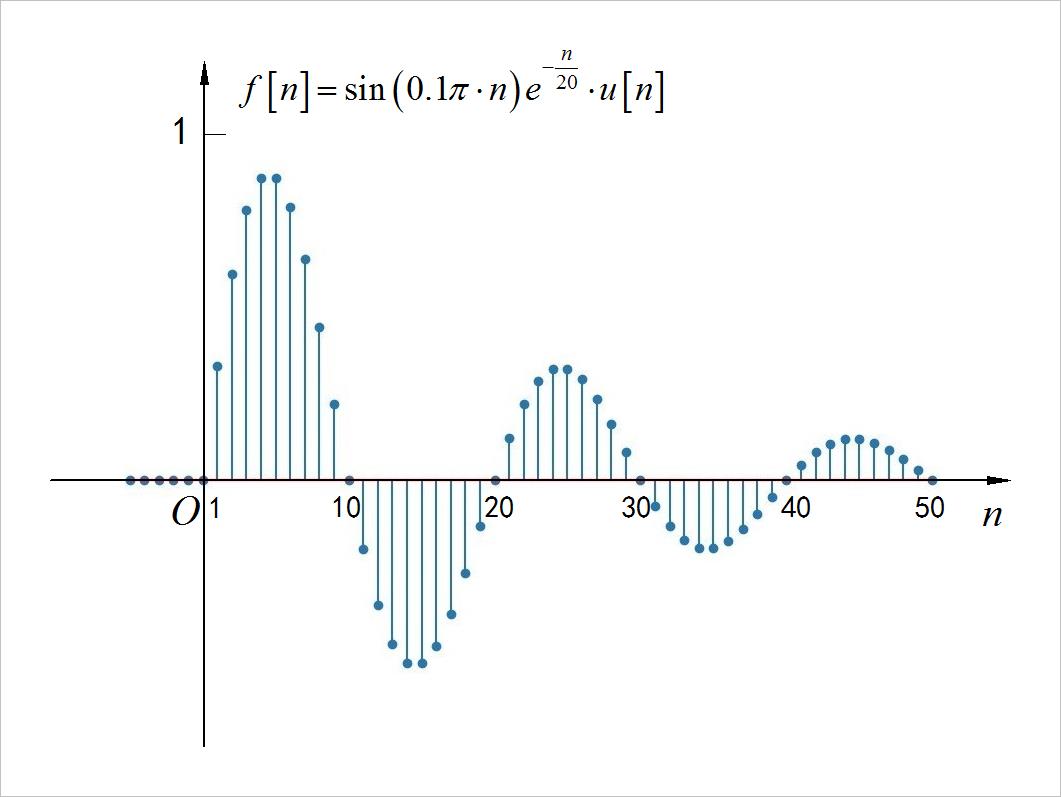
▲ 图A1.1.9 信号波形
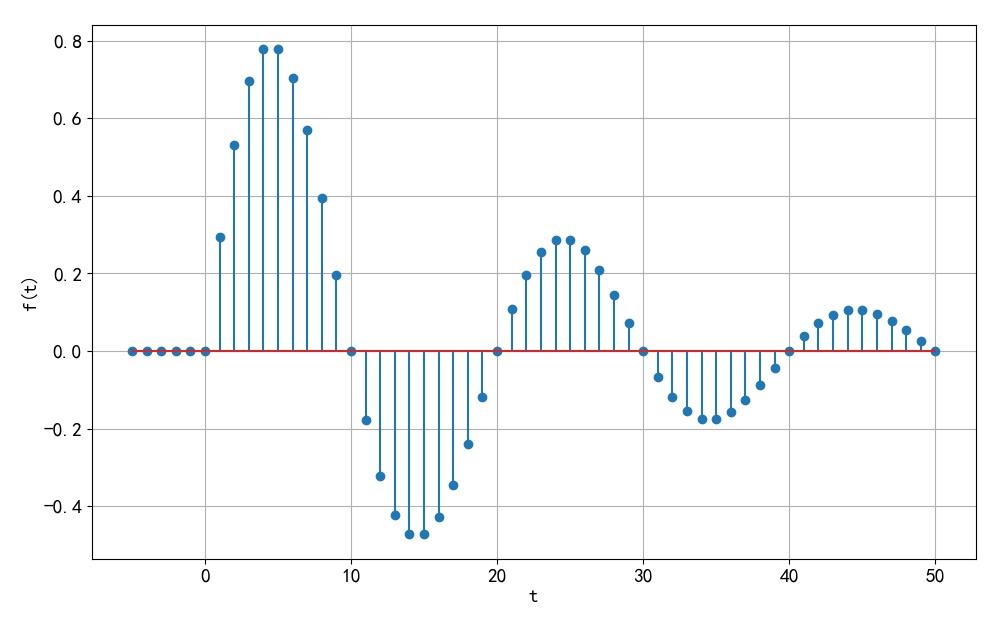
▲ 图1.1.9 信号波形
from headm import *1
def f(t):
return sin(0.1*pi*t)*exp(-t/20)*heaviside(t, 0.5)
startn = -5
endn = 50
t = linspace(startn, endn, endn-startn+1, endpoint=True)
ft = f(t)
clipboard.copy(str(ft))
plt.stem(t, ft)
plt.xlabel("t")
plt.ylabel("f(t)")
plt.grid(True)
plt.tight_layout()
plt.show()
(6)双边sinc函数序列
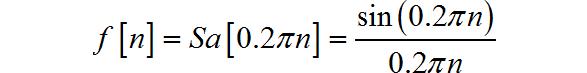
◎ 解答:

▲ 图A1.1.11 信号波形
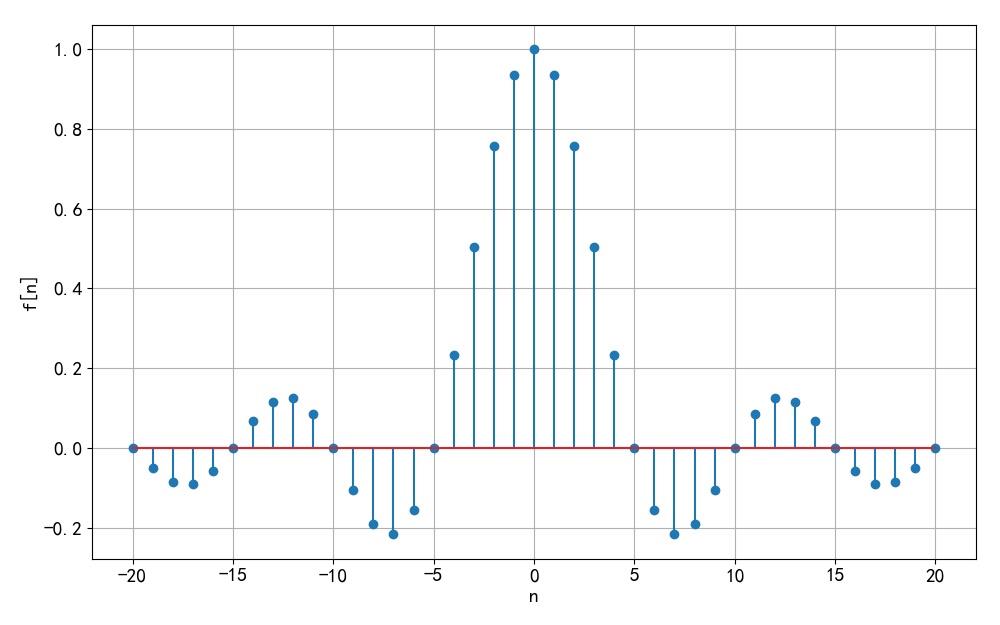
▲ 图1.1.12 信号波形
(7)窗口序列
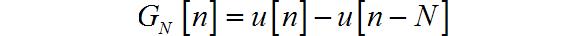
其中: N = 8 N = 8 N=8
◎ 解答:

▲ 图1.1.13 信号波形

▲ 图1.1.14 信号波形
2、选做题
(1) 电容放电信号波形
在下面阻容放电回路中, 电容C1、电阻R1的标称值在电路中已经标明。 在时间 t = 0 t = 0 t=0 时,电容的初始电压为 1V。 请绘制出在 t ≥ 0 t \\ge 0 t≥0 之后,电阻 R1 上的电压 U O ( t ) U_O \\left( t \\right) UO(t) 的信号波形。
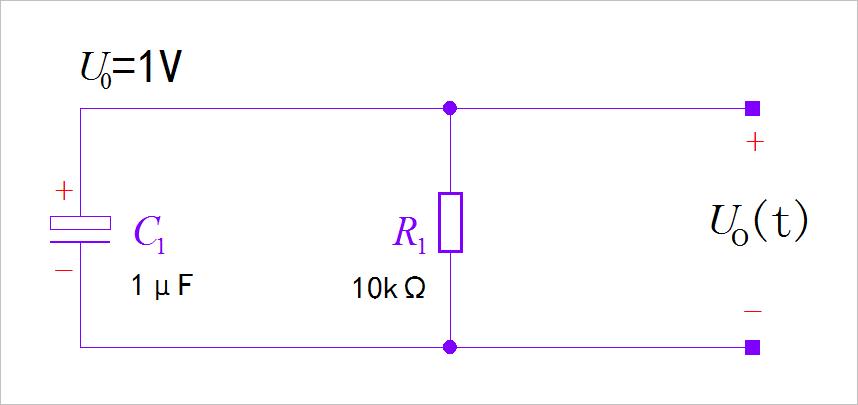
▲ 图A2.1.1 电容放电电路
◎ 解答:
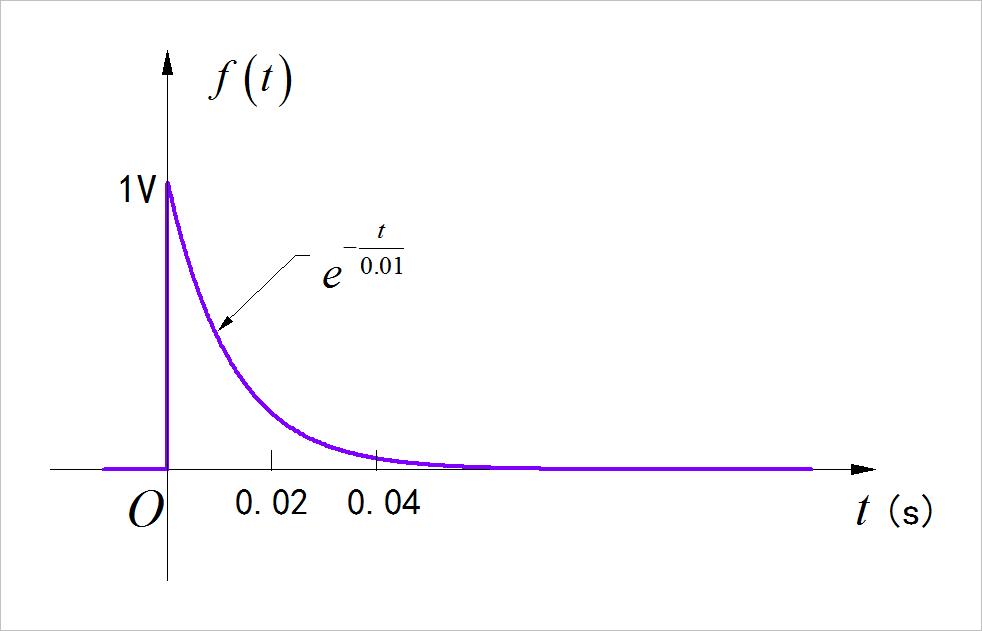
▲ 图1.1.16 信号波形

▲ 图1.1.17 信号波形
(2) sinc函数乘积信号
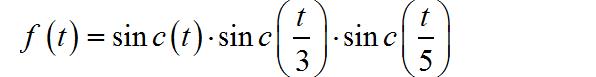
其中: sin c ( t ) = sin ( t ) / t \\sin c\\left( t \\right) = \\sin \\left( t \\right)/t sinc(t)=sin(t)/t 。
◎ 解答:
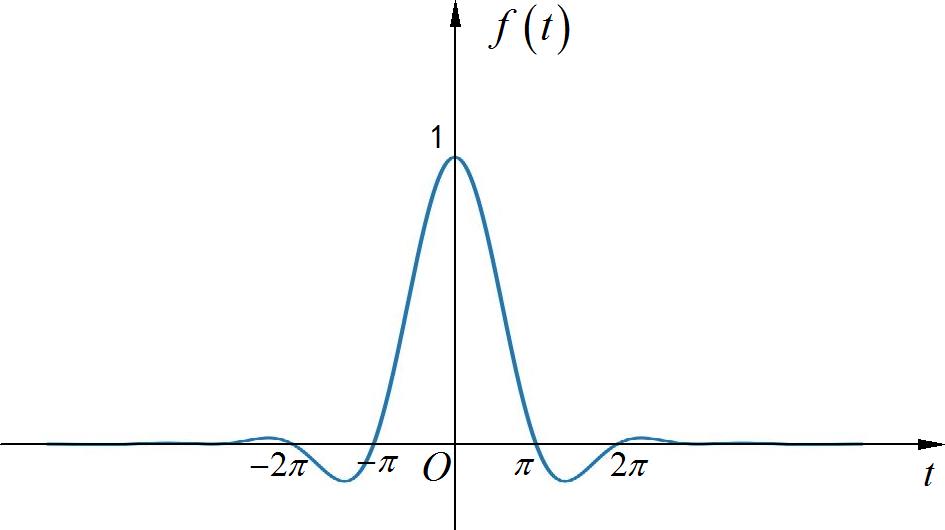
▲ 图1.1.18 信号波形

▲ 图1.1.19 信号波形
(3)震荡序列信号

注意:序列函数中的自变量是 n n n 的平方。请观察序列,并判断该序列是否为周期序列信号?
◎ 解答:
该序列信号是一个周期为 6 的周期序列信号。
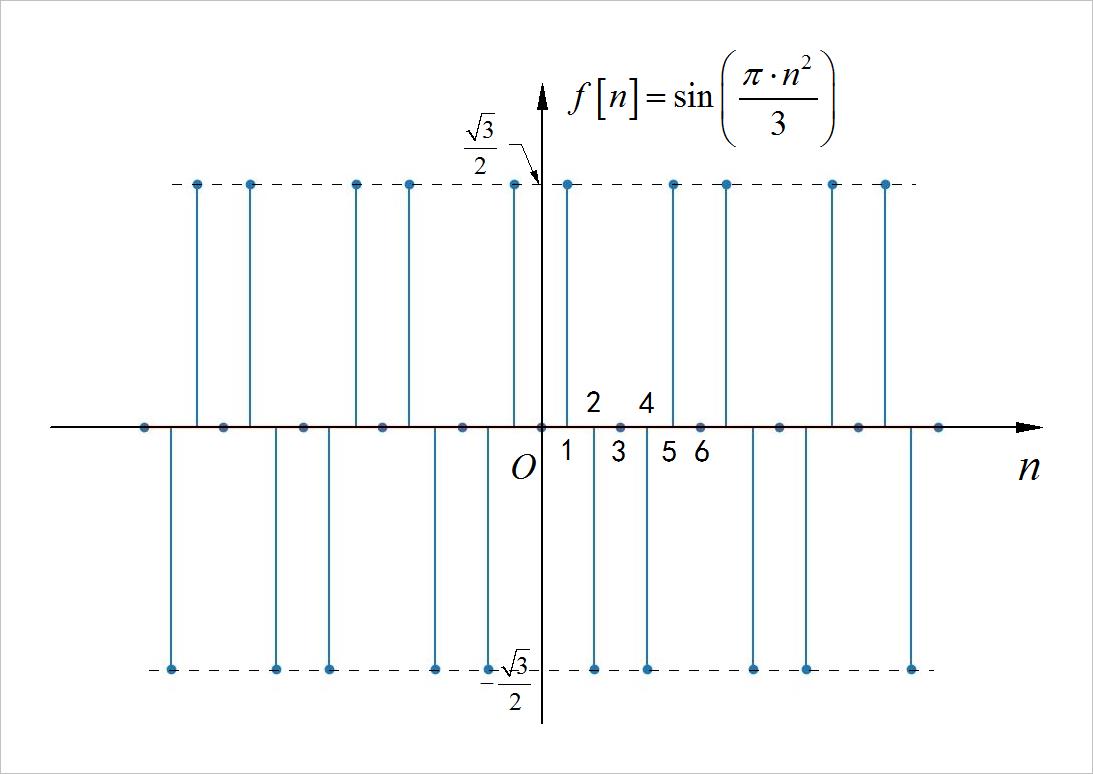
▲ 图1.1.20 信号波形
◎ 解答:
(4) 具有无限多个极大值极小值的有限长信号

这个函数具有无穷多个极大值,极小值。在博文 傅里叶变换中的狄利克雷条件 分析了它的傅里叶变换的特点。

▲ 图1.1.21 信号波形
◎ 解答:
(5)波形发散的周期信号
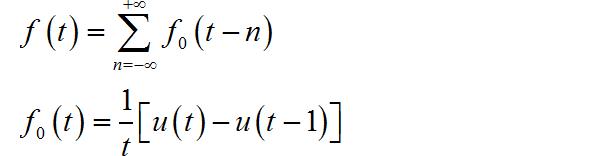
提示:这个周期信号将来会在傅里叶变换的狄利克雷条件中分析。在博文 傅里叶变换中的狄利克雷条件 分析了它的傅里叶变换的特点。也请大家思考一下,这个函数在单个周期内:
- 面积是否有限?
- 能量是否有限?
◎ 解答:
该信号周期内的面积无限大, 能量是无限大。
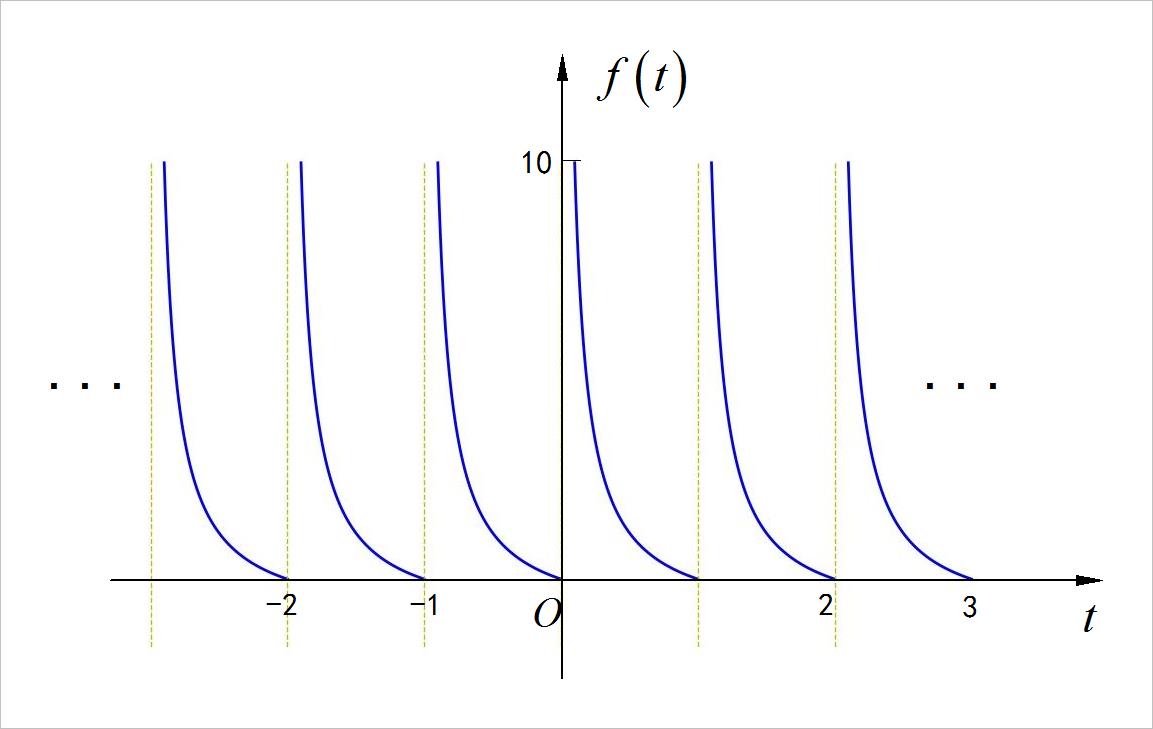
▲ 图1.1.22 信号波形
from headm import *
t = linspace(0.1, 1, 100)
ft = 1/t
for n in range(6):
nn = n - 3
tt = t + nn
plt.plot(tt, ft, 'b-', linewidth=2)
tn = (nn, nn)
yn = (10, -0.5)
plt.plot(tn, yn, 'y--', linewidth=1)
plt.xlabel("t")
plt.ylabel("f(t)")
plt.tight_layout()
plt.show()
二、写出信号函数表达式
根据下面信号的波形,写出对应的函数表达式。注意,同样一个波形可能会存在多种等效的函数表达式。
1、必做题
(1)三角信号
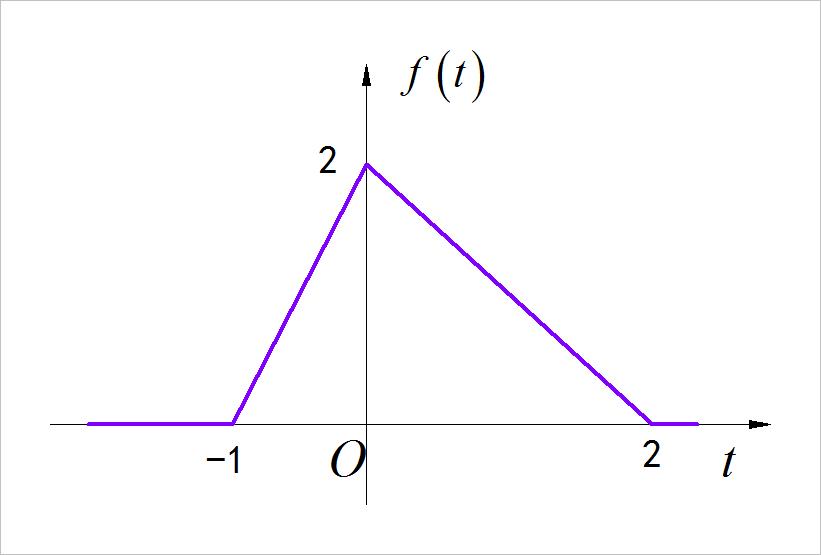
▲ 图1.2.1 三角信号
◎ 解答:
(1)使用分段形式表示的函数形式:

(2)使用单位阶跃函数表示的函数形式:

下面使用Python 程序绘制上述函数,可以验证所得到的结果是正确的。
from headm import *
def f(t):
return 2*(t+1)*heaviside(t+1, 0.5) - 3*t*heaviside(t, 0.5) + (t-2)*heaviside(t-2, 0.5)
t = linspace(-3, 3, 10000)
ft = f(t)
plt.plot(t, ft, linewidth=2)
plt.xlabel('n')
plt.ylabel("f[n]")
plt.axis([-3.5, 3.5, -0.5, 3])
plt.tight_layout()
plt.show()
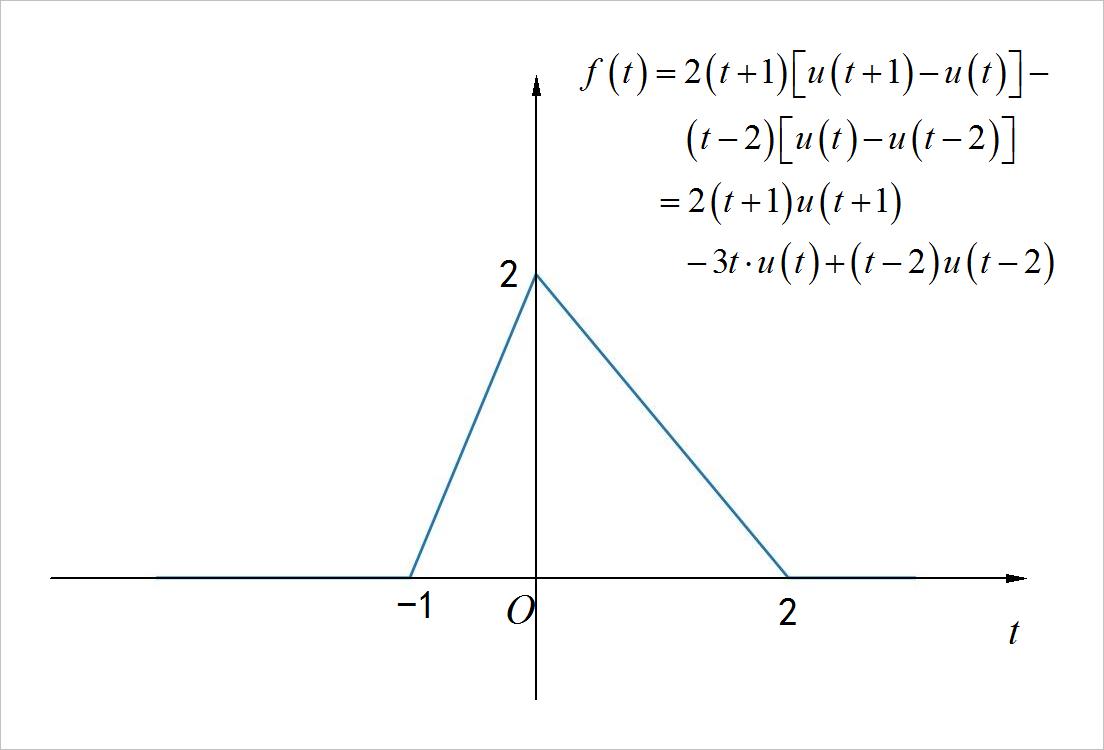
▲ 图A1.2.2 使用程序绘制的函数波形
(2)分段阶跃信号
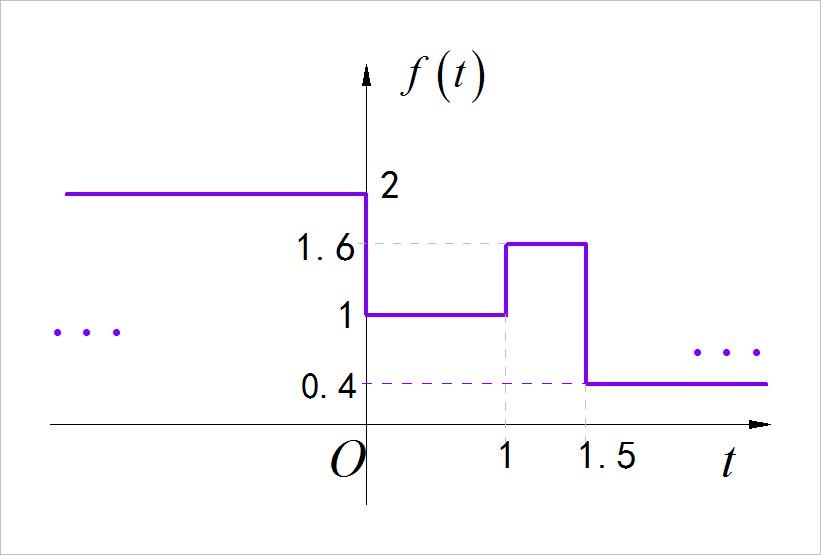
▲ 图1.2.2 分段阶跃信号
◎ 解答:
注:这个函数图像,在最初作业内容发布的时候,最后一段直线的高度没有给定。 这里给定的答案是将其高度设定为 0.4 进行求解。

(3)左边正弦信号
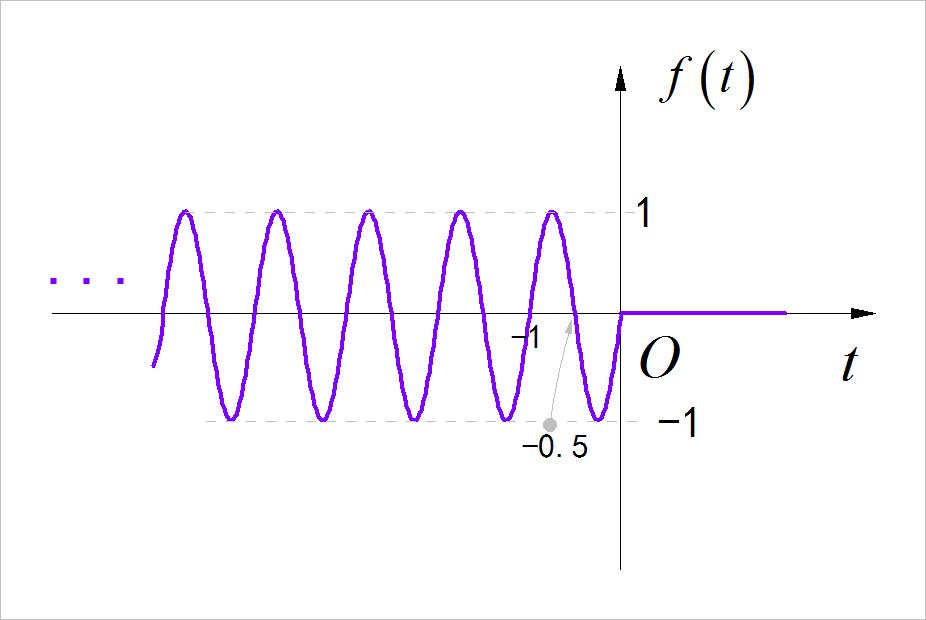
▲ 图1.2.4 左边正弦信号
注意:在 t > 0 t > 0 t>0 时,对应的 f ( t ) = 0 f\\left( t \\right) = 0 f(t)=0 。信号波形往左无限延拓。
◎ 解答:

(4)单边指数衰减振荡信号
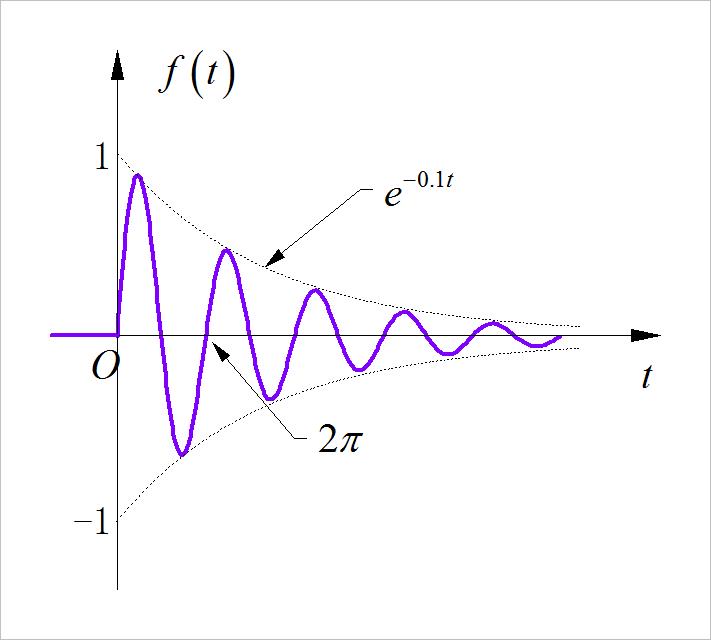
▲ 图1.2.5 单边指数衰减振荡信号
◎ 解答:
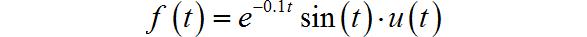
from headm import *
def f(t):
return exp(-0.1*t)*sin(t)*heaviside(t,0.5)
t = linspace(-1, 40, 10000)
ft = f(t)
up = exp(-0.1*t)*heaviside(t, 0.5)
dn = -up
plt.plot(t, ft, linewidth=2)
plt.plot(t, up, 'k--', linewidth=1)
plt.plot(t, dn, 'k--', linewidth=1)
plt.xlabel('n')
plt.ylabel("f[n]")
plt.tight_layout()
plt.show()

▲ 图A1.2.6 利用Python 绘制的图像
2、选做题
(1) 周期方波信号
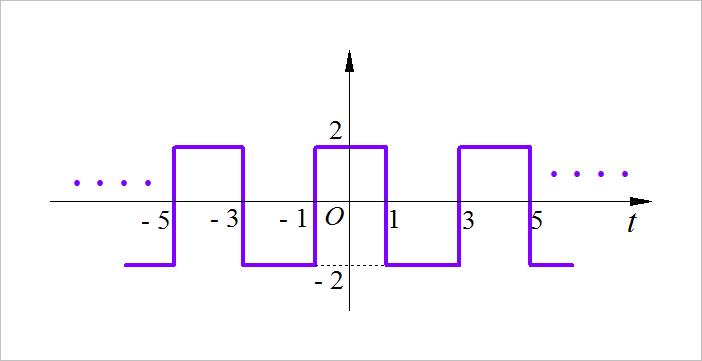
▲ 图1.2.6 周期方波信号
提示:参考前面绘制信号波形中的“复合函数”,以及应用 u ( t ) u\\left( t \\right) u(t) 的特点。
◎ 解答:
使用复合函数来表述, 但这种形式不太适合用于后期的数学分析。

def f(t):
return 4*heaviside(cos(0.5*pi*t),0.5)-2

▲ 图1.2.8 使用Python绘制的信号图形
利用窗口信号表示成周期信号,这种表示可以比较方便后期的信号分析。

其它参考函数表示形式:
(1)

(2)

(2) 阶跃衰减信号
下面是一个阶跃衰减信号,它:
- 只在 ( 0 , 1 ) \\left( 0,1 \\right) (0,1) 之间取值;
- 起始值 f ( 0 ) = 1 f\\left( 0 \\right) = 1 f(0)=1 ,终值 f ( t ) = 0 , t ≥ 1 f\\left( t \\right) = 0,t \\ge 1 f(t)=0,t≥1 ;
- 从0到1过程中,每前进剩余距离一半幅值就降低一半。

▲ 图1.2.7 阶跃衰减信号
◎ 解答:
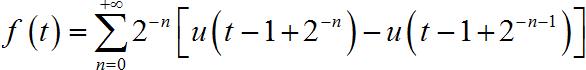
t = linspace(-.25, 1.25, 10000)
ft = t*0
for n in range(100):
ft = ft + 0.5**n*(heaviside(t-1+0.5**n,0)-heaviside(t-1+0.5**(n+1),0))

▲ 图1.2.10 使用Python绘制的信号波形
三、判断信号的周期性
1、必做题
(1) 正弦信号叠加

◎ 解答: 非周期信号。

▲ 图1.3.1 信号的波形
(2) 复指数调制信号

◎ 解答: 周期信号, 周期为4
π
\\pi
π 。
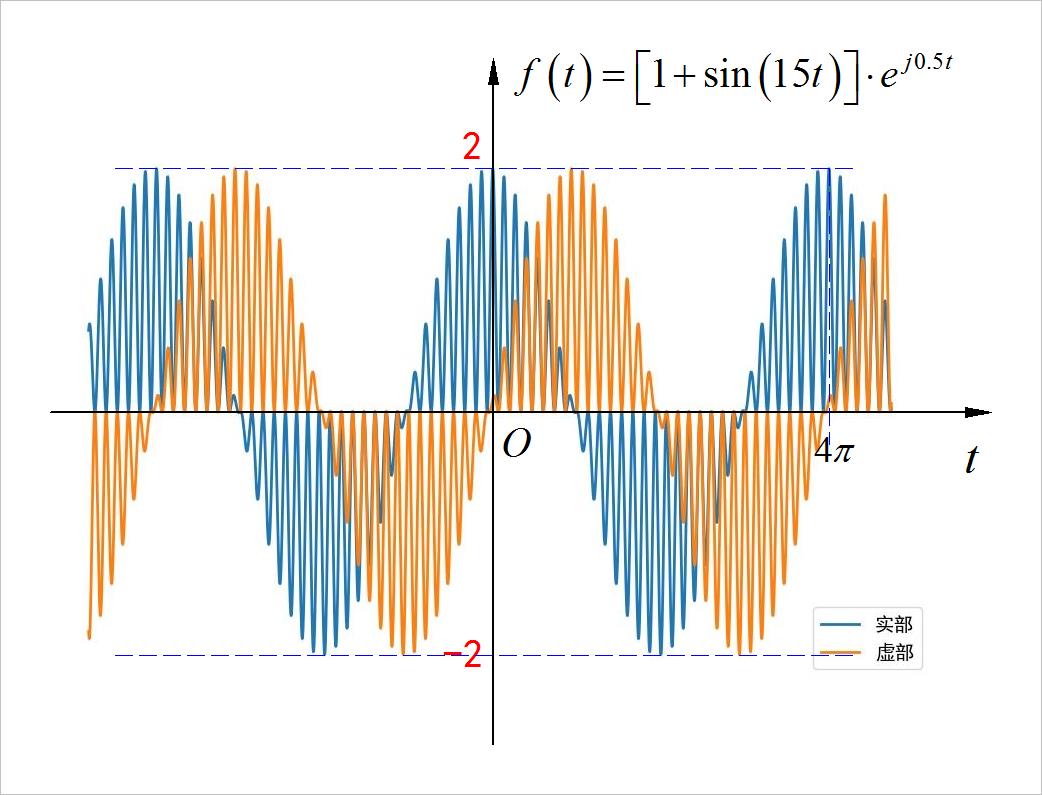
▲ 图1.3.2 信号的波形
(3) 方波信号

◎ 解答: 周期信号, 周期为2T。
def f(t):
v = t*0
for n in range(-40, 40):
v = v + (-1)**n*(heaviside(t-n,0)-heaviside(t-n-1,0))
return v
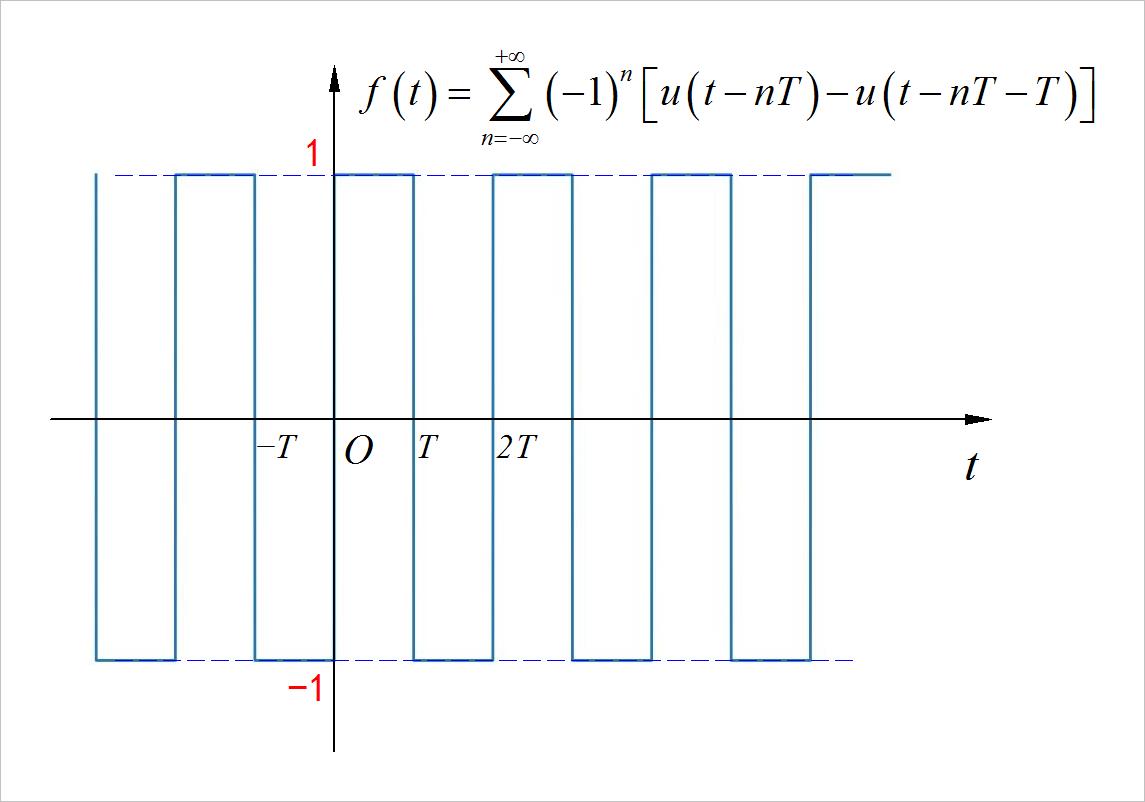
▲ 图1.3.3 信号的波形
(4) 正弦信号三次方

◎ 解答: 周期信号, 周期为 1。
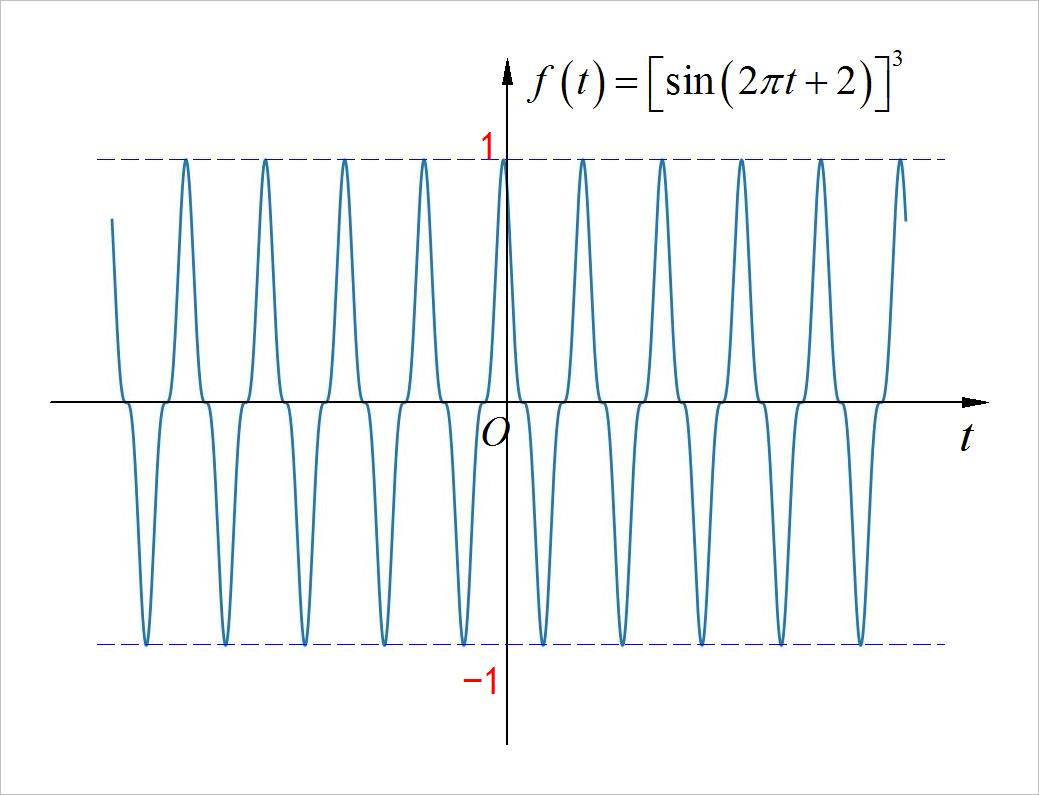
▲ 图1.3.4 信号的波形
(5) 自变量三次方正弦信号
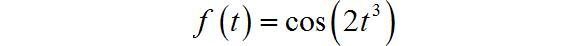
◎ 解答: 非周期信号。

▲ 图1.3.5 信号的波形
(6)自变量三次方的正弦波序列
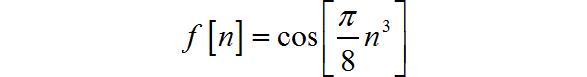
◎ 解答: 周期序列信号, 周期为 16。

▲ 图1.3.6 序列的波形
2、选做题
(1) 斜边信号与振荡信号的叠加
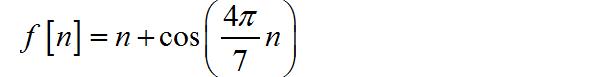
◎ 解答: 非周期信号。

▲ 图1.3.7 序列的波形
(2)判断题
◎ 解答
- 非周期信号与周期信号叠加一定是周期信号。( × )
- 周期信号与周期信号叠加一定是周期信号。( × )
(3)判断题
已知两个序列之间满足
y
[
n
]
=
x
[
2
n
]
y\\left[ n \\right] = x\\left[ 2n \\right]
y[n]=x[2n] 。请问:
- 如果 y [ n ] y\\left[ n \\right] y[n] 是周期信号,那么 x [ n ] x\\left[ n \\right] x[n] 是否也是周期信号?
- 如果 x [ n ] x\\left[ n \\right] x[n] 是周期信号,那么 y [ n ] y\\left[ n \\right] 以上是关于信号与系统 2023(春季) 作业参考答案 - 第一次作业的主要内容,如果未能解决你的问题,请参考以下文章