夜深人静写算法(三十七)- 威尔逊定理
Posted 英雄哪里出来
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了夜深人静写算法(三十七)- 威尔逊定理相关的知识,希望对你有一定的参考价值。
一、前言
欧拉定理、费马小定理、中国剩余定理 我们都(假设)已经学会了。那么今天的这个定理,是非常重要的。因为只有学会了它,你才能凑齐数论四大定理。
没错,这个定理考试不会考,ACM 基本很少遇到(遇到过三道题),LeetCode 上没有,面试官也不会问,它叫 威尔逊定理。所以建议这篇文章,能不看就不看,基本是在浪费时间。实在想看,我也不会阻拦。
当然,无论有没有读者,我都会继续更新,因为我就是我,我只是单纯的想要凑齐数论 四大定理:欧拉定理、费马小定理、中国剩余定理、威尔逊定理。
二、威尔逊定理
1、定义
- ( p − 1 ) ! ≡ − 1 ( m o d p ) (p-1)! \\equiv -1(mod \\ p) (p−1)!≡−1(mod p) 是 p p p 为素数 的 充分必要条件。
2、充分性
- 对于
p
p
p 不是素数的情况,我们分成以下几种情况来讨论:
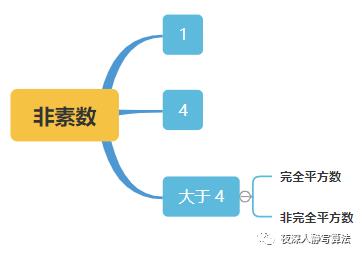
- 当 p = 1 p=1 p=1 时,直接带入, ( 1 − 1 ) ! ≡ 0 ( m o d 1 ) (1-1)! \\equiv 0(mod \\ 1) (1−1)!≡0(mod 1);
- 当 p = 4 p=4 p=4 时,直接带入, ( 4 − 1 ) ! ≡ 2 ( m o d 4 ) (4-1)! \\equiv 2(mod \\ 4) (4−1)!≡2(mod 4);
- 当 p > 4 p \\gt 4 p>4 时:
a)当 p p p 是 完全平方数
- 则 p = k 2 p = k^2 p=k2,由于 p > 4 p > 4 p>4,则 k > 2 k > 2 k>2;
- 然后,我们比较以下 2 k 2k 2k 和 p p p 的大小,即:
- 2 k − p = 2 k − k 2 = 2 k − k 2 − 1 + 1 = − ( k − 1 ) 2 + 1 < 0 \\begin{aligned}2k - p &= 2k - k^2 \\\\ &= 2k - k^2 - 1 + 1 \\\\ &= -(k-1)^2 + 1 \\lt 0\\end{aligned} 2k−p=2k−k2=2k−k2−1+1=−(k−1)2+1<0
- 于是有 k < p k \\lt p k<p, 2 k < p 2k \\lt p 2k<p 成立。
- ( p − 1 ) ! = 1 × 2 × . . . × k × . . . × 2 k × . . . ( p − 1 ) = k × 2 k × n = 2 n k 2 = 2 n p \\begin{aligned}(p-1)! &= 1 \\times 2 \\times ... \\times k \\times ... \\times 2k \\times ... (p-1) \\\\ &= k \\times 2k \\times n \\\\ &= 2n k^2 \\\\ &= 2np \\end{aligned} (p−1)!=1×2×...×k×...×2k×...(p−1)=k×2k×n=2nk2=2np
- 所以有:
- ( p − 1 ) ! ≡ 0 ( m o d p ) (p-1)! \\equiv 0(mod \\ p) (p−1)!≡0(mod p)
b)当 p p p 不是 完全平方数
- 那么, p p p 必然等于两个完全不相等的数 a a a 和 b b b 的乘积,不妨设 a < b a \\lt b a<b,则满足:
- 1 < a < b < p 1 \\lt a \\lt b \\lt p 1<a<b<p
- ( p − 1 ) ! = 1 × 2 × . . . × a × . . . × b × . . . ( p − 1 ) = a × b × n = n a b = n p \\begin{aligned}(p-1)! &= 1 \\times 2 \\times ... \\times a \\times ... \\times b \\times ... (p-1) \\\\ &= a \\times b \\times n \\\\ &= nab \\\\ &= np \\end{aligned} (p−1)!=1×2×...×a×...×b×...(p−1)=a×b×n=nab=np
- 所以有:
- ( p − 1 ) ! ≡ 0 ( m o d p ) (p-1)! \\equiv 0(mod \\ p) (p−1)!≡0(mod p)
3、必要性
- 当 p p p 为素数时,考虑二次剩余式:
- x 2 ≡ 1 ( m o d p ) x^2 \\equiv 1(mod \\ p) x2≡1(mod p)
- 移项得到 x 2 − 1 ≡ 0 ( m o d p ) x^2-1 \\equiv 0(mod \\ p) x2−1≡0(mod p)
- 分解因式得到:
- ( x − 1 ) ( x + 1 ) ≡ 0 ( m o d p ) (x-1)(x+1) \\equiv 0(mod \\ p) (x−1)(x+1)≡0(mod p)
- 从而可得:
- x ≡ 1 ( m o d p ) x \\equiv 1(mod \\ p) x≡1(mod p) 或者 x ≡ p − 1 ( m o d p ) x \\equiv p-1(mod \\ p) x≡p−1(mod p)
- 那么我们抛开 1 1 1 和 p − 1 p-1 p−1 这两个数不管,对于 a ∈ [ 2 , p − 2 ] a \\in [2, p-2] a∈[2,p−2],必然存在一个和它不相等的逆元 a − 1 ∈ [ 2 , p − 2 ] a^{-1} \\in [2, p-2] a−1∈[2,p−2],满足:
- a a − 1 ≡ 1 ( m o d p ) aa^{-1} \\equiv 1(mod \\ p) aa−1≡1(mod p)
- 所以必然有 ( p − 3 ) 2 \\frac {(p-3)} {2} 2(p−3)以上是关于夜深人静写算法(三十七)- 威尔逊定理的主要内容,如果未能解决你的问题,请参考以下文章
