leetcode 474. 一和零

Posted 2021-05-29 大忽悠爱忽悠

---

一和零题解集合

• 动态规划----01背包问题
• 滚动数组优化
• 一维优化
• 总结
• 记忆化搜索
• 总结

---

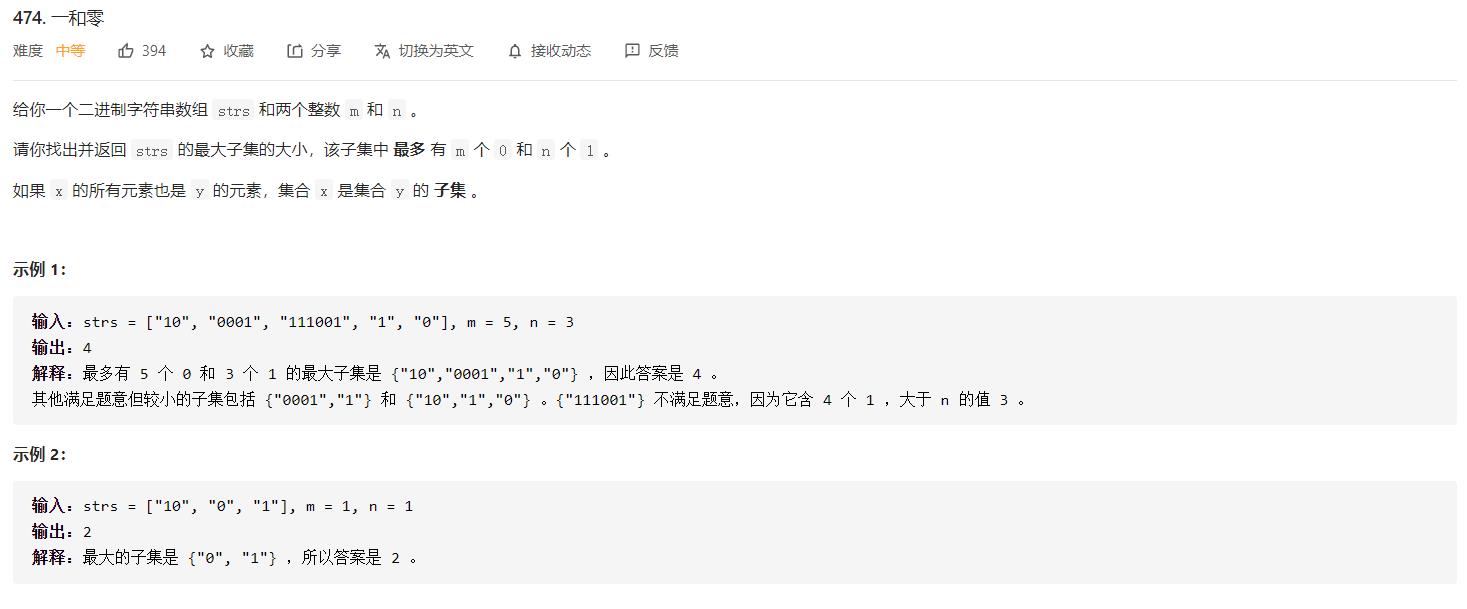
动态规划----01背包问题

来说题，本题不少同学会认为是多重背包，一些题解也是这么写的。

其实本题并不是多重背包，再来看一下这个图，捋清几种背包的关系

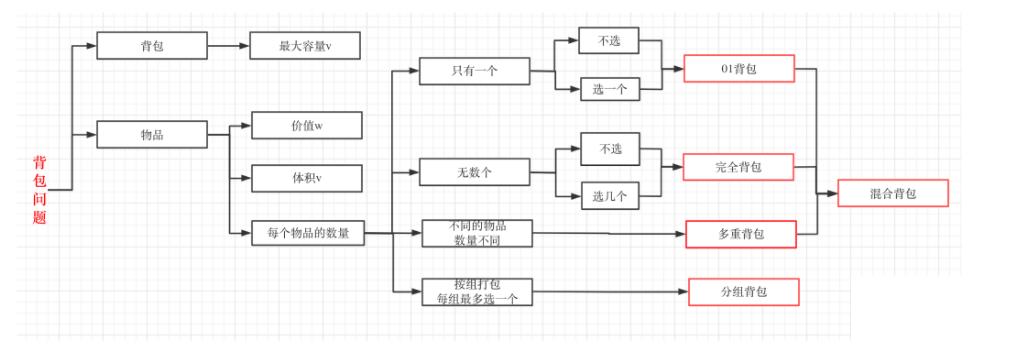
多重背包是每个物品，数量不同的情况。

本题中strs 数组里的元素就是物品，每个物品都是一个字符串

而m 和 n相当于是一个背包，两个维度的背包。

理解成多重背包的同学主要是把m和n混淆为物品了，感觉这是不同数量的物品，所以以为是多重背包。

但本题其实是01背包问题！

这不过这个背包有两个维度，一个是m 一个是n，而不同长度的字符串就是不同大小的待装物品。

---

思路：把总共的 0 和 1 的个数视为背包的容量，每一个字符串视为装进背包的物品。这道题就可以使用 0-1 背包问题的思路完成，这里的目标值是能放进背包的字符串的数量。

动态规划的思路是：物品一个一个尝试，容量一点一点尝试，每个物品分类讨论的标准是：选与不选。

定义状态：尝试题目问啥，就把啥定义成状态。dp[i][j][k] 表示输入字符串在子区间 [0, i] 能够使用 j 个 0 和 k 个 1 的字符串的最大数量。

状态转移方程：

初始化：

为了避免分类讨论，通常多设置一行。这里可以认为，第 0 个字符串是空串。第 0 行默认初始化为 0。

输出：

输出是最后一个状态，即：dp[len][m][n]。

代码:

class Solution {
public:
	int findMaxForm(vector<string>& strs, int m, int n) 
	{
		int len = strs.size();
		//第一行已经进行了初始化，都初始化为0
		//即当我们什么物品(字符串)都不考虑的时候，背包中0和1的个数都是0
		vector<vector<vector<int>>> dp(len + 1, vector<vector<int>>(m + 1, vector<int>(n + 1, 0)));
	    //考虑其他物品
		for (int i = 1; i <= len; i++)//物品遍历
		{
			for (int j = 0; j <= m; j++)//0个数容量遍历
			{
				for (int k = 0; k <= n; k++)//1个数容量遍历
				{
					//不选择当前物品
					dp[i][j][k] = dp[i - 1][j][k];
					//选择当前物品
					//计算当前选择物品中0和1的个数
					int zero = count(strs[i - 1].begin(), strs[i - 1].end(), '0');
					int one = count(strs[i - 1].begin(), strs[i - 1].end(), '1');
					if (j >= zero && k >= one)
						dp[i][j][k] = max(dp[i-1][j][k], dp[i - 1][j - zero][k - one]+1);
				}
			}
		}
		return dp[len][m][n];
	}
};

---

滚动数组优化

因为求解当前行只依赖与上一行，因此可以把行数压缩到两行

代码:

class Solution {
public:
	int findMaxForm(vector<string>& strs, int m, int n) 
	{
		int len = strs.size();
		//第一行已经进行了初始化，都初始化为0
		//即当我们什么物品(字符串)都不考虑的时候，背包中0和1的个数都是0
		vector<vector<vector<int>>> dp(2, vector<vector<int>>(m + 1, vector<int>(n + 1, 0)));
	    //考虑其他物品
		for (int i = 1; i <= len; i++)//物品遍历
		{
			for (int j = 0; j <= m; j++)//0个数容量遍历
			{
				for (int k = 0; k <= n; k++)//1个数容量遍历
				{
					//不选择当前物品
					dp[i&1][j][k] = dp[(i - 1)&1][j][k];
					//选择当前物品
					//计算当前选择物品中0和1的个数
					int zero = count(strs[i - 1].begin(), strs[i - 1].end(), '0');
					int one = count(strs[i - 1].begin(), strs[i - 1].end(), '1');
					if (j >= zero && k >= one)
						dp[i&1][j][k] = max(dp[(i-1)&1][j][k], dp[(i - 1)&1][j - zero][k - one]+1);
				}
			}
		}
		return dp[len&1][m][n];
	}
};

---

一维优化

动规五部曲：

1.确定dp数组（dp table）以及下标的含义

dp[i][j]：最多有i个0和j个1的strs的最大子集的大小为dp[i][j]。

2.确定递推公式

dp[i][j] 可以由前一个strs里的字符串推导出来，strs里的字符串有zeroNum个0，oneNum个1。

dp[i][j] 就可以是 dp[i - zeroNum][j - oneNum] + 1。

然后我们在遍历的过程中，取dp[i][j]的最大值。

所以递推公式：dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);

此时大家可以回想一下01背包的递推公式：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

对比一下就会发现，字符串的zeroNum和oneNum相当于物品的重量（weight[i]），字符串本身的个数相当于物品的价值（value[i]）。

这就是一个典型的01背包！ 只不过物品的重量有了两个维度而已。

3.dp数组如何初始化

01背包的dp数组初始化为0就可以。

因为物品价值不会是负数，初始为0，保证递推的时候dp[i][j]不会被初始值覆盖。

4.确定遍历顺序

在把01背包问题的底裤扒个底朝天！！！中，我们讲到了01背包为什么一定是外层for循环遍历物品，内层for循环遍历背包容量且从后向前遍历！

那么本题也是，物品就是strs里的字符串，背包容量就是题目描述中的m和n。

代码:

	    //考虑其他物品
		for (int i = 1; i <= len; i++)//物品遍历
		{
			//选择当前物品
             //计算当前选择物品中0和1的个数
			int zero = count(strs[i - 1].begin(), strs[i - 1].end(), '0');
			int one = count(strs[i - 1].begin(), strs[i - 1].end(), '1');
			for (int j = m; j>=zero; j--)//0个数容量遍历
			{
				for (int k =n; k>=one; k--)//1个数容量遍历
				{
						dp[j][k] = max(dp[j][k], dp[j - zero][k - one]+1);
				}
			}
		}
		return dp[m][n];
	}

有同学可能想，那个遍历背包容量的两层for循环先后循序有没有什么讲究？

没讲究，都是物品重量的一个维度，先遍历那个都行！

5.举例推导dp数组

以输入：[“10”,“0001”,“111001”,“1”,“0”]，m = 3，n = 3为例

最后dp数组的状态如下所示：

代码:

class Solution {
public:
	int findMaxForm(vector<string>& strs, int m, int n) 
	{
		int len = strs.size();
		//第一行已经进行了初始化，都初始化为0
		//即当我们什么物品(字符串)都不考虑的时候，背包中0和1的个数都是0
		vector<vector<int>> dp(vector<vector<int>>(m + 1, vector<int>(n + 1, 0)));
	    //考虑其他物品
		for (int i = 1; i <= len; i++)//物品遍历
		{
			//选择当前物品
             //计算当前选择物品中0和1的个数
			int zero = count(strs[i - 1].begin(), strs[i - 1].end(), '0');
			int one = count(strs[i - 1].begin(), strs[i - 1].end(), '1');
			for (int j = m; j>=zero; j--)//0个数容量遍历
			{
				for (int k =n; k>=one; k--)//1个数容量遍历
				{
						dp[j][k] = max(dp[j][k], dp[j - zero][k - one]+1);
				}
			}
		}
		return dp[m][n];
	}
};

---

总结

不少同学刷过这道提，可能没有总结这究竟是什么背包。

这道题的本质是有两个维度的01背包，如果大家认识到这一点，对这道题的理解就比较深入了。

---

记忆化搜索

这里还是把问题转化为对多叉树的遍历，但这里是针对每个字符串选与不选的抉择，因此可以看成对二叉树的遍历

不理解的可以看下面的图片:

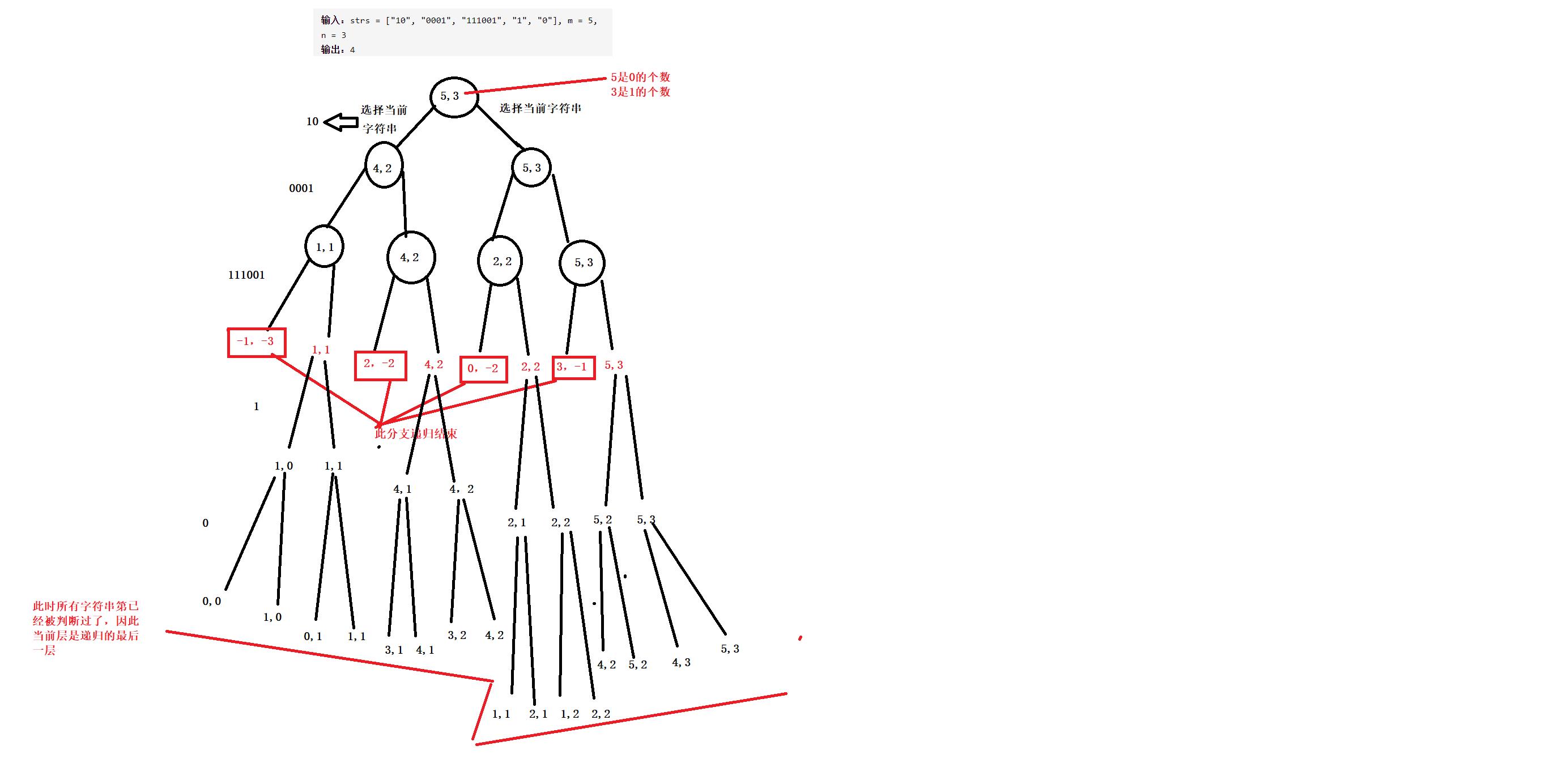
下面给出递归三部曲

1.结束条件

当前分支m或者n的值小于0

当前字符数组里面所有字符串都被使用过了

2.返回值

返回当前所使用的的字符串个数

3，本级递归做什么

计算选取当前字符串与不选取当前字符串，两个选择中，字符串使用个数较大者

代码:

class Solution {
public:
	int findMaxForm(vector<string>& strs, int m, int n) 
	{
		return dfs(strs, m, n, 0);
	}
	int dfs(vector<string>& strs, int m, int n, int index)//index记录当前遍历到了第几个字符串 
	{
		if (m <0 || n <0|| index == strs.size()) return 0;
		int zero = count(strs[index].begin(), strs[index].end(), '0');
		int one = count(strs[index].begin(), strs[index].end(), '1');
		if (m - zero >= 0 && n - one >= 0)//当前字符串能选择的前提是满足m和n的限制条件
			return max(dfs(strs, m - zero, n - one, index + 1) + 1, dfs(strs, m, n, index + 1));
		else
			return dfs(strs, m, n, index + 1);
	}
};

显然这里计算还是可以计算出来的，但是超时了很多，还是需要用哈希表保存计算结果，防止重复计算

在递归过程中会遇到重叠子问题 如

f(8,5,4) = max(f(7,5,4),f(7,3,2)) str = 1100
f(8,5,2) = max(f(7,5,2),f(7,3,2)) str = 11

f(7,3,2) 会被重复计算

所以可添加记忆化搜索

代码

class Solution {
	unordered_map<string, int> cache;
public:
	int findMaxForm(vector<string>& strs, int m, int n) 
	{
		return dfs(strs, m, n, 0);
	}
	int dfs(vector<string>& strs, int m, int n, int index)//index记录当前遍历到了第几个字符串 
	{
		string temp = to_string(m) +'+' +to_string(n)+'+' + to_string(index);
		if (cache.find(temp) != cache.end()) return cache[temp];
		if (m <0 || n <0|| index == strs.size()) return 0;
		int zero = count(strs[index].begin(), strs[index].end(), '0');
		int one = count(strs[index].begin(), strs[index].end(), '1');
		if (m - zero >= 0 && n - one >= 0)//当前字符串能选择的前提是满足m和n的限制条件
			return cache[temp]=max(dfs(strs, m - zero, n - one, index + 1) + 1, dfs(strs, m, n, index + 1));
		else
			return cache[temp]=dfs(strs, m, n, index + 1);
	}
};

---

总结

这道题的c++记忆化搜索如果有好的剪枝优化方法，可以在评论区分享一下