leetcode No474. 一和零 java

Posted 2021-07-11 短腿Cat

目录

• 前言
• 背包问题
• 题目
• 分析

---

前言

这道题其实是背包问题的“升级版”，因此我就先来介绍一下背包问题，然后再来看这道题，下面我先说说背包问题的解法：

---

背包问题

有n个物品，它们有各自的体积和价值，现有给定容量的背包，如何让背包里装入的物品具有最大的价值总和？
eg：number＝4，capacity＝8

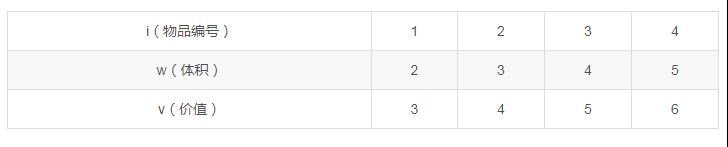
w数组代表该编号物品体积，v代表该编号物品的价值

做一道dp题,第一步就是确定dp数组维度，以哪些作为维度，边界问题，我定义背包容量为一个维度，物品数量为一个维度，因为令物品有0状态和令背包容量可为0的话方便考虑边界，则dp定义为：
dp[capacity + 1][number + 1]
边界为：物品 i 从0到number，容量 j 从0到capacity
初始化边界，物品为0个的时候背包能装的价值是多少（为0），背包容量为0的时候，价值为多少（为0）即：dp[i][0] = 0 , dp[0][j] = 0
初始化之后如下图：

1. ：当前物品容量小于背包容量时dp[i][j] = dp[i - 1][j] 。例如：判断i = 1，j = 1的情况，当背包容量为1的时候，编号为1的体积为2，因此编号为1的物品就不可放入背包，则i = 1，j = 1的情况就等于i = 0， j = 1 的情况，如下图：
   
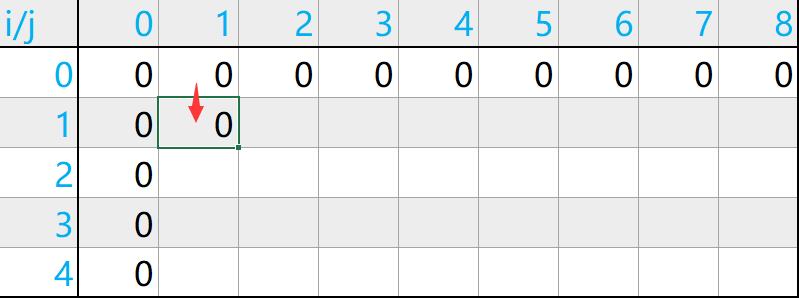
2. 当背包容量大于物品体积时，dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - w[i - 1]] + v[i - 1]) 。其实这里分为两种情况，第一种情况：选择该物品。第二种情况：不选择该物品。
   
   当选择该物品时： w[i - 1]为当前物品体积，因为j是物品总重,j - w[i - 1] 代表除去该物品后剩余的容量，dp[i][j - w[i - 1]]代表除了放该物品之外能放置之前的所有物品的最大价值 , v[i - 1]代表当前物品价值，则dp[i][j - w[i - 1]] + v[i - 1]代表放置了该物品之后的当前最大价值
   当不选择该物品时：dp[i][j] = dp[i - 1][j] 。因为不选择的时候价值和第一种情况是一样的。
   那我们对情况2的总判断又该做什么样的处理呢？应该让放置后的dp与不放置该物品时的dp的值进行比较，最大价值者为该点dp值。
   
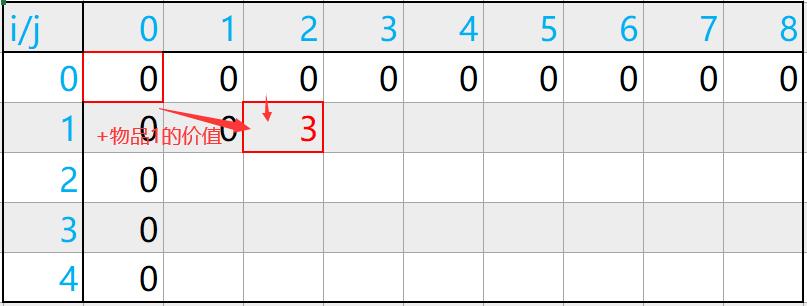
   最后一步判断：
   
   最后一个元素中，dp[i - 1][j - w[i - 1]] + v[i - 1] 的值为在i=3，j=4的情况的dp值，然后加上当前物品的价值（为10）与dp[i - 1][j] = 9比大小，得出答案为10

最终表为：

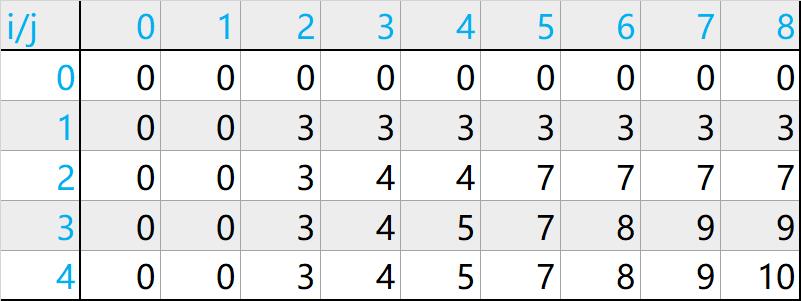
代码如下：

public static void main(String[] args) {
        int[][] dp = new int[5][9];
        int[] w = {2, 3, 4, 5};
        int[] v = {3, 4, 5, 6};
        
        for (int i = 1; i < 5; i++) {
            for (int j = 1; j < 9; j++) {
                if (w[i - 1] > j) {
                    dp[i][j] = dp[i - 1][j];
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - w[i - 1]] + v[i - 1]);
                }
            }
        }
        System.out.println(dp[4][8]);
    }

注：这是dp问题中比较经典的一道题了，所以需要好好掌握

---

然后我们来看本题，为什么说本题是背包问题的“升级版”？

题目

---

分析

我们注意到，其实"物品"就是字符串数组中的每一个"01"字符串，“物品数量”，就是数组的长度；每个物品的体积呢？即0的数量和1的数量。而背包容量呢？这里我们注意，原本背包问题只有“背包容量”一个变量，而本题有’0’ 和 '1’两个变量，所以本题"背包容量"为 0 和 1 这两个
因此我们dp数组也好确定了，根据 “当字符串长度为x，且0的数量不超过y， 1的数量不超过z”这句话，我们将dp数组设定为dp[str.length][m][n]，其他的主要思路就和背包问题一样，不过这里要多提一下，因为计算的是子集元素数量，所以原背包问题里的 ‘价值’ 转换到这道题就是是否计算该元素数量，即v[i]全部都是1，
代码如下：

class Solution {
    public int findMaxForm(String[] strs, int m, int n) {
        int len = strs.length;
        int a = 0, b = 0;
        int[][][] dp = new int[len + 1][m + 1][n + 1];
        for (int i = 1; i <= len; i++) {
            a = getCharNum(strs[i - 1], '0');
            b = getCharNum(strs[i - 1], '1');
            for (int j = 0; j <= m; j++) {
                for (int k = 0; k <= n; k++) {
                    dp[i][j][k] = dp[i - 1][j][k];
                    if (a <= j && b <= k) {
                        dp[i][j][k] = Math.max(dp[i - 1][j][k], dp[i - 1][j - a][k - b] + 1);
                    }
                }
            }
            a = 0;
            b = 0;
        }
        return dp[len][m][n];
    }

    private int getCharNum(String str, char c) {
        int count = 0;
        for (char i : str.toCharArray())
            if (i == c)
                count++;
        return count;
    }
}

---

这就是本题的解法了，喜欢的看客点个赞吧谢谢嗷，今天高考的学习学妹们加油~