LeetCode 474 一和零[二进制 动态规划] HERODING的LeetCode之路

Posted 2021-06-23 HERODING23

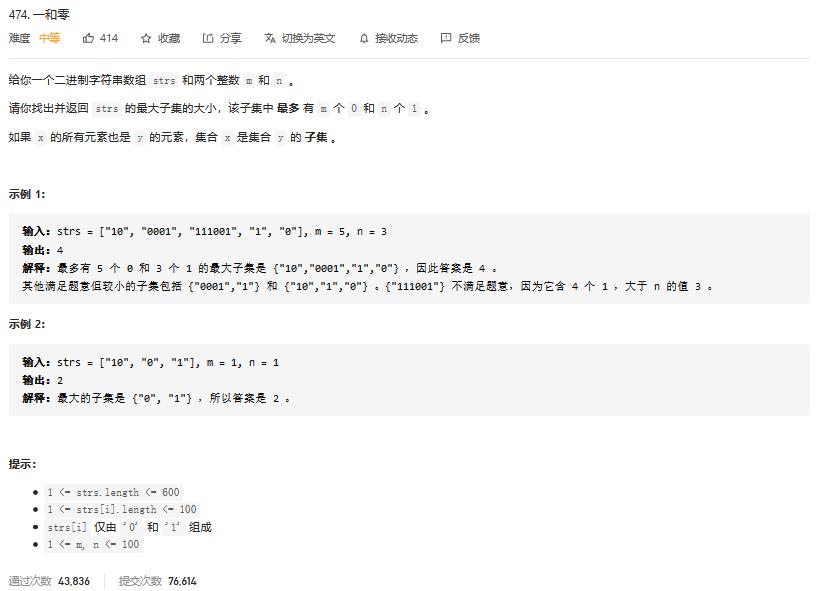解题思路：
经典的0-1背包问题的变形，只不过多了一个维度，解决方法还是一样的，dp[i][j][k]表示前i个字符串满足不超过m个0和n个1的最大长度，代码如下：

class Solution {
public:
    int findMaxForm(vector<string>& strs, int m, int n) {
        int len = strs.size();
        if(len == 0) {
            return 0;
        }
        vector<vector<vector<int>>> dp(len + 1, vector<vector<int>>(m + 1, vector<int>(n + 1)));
        for(int i = 1; i <= len; i ++) {
            int ones = 0, zeros = 0;
            for(char c : strs[i - 1]) {
                if(c == '0') {
                    zeros ++;
                } else {
                    ones ++;
                }
            }
            for(int j = 0; j <= m; j ++) {
                for(int k = 0; k <= n; k ++) {
                    dp[i][j][k] = dp[i - 1][j][k];
                    if(j >= zeros && k >= ones) {
                        dp[i][j][k] = max(dp[i - 1][j][k], 1 + dp[i - 1][j - zeros][k - ones]);
                    }
                }
            }
        }
        return dp[len][m][n];
    }
};

仔细观察代码可以发现，dp[i][][]的计算只和dp[i -1][][]有关，那么很自然用滚动数组的思想来降低空间复杂度，注意要采用倒序遍历的方式，这可以保证转移来的是dp[i-1][][]的值，代码如下：

class Solution {
public:
    int findMaxForm(vector<string>& strs, int m, int n) {
        int len = strs.size();
        if(len == 0) {
            return 0;
        }
        vector<vector<int>> dp(m + 1, vector<int>(n + 1));
        for(int i = 0; i < len; i ++) {
            int ones = 0, zeros = 0;
            for(char c : strs[i]) {
                if(c == '0') {
                    zeros ++;
                } else {
                    ones ++;
                }
            }
            for(int j = m; j >= zeros; j --) {
                for(int k = n; k >= ones; k --) {
                    if(j >= zeros && k >= ones) {
                        dp[j][k] = max(dp[j][k], 1 + dp[j - zeros][k - ones]);
                    }
                }
            }
        }
        return dp[m][n];
    }
};