智能控制导论雪堆博弈-最小节点覆盖问题

Posted 2022-05-02 zstar-_

本篇博文是智能控制导论专业课的实验报告
完整的程序和文档下载地址：https://download.csdn.net/download/qq1198768105/85259200

问题描述

验证结论：当雪堆博弈满足r<1/kmax时(kmax为网络节点的最大度)，网络博弈的纳什均衡中的采用合作策略的节点构成极小节点覆盖。网络结构可自定，节点数目不少于10。

节点的初始状态可随机定为Cooperator或者Defector,按照某种给定顺序(例如1,2,…,10)依次检查每个节点，是否改变其状态可以获得更大收益，如果是则改变状态，否则不改变，直到所有节点都不再改变状态为止。验证合作的节点集合是否是极小节点覆盖。

问题背景

极小节点覆盖

网络节点最小覆盖问题(MVCP)是一个著名组合优化问题，其目的在于找出给定网络的最小节点集合以覆盖所有的边。其中，若节点集合中去掉任何一个点，就不能覆盖网络所有边，则称此时为极小节点覆盖。

雪堆博弈

雪堆博弈所描述的情景是：在一个风雪交加的夜晚，两人相向而来，被一个雪堆所阻。他们可以选择下车铲雪(合作C)，或者都不铲雪(背叛D)。如果两人都不铲雪，两人就都无法通行；如果一人铲雪一人不铲，则铲雪者付出了劳动，背叛者白占了成果。

设铲雪所需的劳动价值为r，通行所获得的收益为1，则雪堆博弈的收益矩阵收益矩阵如下表所示

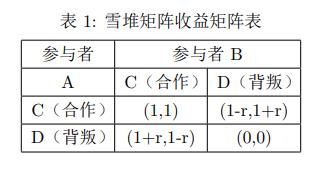
纳什均衡指的是在给定别人策略的情况下，没有人愿意单方面改变自己的策略，从而打破这种均衡。

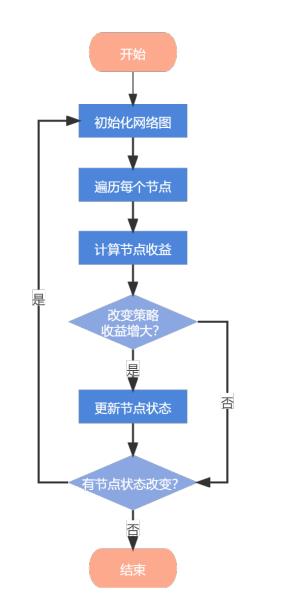
算法思路

为了寻找到当前网络博弈的纳什均衡，需完成以下几个步骤:

1. 随机给每个节点初始状态设置为C或D(C表示合作，D表示背叛)

2. 依次对每个节点计算其采用C或者D的收益，改变其策略使其收益最大

3. 重复2过程到每个节点的状态不在改变

算法流程如图1所示：

实验步骤

网络结构图

本实验网络设置了15个节点，其结构图如图2所示：

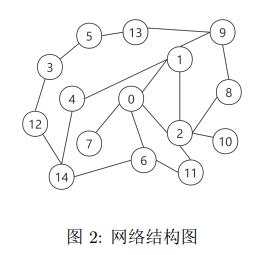
该网络中kmax为5，定理存在条件r<1/kmax，因此实验设定r为0.1。

第一次求解

首先初始化网络，每个节点都有50%的概率选择合作©或背叛(D)，之后根据算法流程进行更新，初始状态，中间过程，最终结果如下图所示：

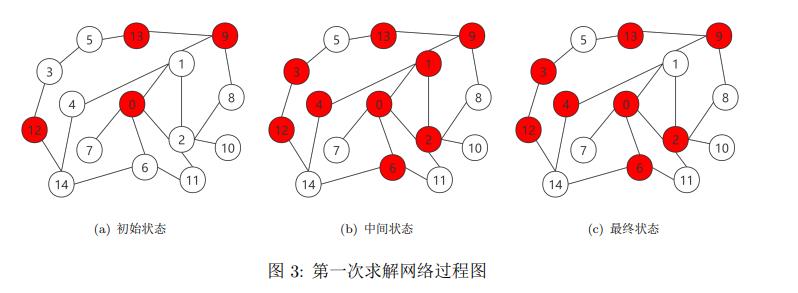
图中，红色代表决策C，白色代表决策D。可以发现，最终结果实现了极小节点覆盖。各节点的决策收益如表2所示：

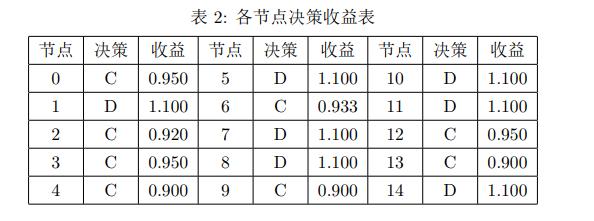
第二次求解

第二次求解过程和第一次类似，初始状态，中间过程，最终结果如下图所示：

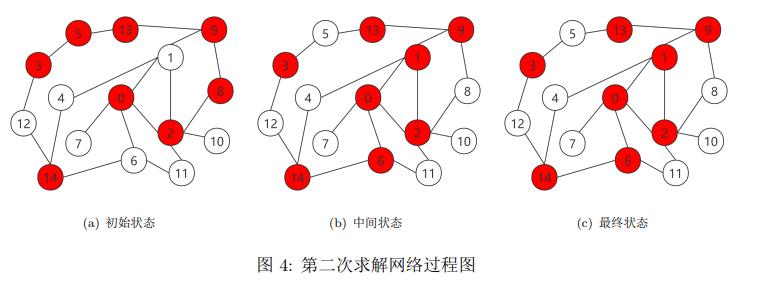
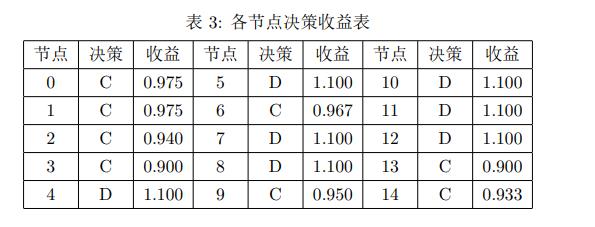
可以发现，由于初始生成情况较好，此次求解很快，中间状态和最终状态一致。同样，和第一次求解对比，可以发现极小节点覆盖的解不唯一，存在多解情况。各节点的决策收益如表3所示：

总结

本次实验验证了结论：当雪堆博弈满足r<1/kmax时(kmax为网络节点的最大度)，网络博弈的纳什均衡中的采用合作策略的节点构成极小节点覆盖。与此同时，该验证过程还反映出个体在博弈中寻求最大利益的属性，会使得整个群体在数次迭代后趋向于一个对整体较为有利的情况，使得整个群体得到最大的利益。

参考文献

[1]吴建设, 焦李成, 皎魁,等.基于雪堆博弈进化的复杂网络节点覆盖方法:,CN105050096A[P]. 2015.

程序代码

python代码：

import random

# r<1/kmax
r = 0.1

# 收益矩阵
rewardMat = 
    'C': 'C': (1, 1), 'D': (1 - r, 1 + r),
    'D': 'C': (1 + r, 1 - r), 'D': (0, 0)



# 节点类，每个节点保存节点状态，邻居节点列表和邻居节点个数
class Node:
    def __init__(self):
        if random.random() < 0.5:
            self.state = 'C'
        else:
            self.state = 'D'
        self.value = 0
        self.all_value = 0
        self.neighbour_number = 0
        self.nb = list()


# 博弈网络  迭代更新节点状态，直至收敛
class Net:
    def __init__(self, n):
        self.numbers = n
        self.nodes = list()
        self.edges = list()
        self.reward = 0
        self.initNode()

    # 打印状态
    def printState(self):
        self.getAllReward()
        print('各个节点的决策和其收益：')
        for i in range(self.numbers):
            print('Noede%d:%c ==> reward: %f ' %
                  (i, self.nodes[i].state, self.nodes[i].value))
        print("博弈网络总体回报为:", self.reward)

    # 生成n个结点
    def initNode(self):
        for _ in range(self.numbers):
            tmp_node = Node()
            self.nodes.append(tmp_node)
            print(tmp_node.state)  # 打印初始状态

    # 根据传入的边的列表构建网络
    def buideNet(self, es):
        for e in es:
            self.edges.append(e)
        self.updateNb()

    # 更新每个节点的邻居
    def updateNb(self):
        for a, b in self.edges:
            a.nb.append(self.nodes.index(b))
            b.nb.append(self.nodes.index(a))
        for i in range(self.numbers):
            self.nodes[i].neighbour_number = len(self.nodes[i].nb)

    # 计算每个结点的平均收益,每条边的收益和/边数
    def calValue(self):
        for i in range(self.numbers):
            self.nodes[i].all_value = 0
        for a, b in self.edges:
            a.all_value += rewardMat[a.state][b.state][0]
            b.all_value += rewardMat[a.state][b.state][1]
        for i in range(self.numbers):
            self.nodes[i].value = self.nodes[i].all_value / self.nodes[i].neighbour_number

    # 每次改变一个参与人的策略，增加自己的收益
    # 根据是否有节点发生变化返回是否发生改变的标志
    def updateState(self):
        self.calValue()
        flag = False
        for i in range(self.numbers):
            if self.nodes[i].state == 'C':
                reward1 = self.getReward(i)
                self.nodes[i].state = 'D'
                reward2 = self.getReward(i)
                if reward2 <= reward1:
                    self.nodes[i].state = 'C'
                    continue
                flag = True
            elif self.nodes[i].state == 'D':
                reward1 = self.getReward(i)
                self.nodes[i].state = 'C'
                reward2 = self.getReward(i)
                if reward2 <= reward1:
                    self.nodes[i].state = 'D'
                    continue
                flag = True
        return flag

    # 计算单个结点的收益，某节点的所有边的收益/邻居个数
    def getReward(self, i):
        all_value = 0
        for s in self.nodes[i].nb:
            all_value += rewardMat[self.nodes[i].state][self.nodes[s].state][0]
        value = all_value / self.nodes[i].neighbour_number
        return value

    # 获得博弈网络的总收益
    def getAllReward(self):
        for a, b in self.edges:
            self.reward += sum(rewardMat[a.state][b.state])
        return self.reward


if __name__ == '__main__':
    net = Net(15)
    # 博弈网络中边的集合
    edge_list = [(0, 1), (0, 2), (0, 6), (0, 7),
                 (1, 2), (1, 4), (1, 9),
                 (2, 8), (2, 10), (2, 11),
                 (3, 5), (3, 12),
                 (4, 14),
                 (5, 13),
                 (6, 11), (6, 14),
                 (8, 9),
                 (12, 14)
                 ]

    net.buideNet((net.nodes[a], net.nodes[b] for a, b in edge_list))

    # 循环更新节点状态，直至每个人都不愿改变自己的决策
    while net.updateState():
        net.printState()  # 打印中间状态
    net.printState()