课程笔记人工智能导论——从四个学校东拼西凑的产物
Posted lokol.
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了课程笔记人工智能导论——从四个学校东拼西凑的产物相关的知识,希望对你有一定的参考价值。
本笔记参照西安电子科技大学、浙江工业大学、哈尔滨工业大学慕课以及北京交通大学课程PPT记录。
如有错误,敬请指正!
第三章
一阶谓词逻辑表示法
谓词
谓词包括一元谓词、二元谓词、多元谓词
- 个体是常量:一个或者一组指定的个体;
- 个体也可以是变量:没有制定的一个或者一组个体;
- 变量具体赋值后,才能确定真假
- 个体可以是函数:一个个体到另一个个体的映射;
- 个体可以是谓词。
谓词公式:
单个谓词是谓词公式,称为原子谓词公式。
谓词公式的性质:
- 永真性

- 可满足性

- 等价性
- 永真蕴含
连接词
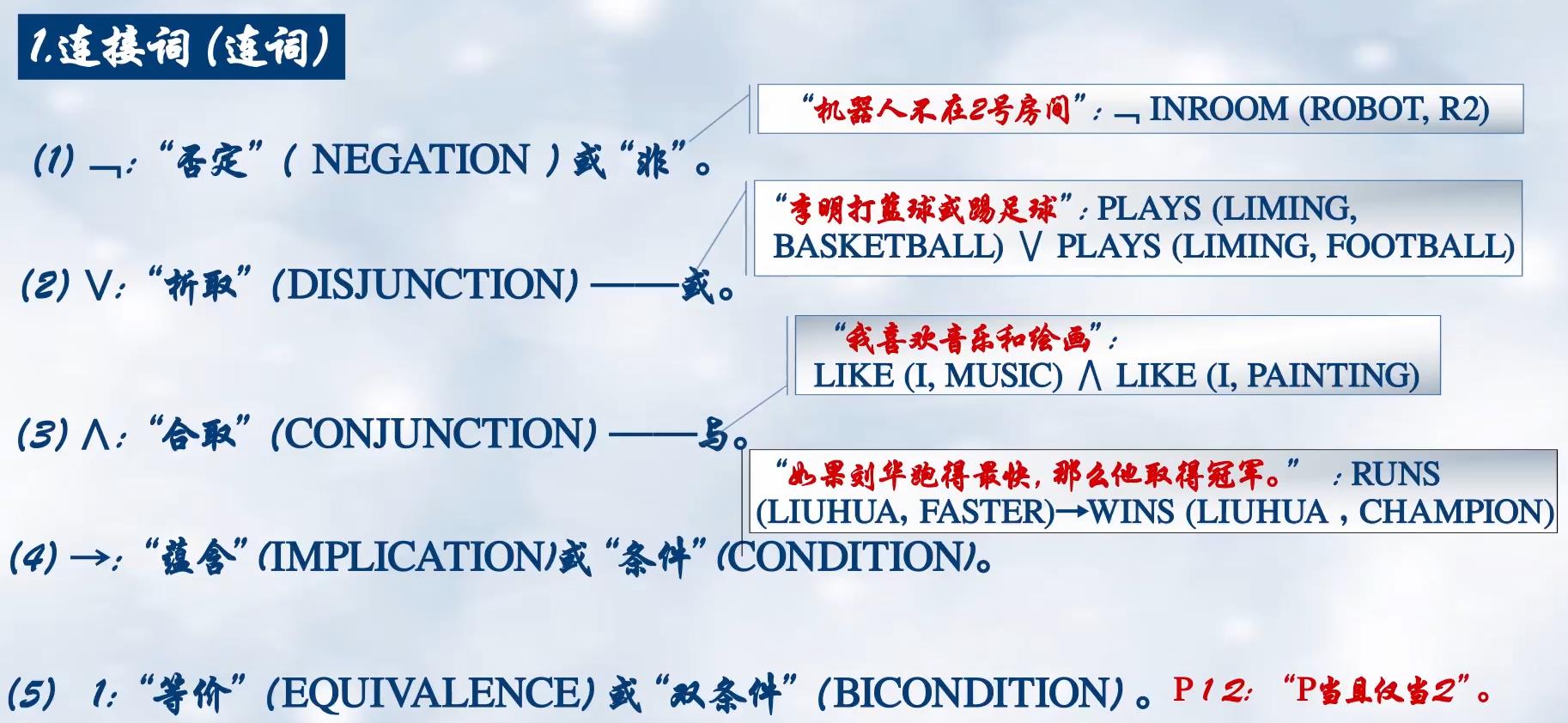
蕴含关系:P→Q,仅当Q为F时,表达式才为假
量词
- 全称量词
- 存在量词
全称量词和存在量词在同一命题中的次序会影响命题意思。
量词辖域:
量词辖域:位于量词后面的单个谓词或者用括弧括起来的谓词公式。
约束变元与自由变元:辖域内与量词中间名的变元称为约束变元,不同名的变元称为自由变元。
一阶谓词逻辑知识表示法
步骤:
- 定义谓词及个体
- 变元赋值
- 用连接词连接各个谓词,形成谓词公式
特点:
- 优点
- 自然性
- 精确性
- 严密性
- 容易实现
- 缺点
- 不能表示不确定的知识
- 组合爆炸
- 效率低
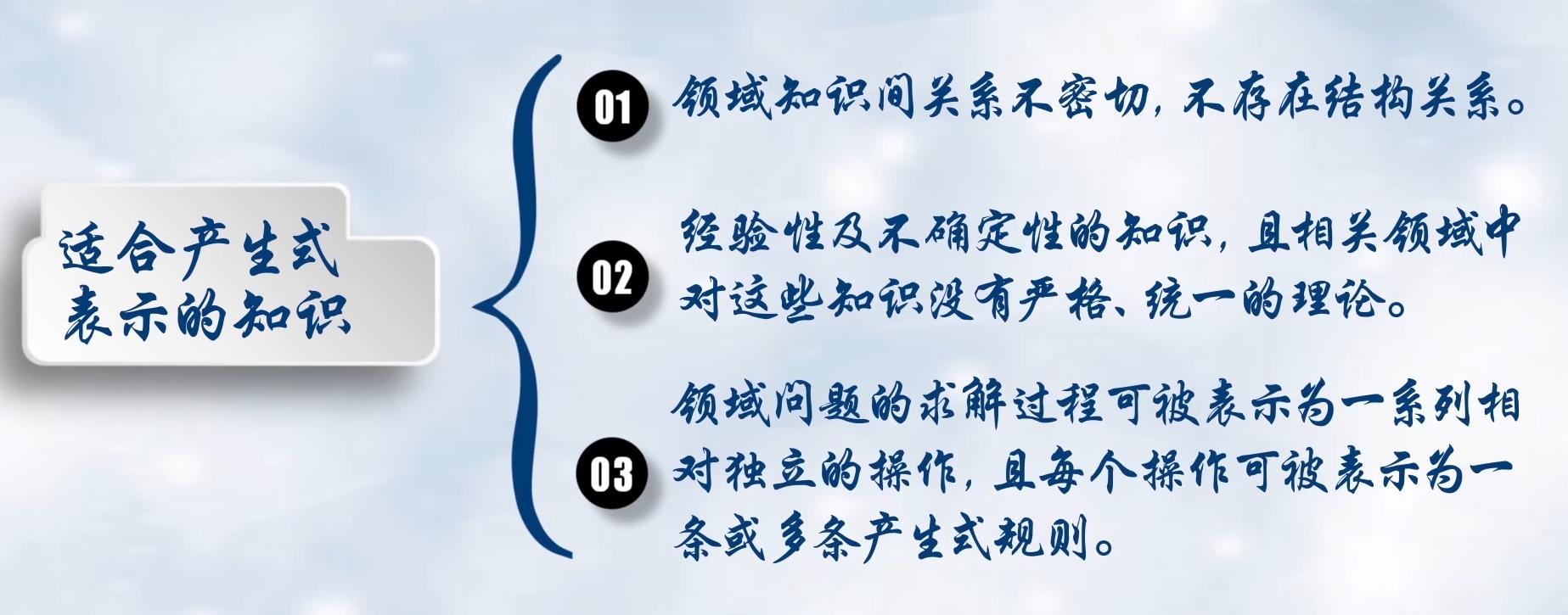
产生式规则表示法
确定性规则:
只要前提满足,结论一定正确
基本形式:IF P THEN Q、 或 P→Q、
不确定性规则:
基本形式:IF P THEN Q(置信度) 或 P→Q(置信度)
确定性事实性知识:
表示:(对象,属性,值) 或 (关系,对象1,对象2)
不确定性事实性知识:
表示:(对象,属性,值,置信度) 或 (关系,对象1,对象2,置信度)
产生式与蕴含式的区别:
- 除逻辑蕴含外,产生式还包括各种操作、规则、变换、算子、函数等。
- 蕴含式只能表示精确知识,产生式还可以表示不精确的知识。
巴科斯范式BNF(backus normal form):

产生式系统
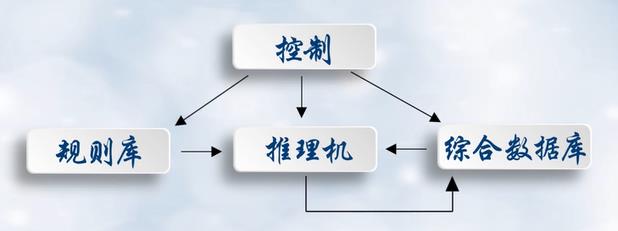
- 规则库:相应领域内知识的产生式集合
- 综合数据库:存放问题求解过程中各种当前信息的数据结构
- 控制系统:由一组程序组成,负责整个产生式系统的运行,实现对问题的求解
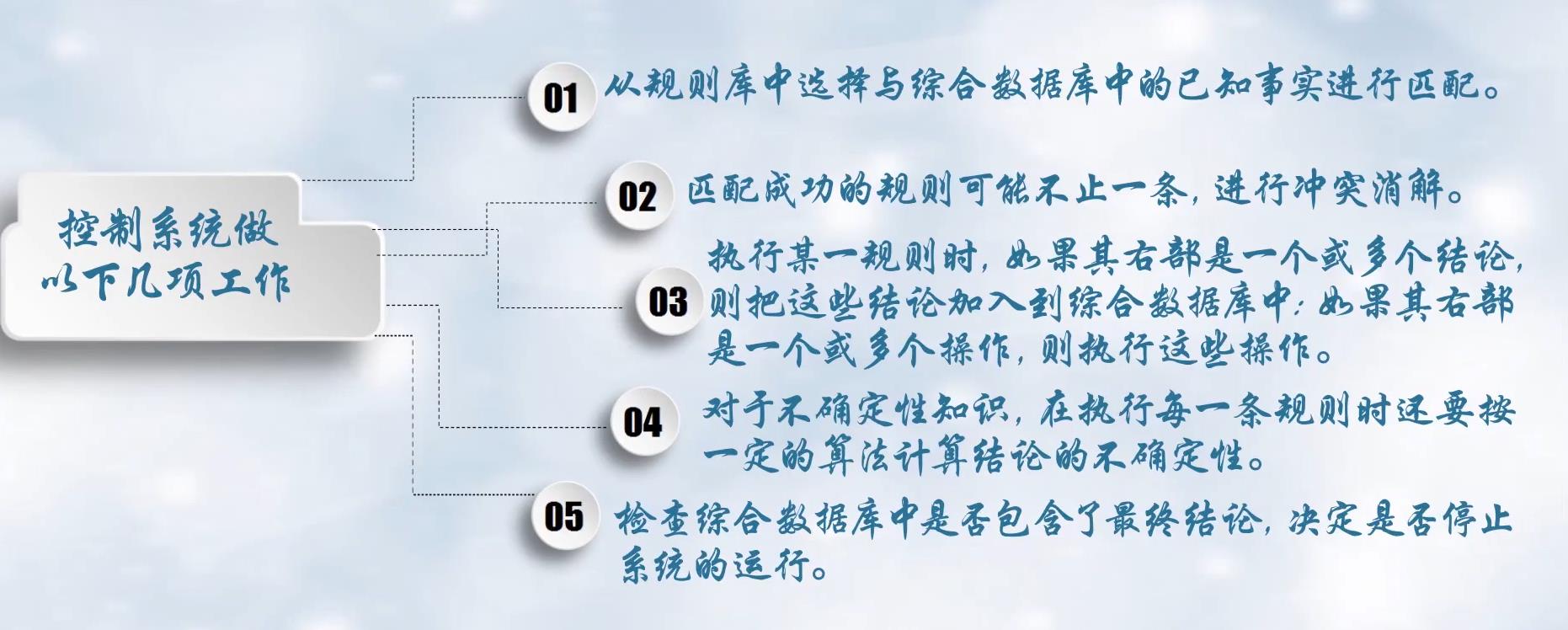
产生式系统就是不断对特征进行匹配,并将匹配结果加入特征中,知道匹配到相应结果。
语义网络表示法

两个弧连接的结点之间的关系默认为合取关系。用封闭的虚线作为析取界限,表示析取关系,并注以DIS。
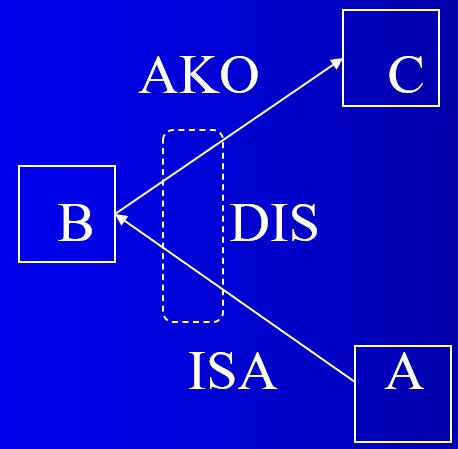
如果合取关系嵌套在析取关系内部,也应用虚线围起来,并标以CONJ。
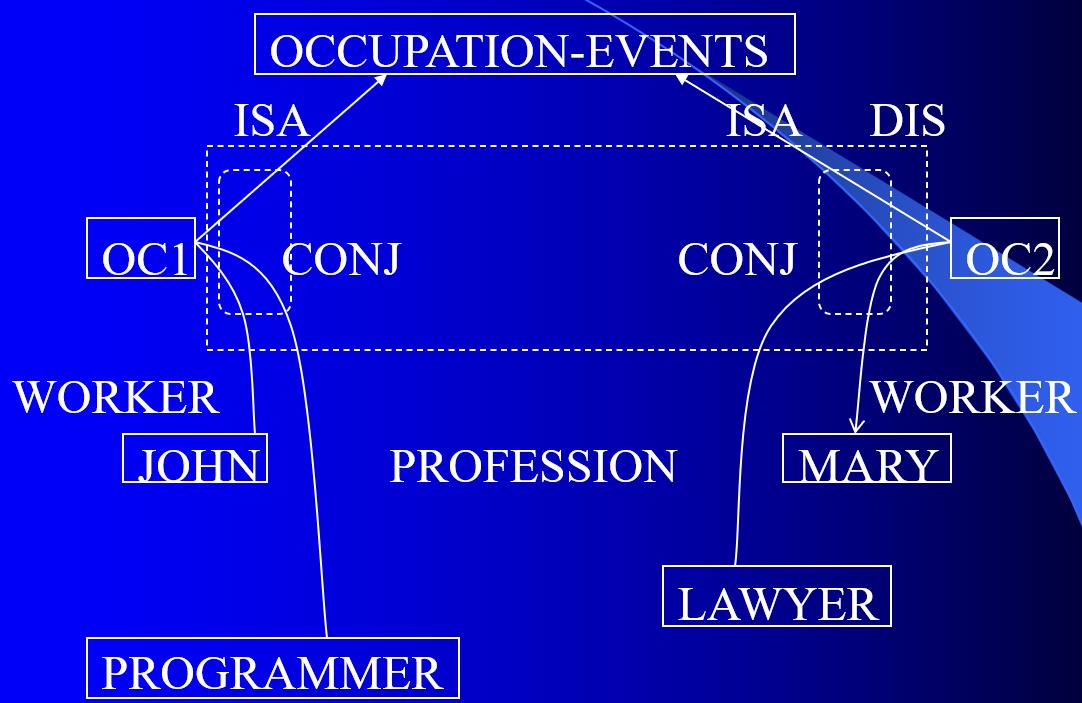
“非”的关系用NEG表示。

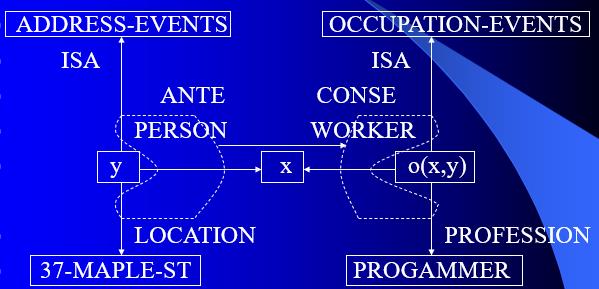
蕴涵关系用一对封闭虚线表示,前项标以ANTE,后项标以CONSE。
具有继承性的关系:
- ISA:表示层次关系
- AKO:表示集合关系
- ISPART:表示组成关系
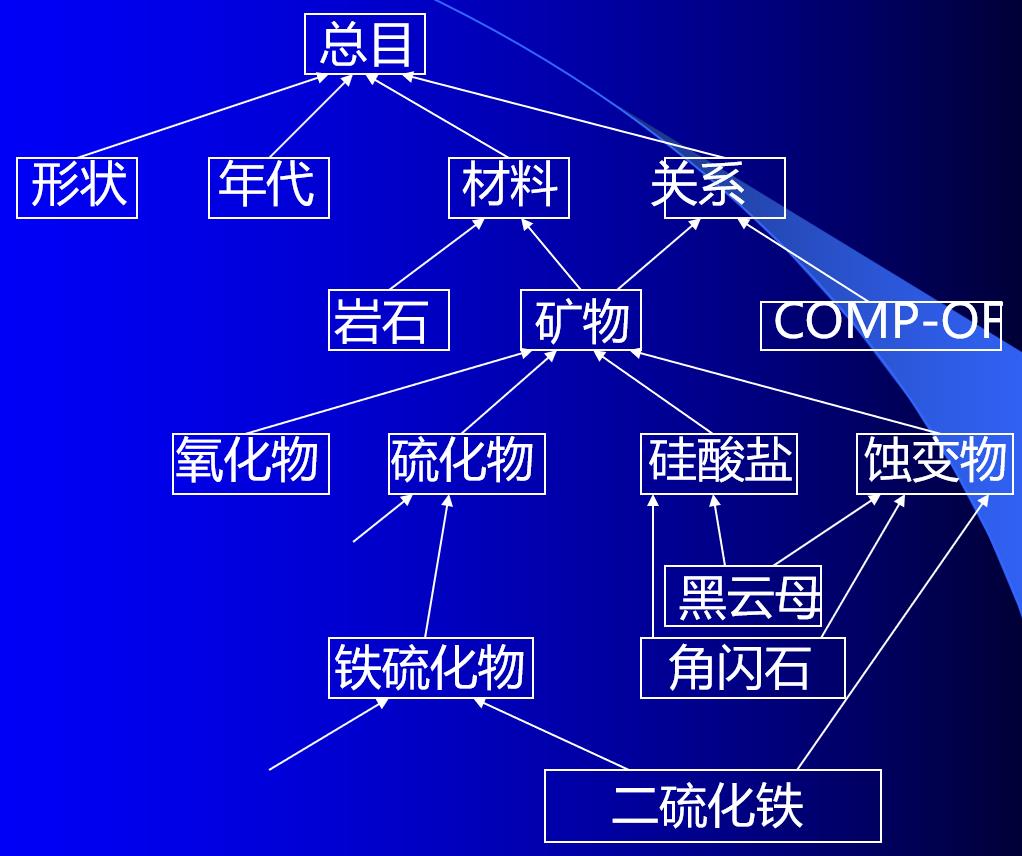
分块语义网络
结点:物理实体、概念、性质和关系。
弧:该关系所涉及参数。
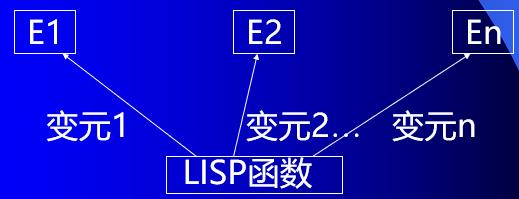
lFORM-OF、COMP-OF均为LISP函数,在语义网络中表示为:

分类学网络
推理网络
点:断言,取值为真、假,或附以确信度。
弧:规则。
结点格式:

规则格式:

推理方式——混合主动式:
过程:不断修改各结点的可信度(后验概率),直至顶层结点的可信度超过某一阈值为止。
- 正向推理:每当用户输入一个证据E及其可信度,系统就沿推理网络修改各结点的可信度。
- 主动式推理:在推理的任何时刻,用户都可以为系统提供信息(任何层次结点的信息)。
- 反向推理:正向推理结束后,如果已经确定了存在某种矿藏,则输出结果;否则进行反向推理,为断定某种矿藏的成矿寻找有关数据。
框架表示法
一种描述所论对象属性的数据结构。

框架结构

例:教师框架

框架表示法的特点
- 结构性:便于表达结构性知识,能够将知识的内部结构关系及知识间的联系表示出来
- 继承性:框架网络中,下层框架可以继承上层框架的槽值,也可以进行补充、修改
第四章
问题规模很大或很复杂,以至于不可能考虑其目标的全部可能性时,以解决寻优问题为目标的优化算法就转变为局部搜索。
局部搜索算法的终止条件一般有两种选择:
- 时间限制
- 搜索获得的当前目标不能再改善
状态空间表示法
状态空间法:基于解答空间的问题表示和求解方法,它是以状态和算符为基础来表示和求解问题的。
主要包括:状态、算符、状态空间
状态
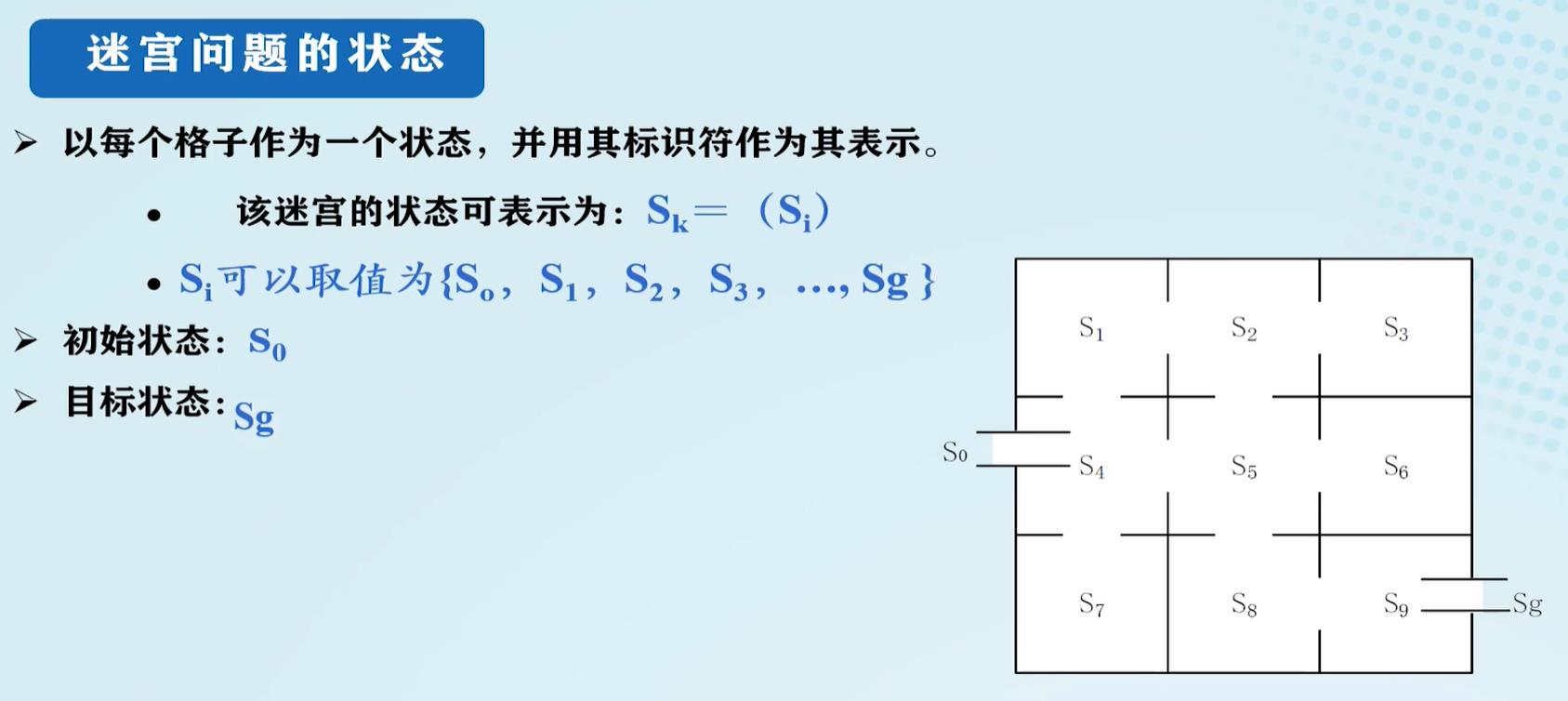
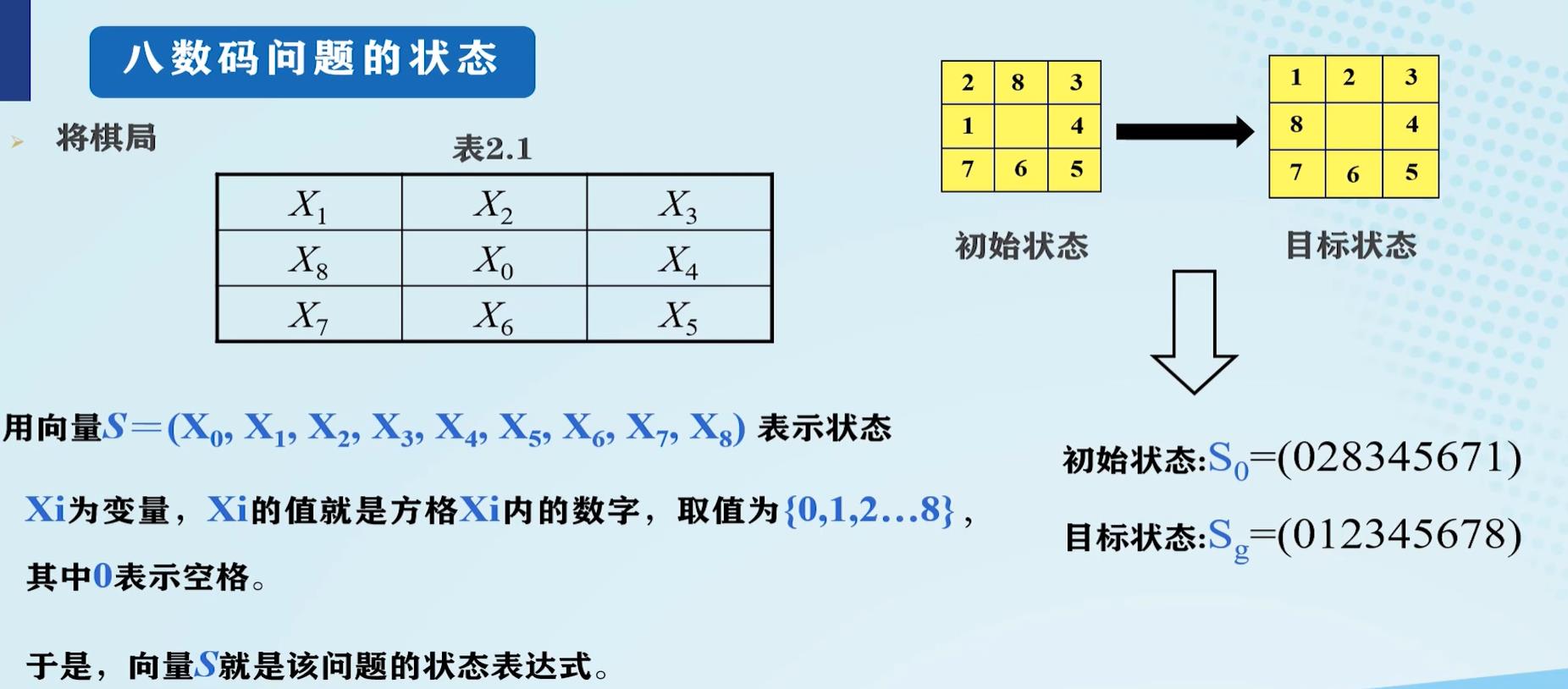
状态:表示问题求解过程中每一步问题状态的数据结构,一般用一组数据表示:
S
k
=
{
S
k
0
,
S
k
1
,
.
.
.
}
S_k=\\{Sk_0, Sk_1, ...\\}
Sk={Sk0,Sk1,...}
式中每个元素为集合的分量,称为状态变量。
迷宫问题的状态表示:
八数码问题的状态表示:
算符
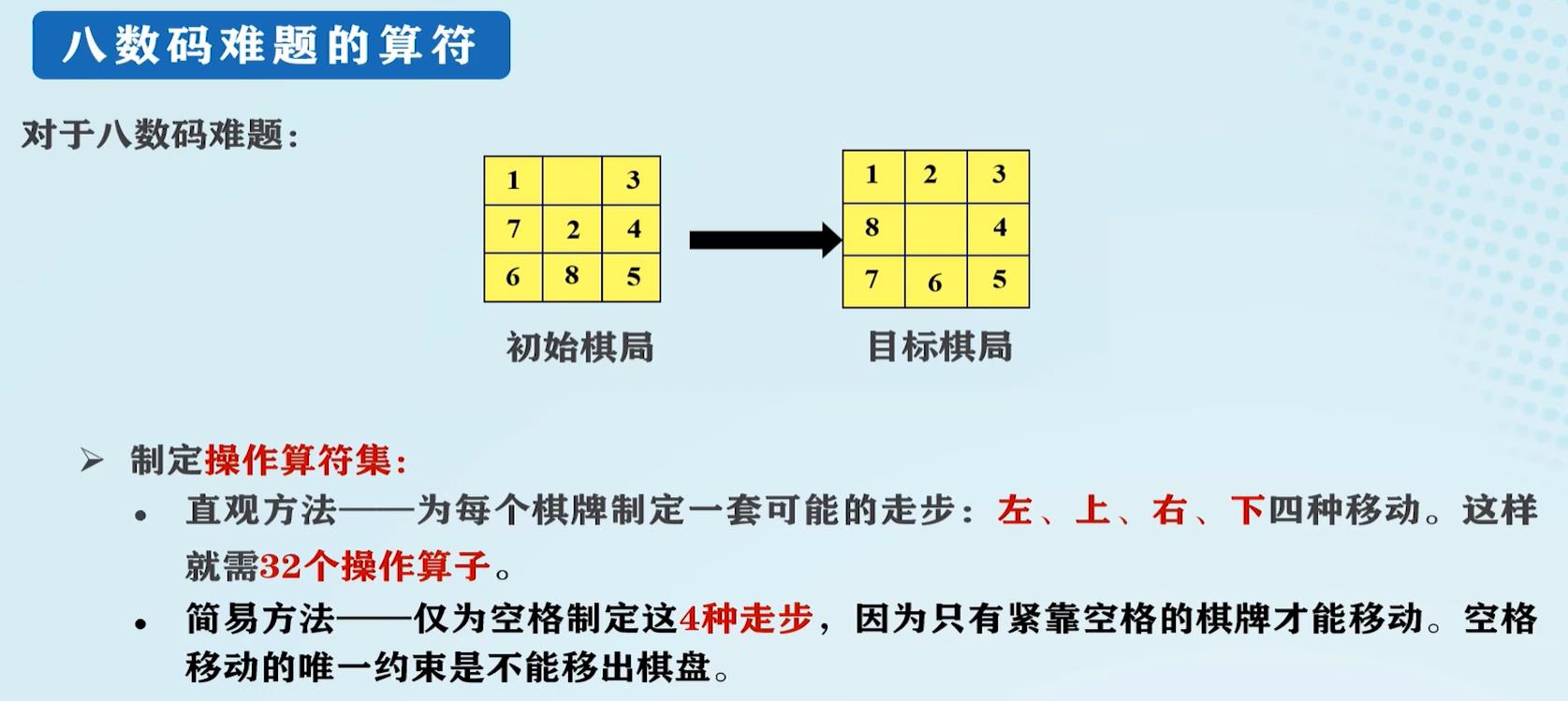
算符:当对一个问题状态使用某个可用操作时,它将引起该状态中某些分量值的变化,从而使问题从一个具体状态变为另一个具体状态。

迷宫问题的算符:

八数码难题的算符:
问题的状态空间
问题的状态空间:用来描述一个问题的全部状态以及这些状态之间的互相关系。
状态空间常用一个三元组表示: ( S , F , G ) (S, F, G) (S,F,G)。
- S S S:为问题的所有初始状态的集合;
- F F F:算符的集合;
- G G G:为目标状态的集合。

八数码的状态空间:
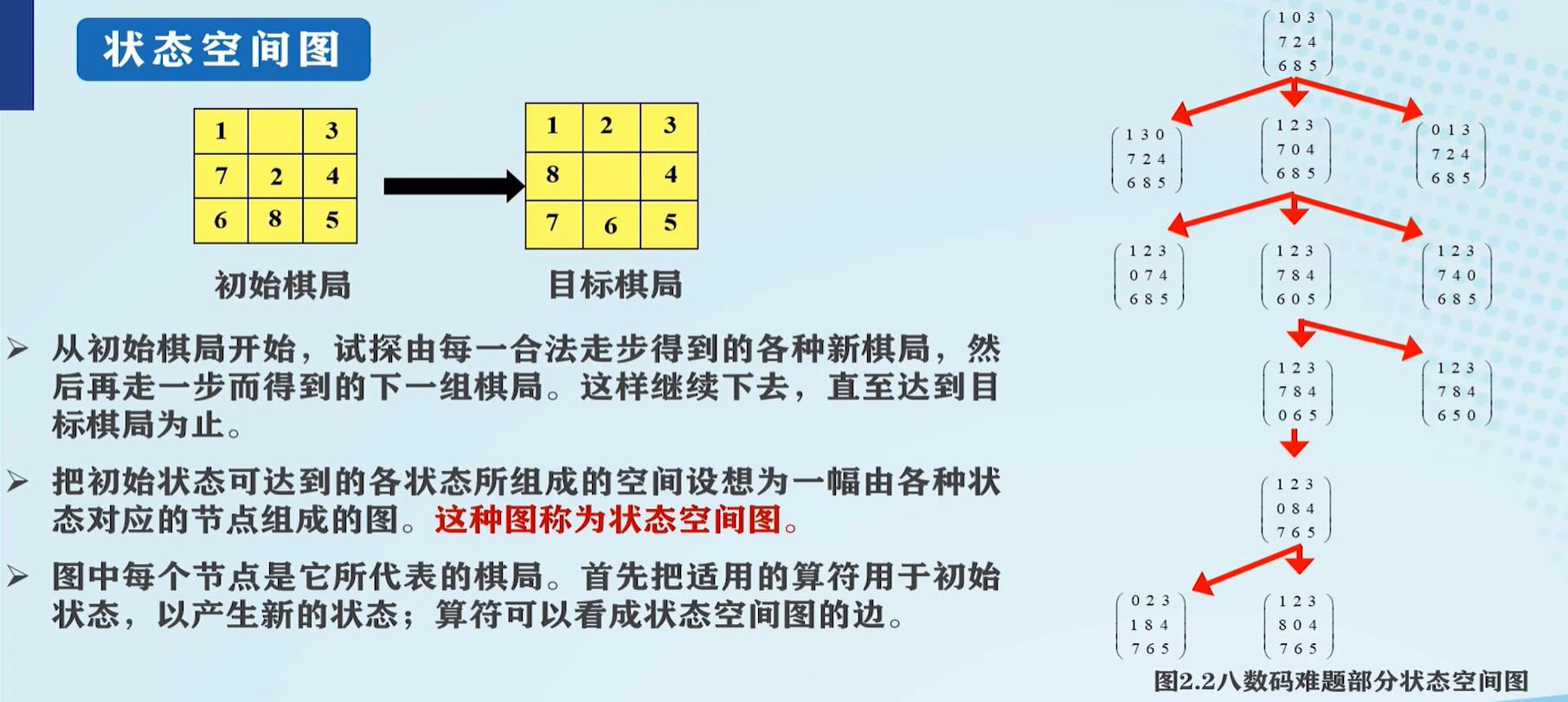
状态图示法:状态空间的图示形式,其中节点表示状态,边表示算符,求解过程就是求相应路径的问题(搜索)。
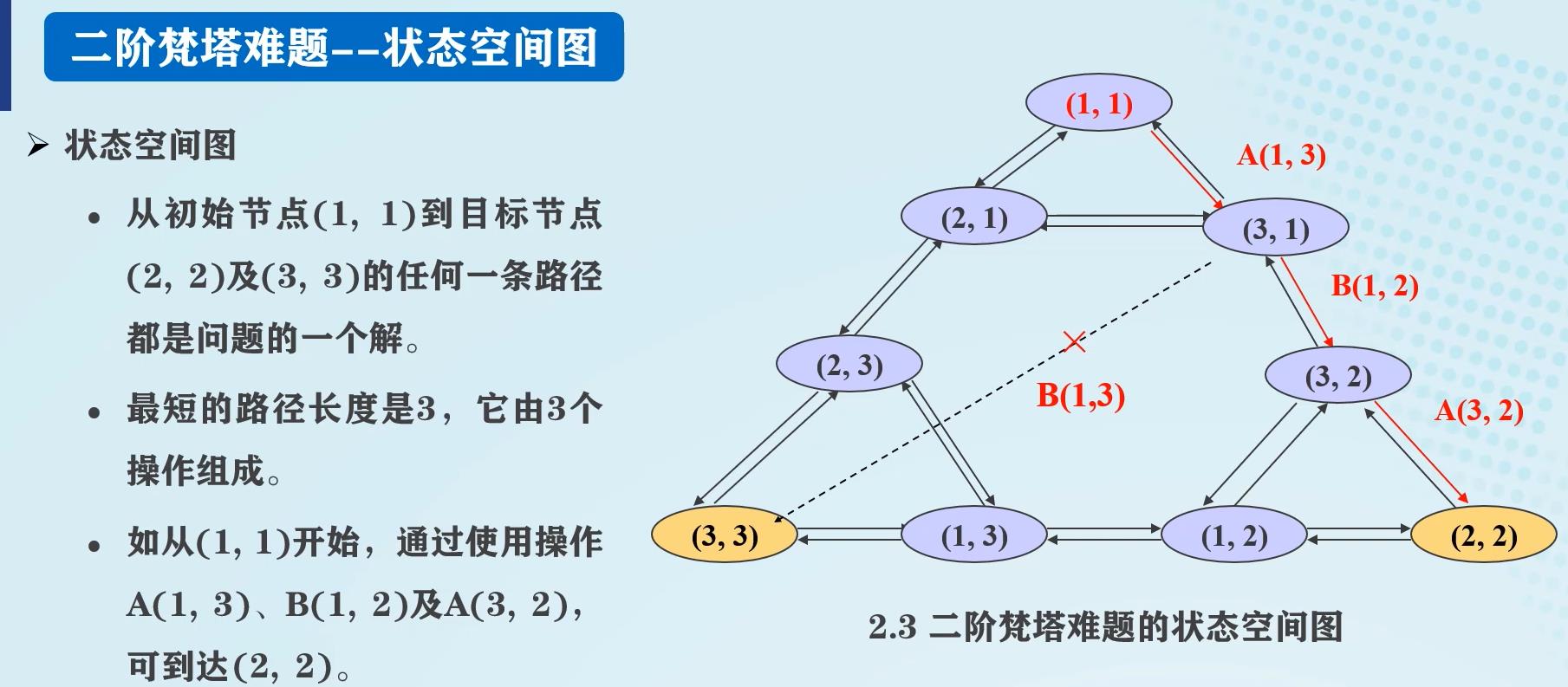
二阶梵塔难题
状态:

算符:

状态空间图:
爬山法

局部最大值可能出现在局部最大值、“平坦”局部最大值、山肩的平坦处。
爬山法是一种贪心算法,即从当前状态出发,向相邻状态进行试探,若发现某个相邻转台比当前状态更好,则转入相邻状态并放弃当前状态。

八皇后问题
八皇后问题若不做任何约束,则可能的排列数很大。若限制每个皇后只能再同一行或同一列移动,则排列数大大减少。
八皇后问题中,需要采用一个代价函数h。其代表再八皇后问题中,两两冲突对的个数h值不能增加,只能慢慢减少,以此作为标准判断是否从当前状态移动到相邻状态。
图搜索问题
图的概念
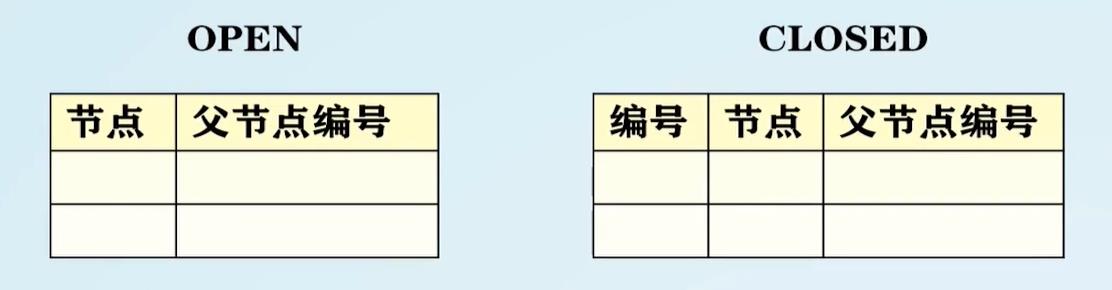
- OPEN表:记录带拓展节点
- CLOSED表:记录已拓展的节点
- 必须记住从目标返回的路径
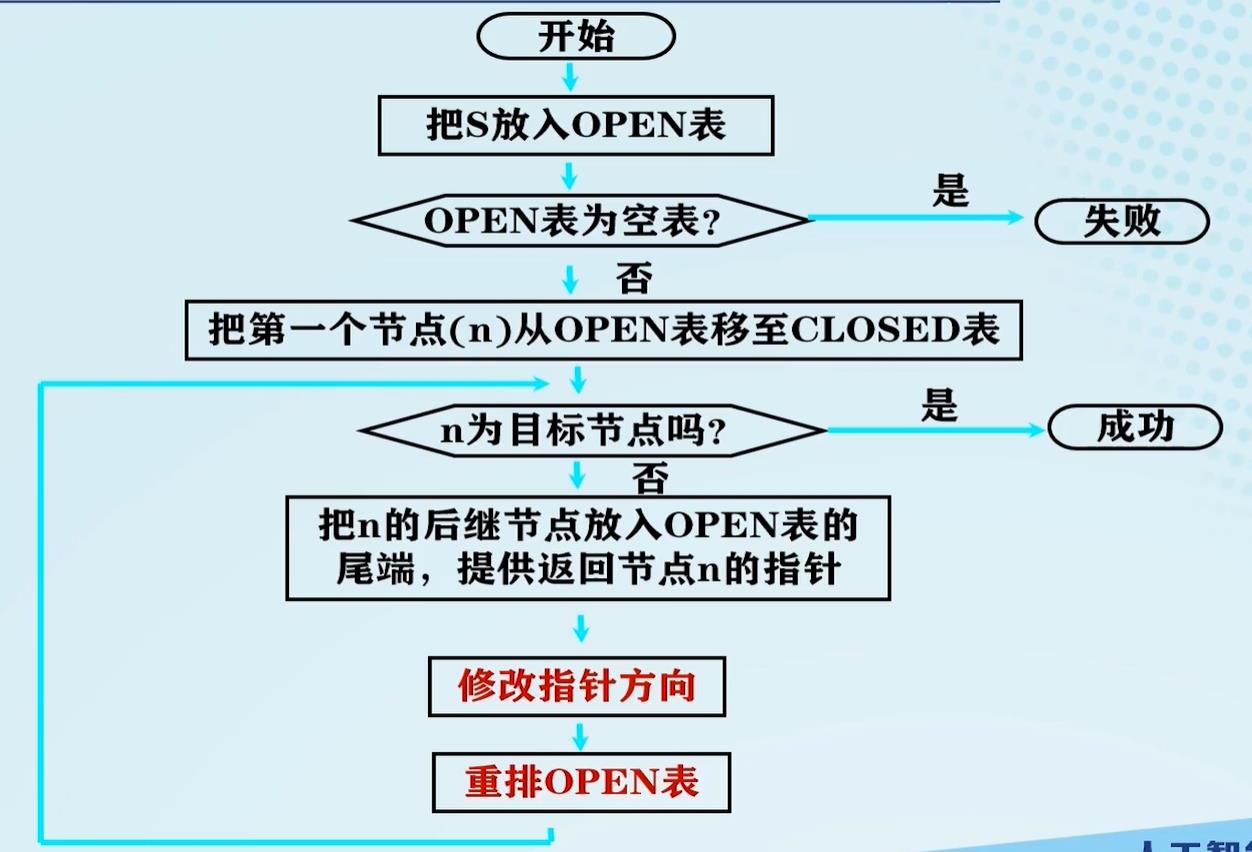
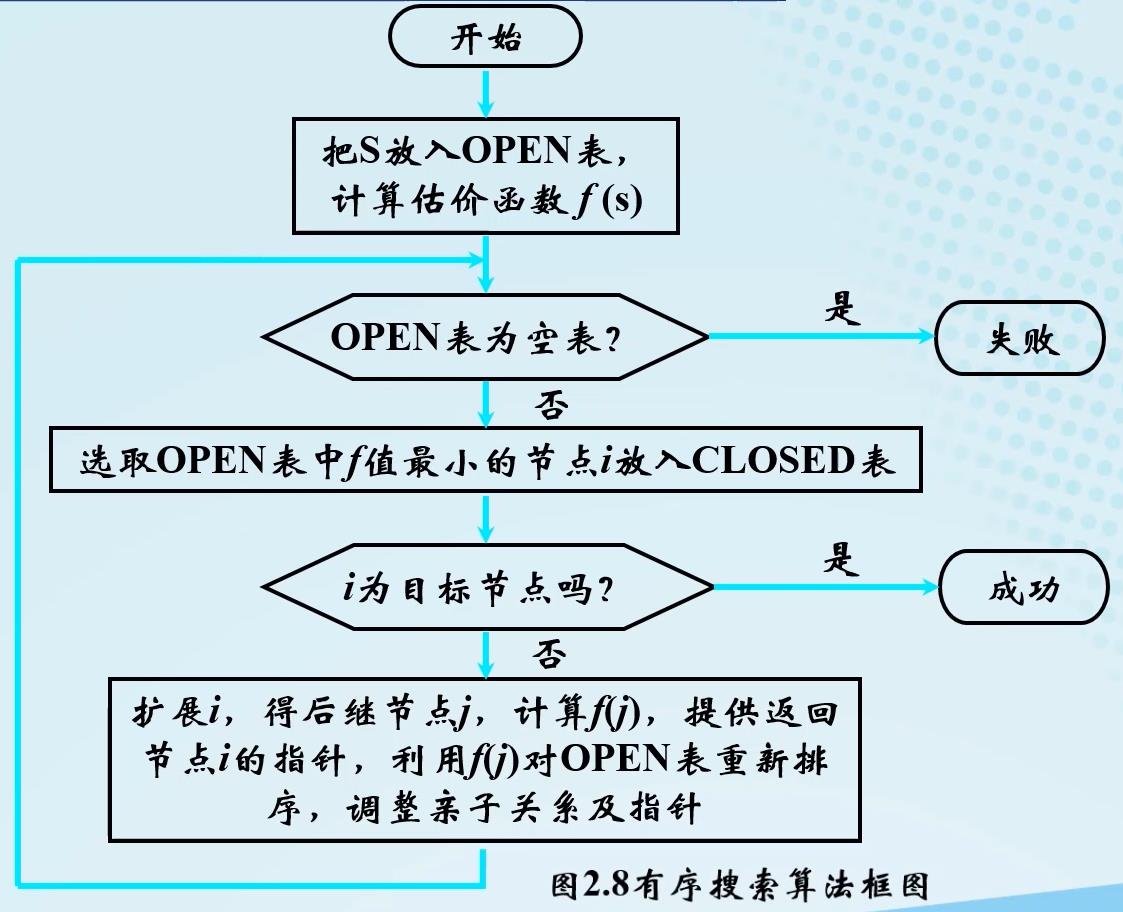
图搜索流程:
搜索图:算法结束后,所生成的“足迹”为一个图 G G G。
搜索树:由于每个节点都有一个指针指向父节点,这些指针指向的节点构成 G G G的一个支撑树。
图搜索分类
对OPEN表中节点排序方式产生了不同的搜索策略,不同的搜索搜索策略效率不同。
- 无信息搜索(盲目式搜索)
- 宽度优先搜索
- 深度优先搜索
- 等代价搜索
- 有信息搜索(启发式搜索)
- A算法
- A*算法
盲目式搜索
按预定的控制策略进行搜索,在搜索过程中获得的中间信息不用来改进控制策略。
宽度优先搜索(BFS):
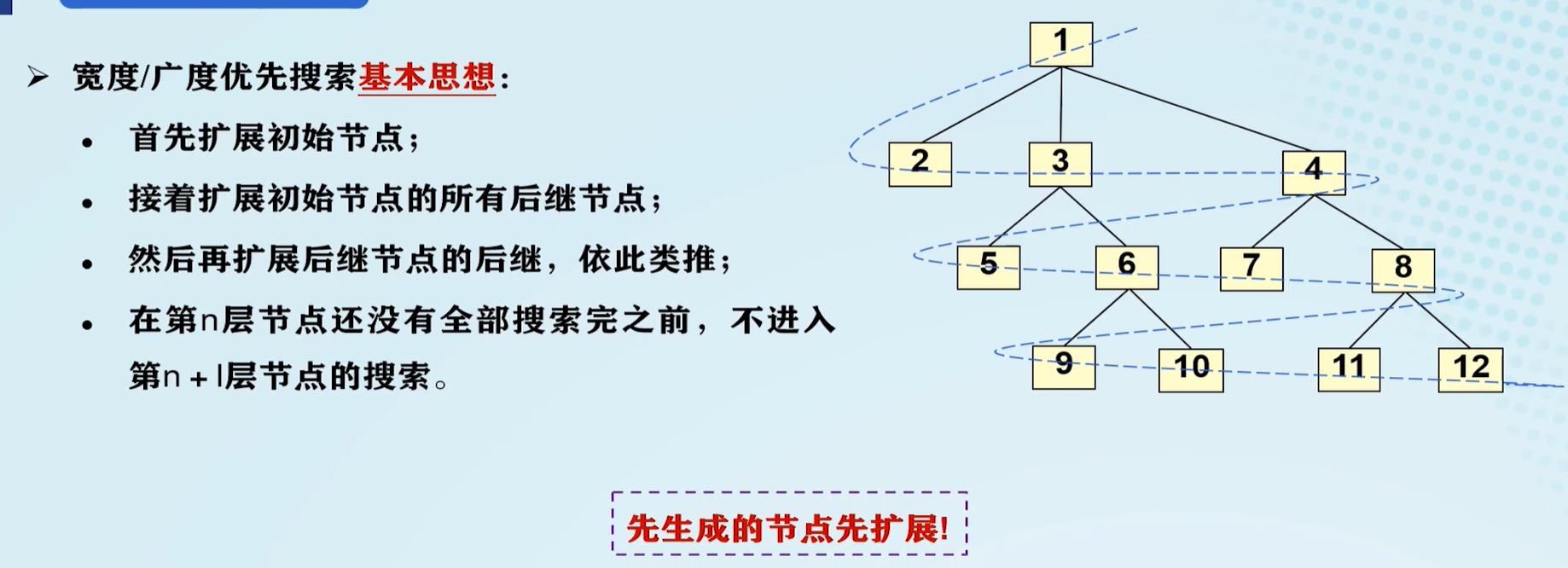
BFS的性质:
- 属于图搜索
- 新拓展的节点排在OPEN表末端
- 当问题有解时,一定能找到解
- 方法与问题无关,具有通用性
- 效率较低
深度优先搜索(DFS):
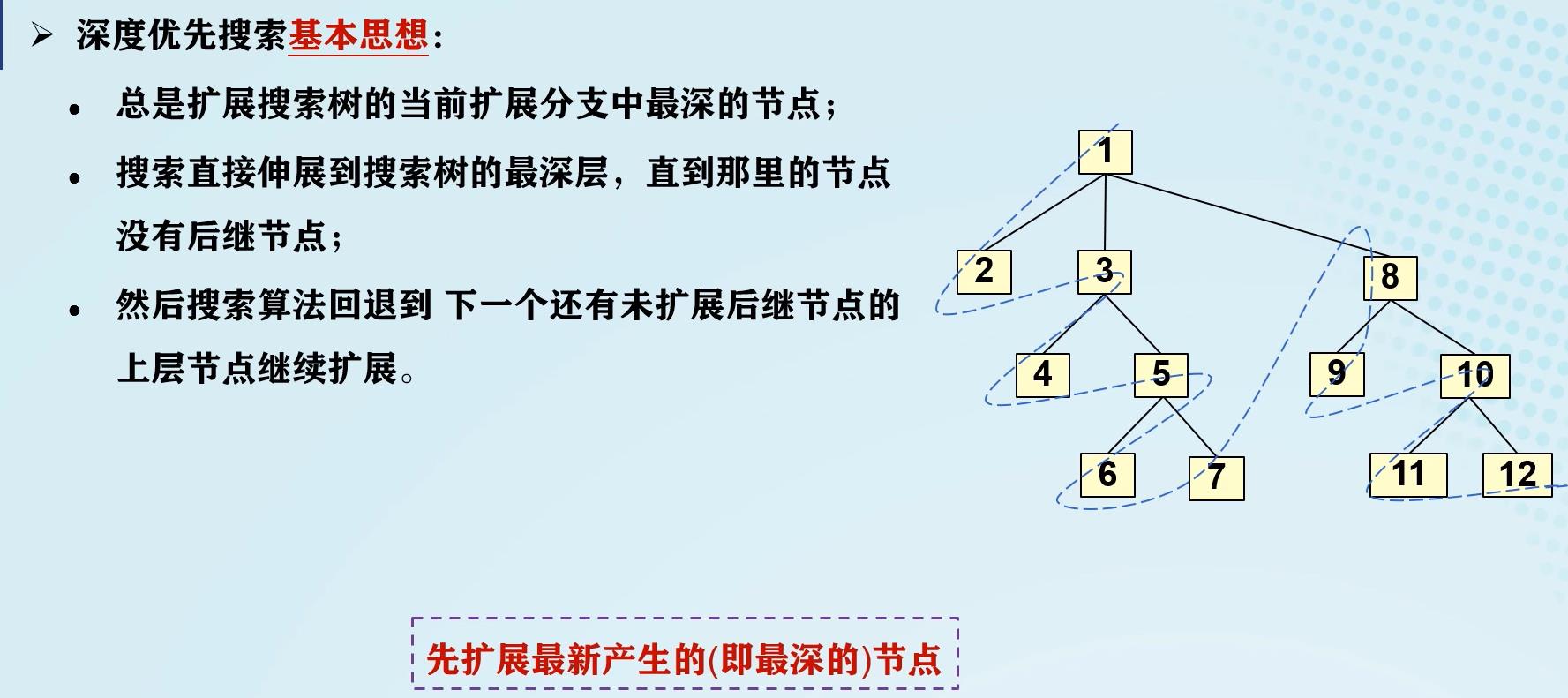
与BFS的不同在于,DFS将待拓展的节点放在OPEN表的开头。
节点深度:
- 起始节点深度为0。
- 任何其他节点的深度为其父辈节点深度加1。
DFS的特点:
- 搜索一般不能找到最优解。若解在该分支上,则能很快找到解;若解不在该分支上,则不能;若该分支为无穷深度,则永远不可能找到解。可以定义深度界限 d m d_m dm来解决这个问题。
- 深度界限 d m d_m dm 不合理时,也有可能找不到解,如 d m d_m dm定义过小的情况。将 d m d_m dm更改为可变深度限制可以在一定程度上解决这个问题。
等代价搜索:

核心思想:利用边的代价,对OPEN表进行排序。若每条边的代价为1,则等代价搜索即为BFS。
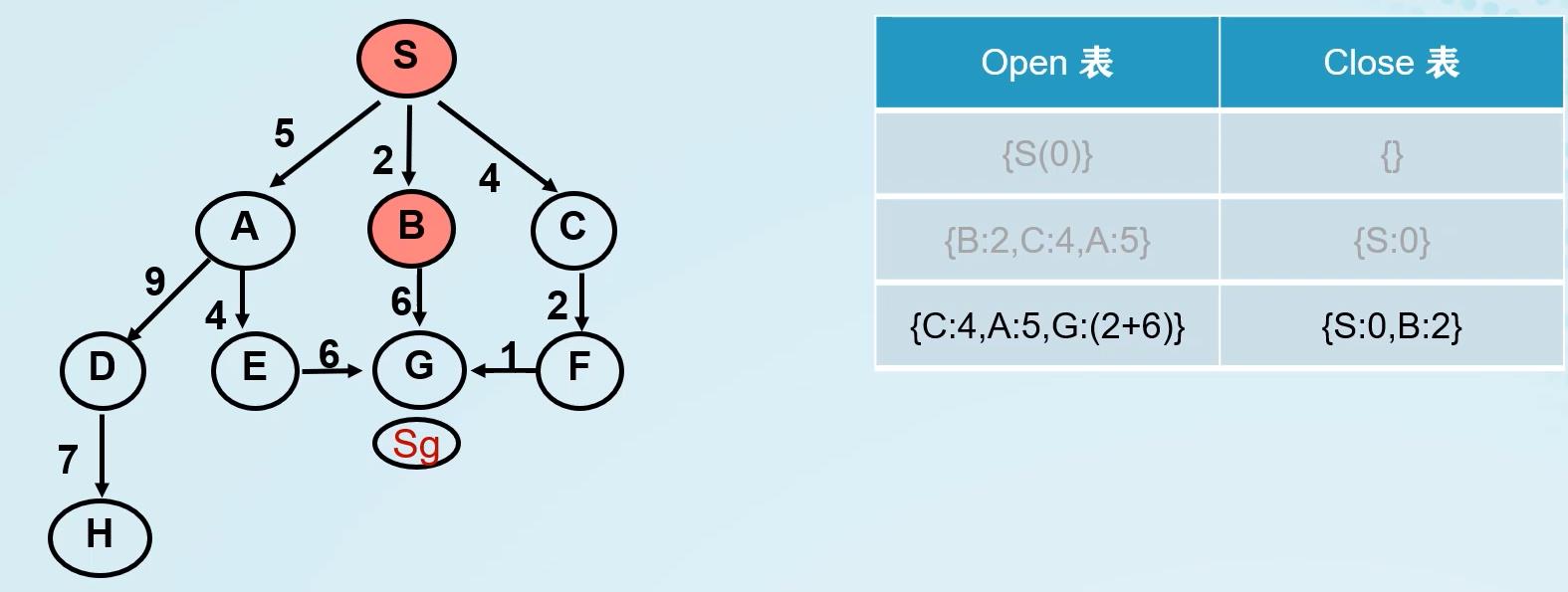
小结:
- BFS按“层”进行搜索,先进入OPEN表的节点先被考察。
- DFS沿纵深方向进行搜索,后进入OPEN表的节点先被考察。
- 等代价搜索首先扩展最小代价节点。
启发式搜索
盲目式搜索的缺点:效率低,耗费过多的计算空间与时间。
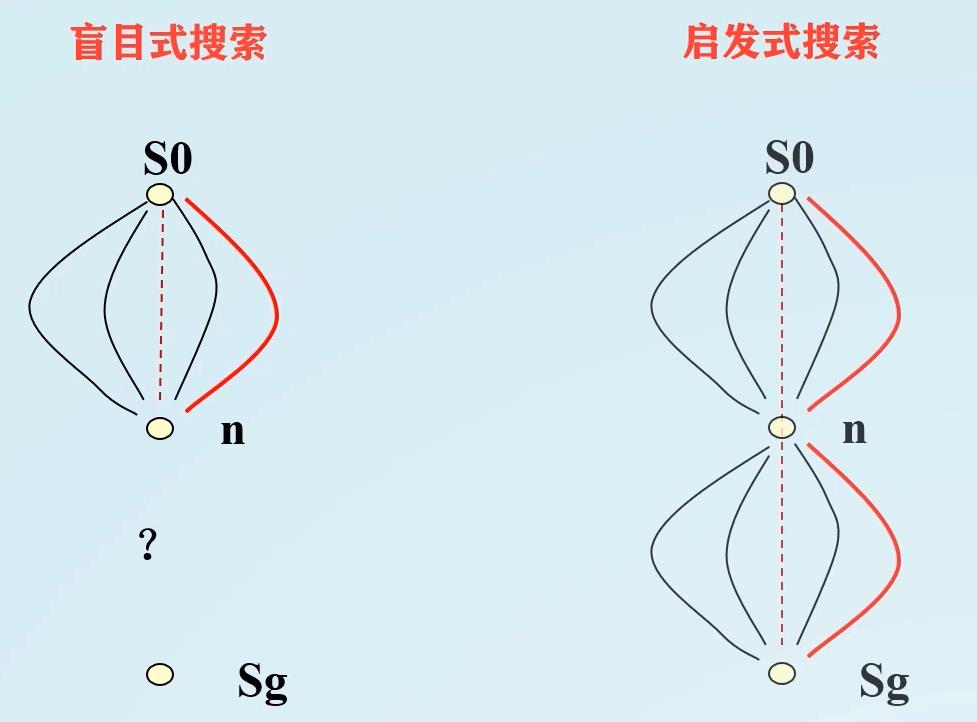
盲目式搜索只知道 S 0 → n S_0→n S0→n,但是启发式搜索可以通过 S 0 → n S_0→n S0→n及 n → S g n→S_g n→Sg两者来判断目标,向最有希望的方向搜索。
八数码难题:
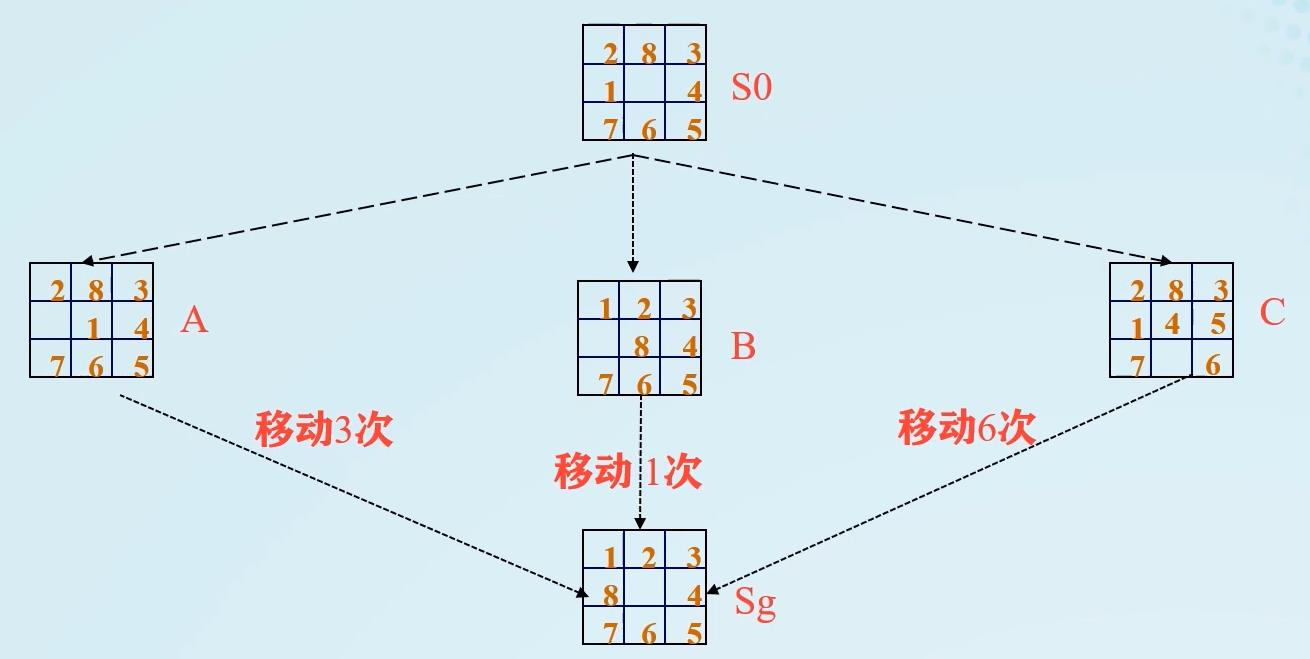
S 0 S_0 S0与 S A S_A SA、 S B S_B SB、 S C S_C SC相比, S B S_B SB与 S g S_g Sg最相似,变为 S g S_g Sg移动次数最少,故先拓展 B B B节点。
启发式信息:与具体问题求解过程有关的,并可知道搜索过程朝着最有希望的方向前进的控制信息。
启发式需要猜测:
- 从节点 n n n开始,找到最优解的可能性?
- 从起始节点开始,经过节点 n n n,到达目标节点的最佳路径的费用?
要解决这些问题,需要定义一个评价函数
f
(
n
)
f(n)
f(n),用于估算节点“希望”程度。
f
(
n
)
=
g
(
n
)
+
h
(
n
)
f(n)=g(n)+h(n)
f(n)=g(n)+h(n)
g
(
n
)
g(n)
g(n):从起始状态到当前状态
n
n
n的代价。
h ( n ) h(n) h(n):从当前状态到目标状态的估计代价(启发函数)。
A算法:
-
局部择优算法
- 把初始节点 S 0 S_0 S0放入OPEN表中,表示 f ( S 0 ) f(S_0) f(S0);
- 如果OPEN表为空,则问题无解,退出;
- 把OPEN表的第一个节点(记为节点 n n n),放入CLOSED表中;
- 考察节点 n n n是否为目标节点,若是,则得解,退出;
- 若节点 n n n不可拓展,则转第2步;
- 拓展节点 n n n,用评价函数 f ( x ) f(x) f(x)计算每个子节点,并按评价值从小到大的顺序依次放入OPEN表的首部,并为每一个子节点都配置指向父节点的指针,转第2步。
-
有序搜索算法:选择OPEN表中具有最小 f f f值的节点作为下一个要拓展的节点。
八数码难题难题的有序搜索搜索图:
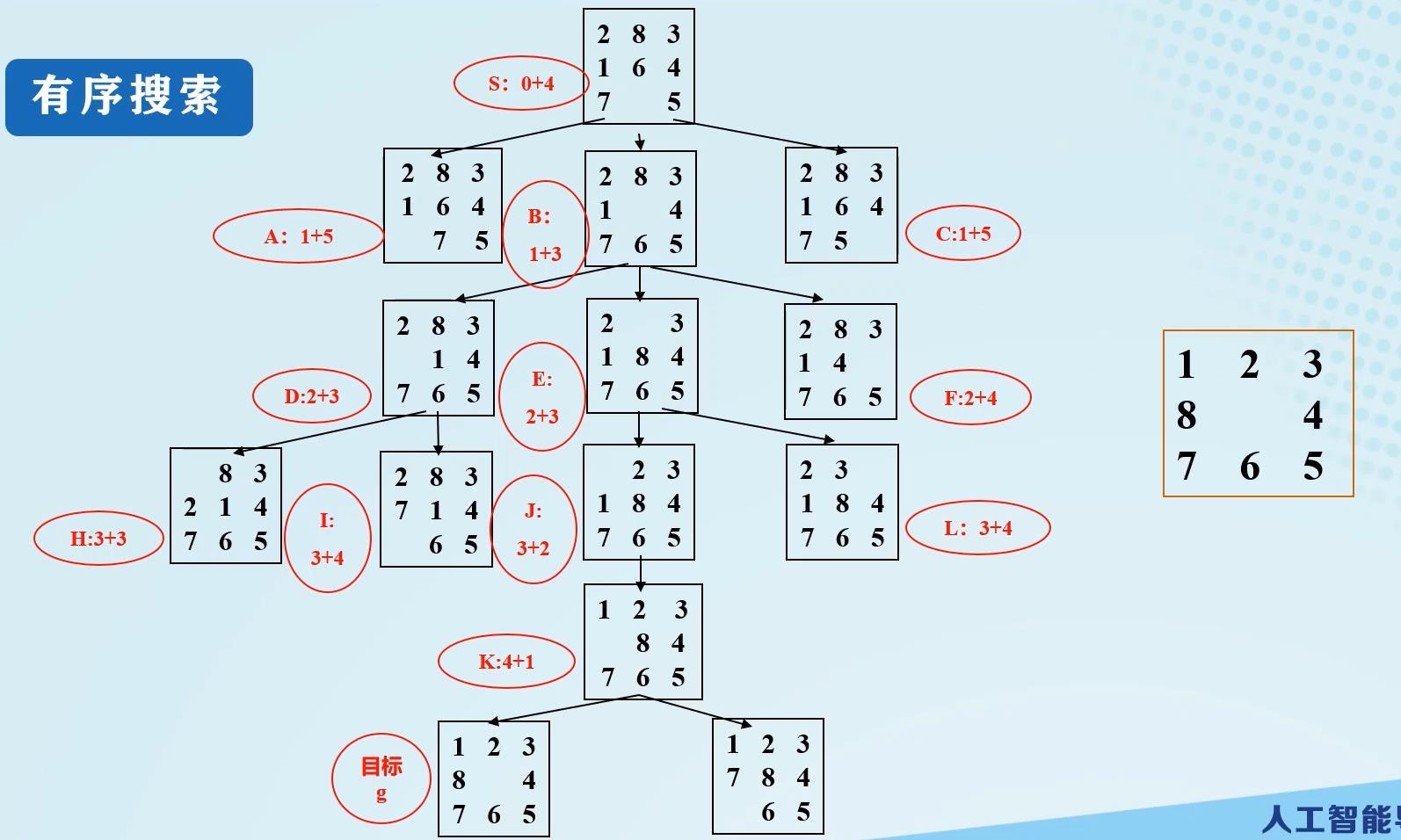
有序搜索有一点儿类似DFS。
A*算法:
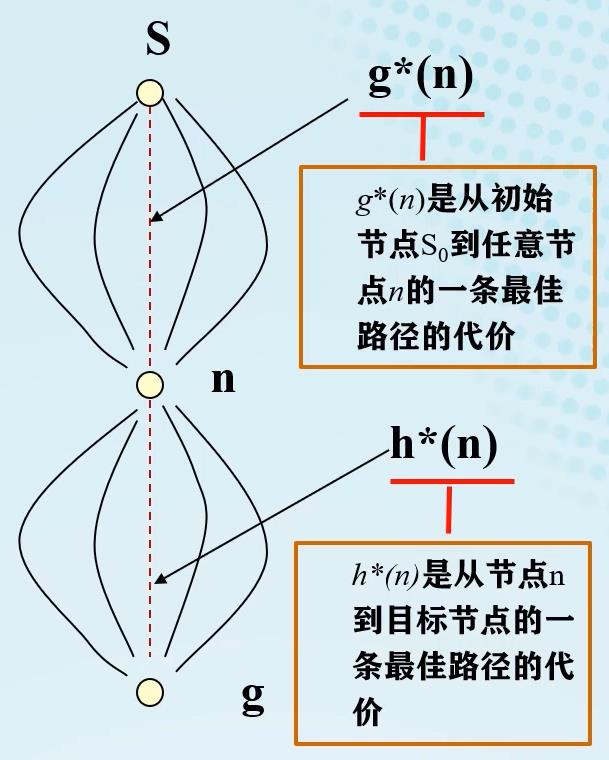
g ∗ ( n ) g^*(n) g∗(n):从初始节点 S 0 S_0 S0到任意节点 n n n的一条最佳路径的代价。
h ∗ ( n ) h^*(n) h∗(n):从节点 n n n到目标节点的一条最佳路径的代价。
A*算法有评价函数:
f
(
n
)
=
g
(
n
)
+
h
(
n
)
f(n)=g(n)+h(n)
f(n)=g(n)+h(n)
- g ( n ) g(n) g(n)是对 g ∗ ( n ) g^*(n) g∗(n)的估计, g ( n ) > = g ∗ ( n ) g(n)>=g^*(n) g(n)>=g∗(n)
-
h
(
n
)
h(n)
h(n)是对
h
∗
(
n
)
h^*(n)
h∗(n)的估计,且满足对所有的
n
n
n,
h
(
n
)
⩽
h
∗
(
以上是关于课程笔记人工智能导论——从四个学校东拼西凑的产物的主要内容,如果未能解决你的问题,请参考以下文章