怎么理解分位数

Posted 2023-04-22

一天，老班气冲冲地走进教室对我们说：“太不像话了，这次考试竟然有60%的同学不及格！”　老师这句话里就有一个分位数的应用,60为0.6分位数。
什么是分位数？
在此我不想给出书上的定义，因为有那么多的同学发问怎么求分位数，正是因为不理解书上所写，好，怎么才能快速理解分位数呢？
一句话，分位数就是用概率作为依据将一批数据分开的那个点。
一、你首先得有数据
分位数是数据分析中常用的一个统计量，经过抽样得到一个样本值，以学生成成绩为例：
60,70,87,56,35,64,28,84,89,65.
二、p分位数
如果想在这10位同学中淘汰至少35%,同时让至少65%的同学晋级，你怎么选？
当然的想法是找一个数，小于等于这个数的同学至少有35%,大于等于这个数的同学至少有65%, 我们就把这个数记为0.35分位点，记为x0.35 ,见下图：

要想顺利地找到这个数，需要将数据排序：
28, 35, 56, 60，64, 65, 70,84, 87, 89
排序后上面十个数分别记为x(1)到x(10).
至少有35%,即至少有10*35%=3.5个学生，所以x0.35 ≥60=x(4);
至少有65%，即至少有10*65%=6.5个学生，所以x0.35≤60=x(4);
故二者取交集，令x0.35 =60.
以上是np不为整数的情况，如果np为整数，不妨设p=0.3
至少有30%,即至少有10*30%=3个学生，所以x0.3 ≥56=x(3);
至少有70%，即至少有10*70%=7个学生，所以x0.3≤60=x(4);
二者取交集，有两个值，一个是56,一个是60,如何选取？就取二者的平均值：
x0.3＝（56+60）/2=58. 参考技术A 分位数这个概念
通常都使用在概率论当中
就是指将一个随机变量
其概率分布范围分为几个等份的数值点
常用的有中位数（即二分位数）、四分位数、百分位数等
比如中位数就是指
这个点的两边其概率都是0.5

通过箱线图判断偏向

箱线图（Boxplot）也称箱须图（Box-whisker Plot），是利用数据中的五个统计量：最小值、第一四分位数、中位数、第三四分位数与最大值来描述数据的一种方法，它也可以粗略地看出数据是否具有有对称性，分布的分散程度等信息，特别可以用于对几个样本的比较。

在箱图中，最上方和最下方的线段分别表示数据的最大值和最小值，其中箱图的上方和下方的线段分别表示第三四分位数和第一四分位数，箱图中间的粗线段表示数据的中位数。另外，箱图中在最上方和最下方的星号和圆圈分别表示样本数据中的极端值。

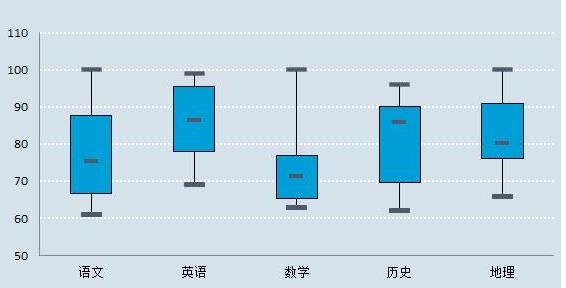
数据的形状

同一数轴上，几批数据的箱形图并行排列，几批数据的中位数、尾长、异常值、分布区间等形状信息便一目了然。在一批数据中，哪几个数据点出类拔萃，哪些数据点表现不及一般，这些数据点放在同类其它群体中处于什么位置，可以通过比较各箱形图的异常值看出。各批数据的四分位距大小，正常值的分布是集中还是分散，观察各方盒和线段的长短便可明了。

以上内容参考：百度百科-箱形图

参考技术A 箱线图（Boxplot）也称箱须图（Box-whisker Plot），是利用数据中的五个统计量：最小值、第一四分位数、中位数、第三四分位数与最大值来描述数据的一种方法，它也可以粗略地看出数据是否具有有对称性，分布的分散程度等信息，特别可以用于对几个样本的比较。

　1.直观明了地识别数据批中的异常值

　　一批数据中的异常值值得关注，忽视异常值的存在是十分危险的，不加剔除地把异常值包括进数据的计算分析过程中，对结果会带来不良影响；重视异常值的出现，分析其产生的原因，常常成为发现问题进而改进决策的契机。箱线图为我们提供了识别异常值的一个标准：异常值被定义为小于Q1－1.5IQR或大于Q3＋1.5IQR的值。虽然这种标准有点任意性，但它来源于经验判断，经验表明它在处理需要特别注意的数据方面表现不错。这与识别异常值的经典方法有些不同。众所周知，基于正态分布的3σ法则或z分数方法是以假定数据服从正态分布为前提的，但实际数据往往并不严格服从正态分布。它们判断异常值的标准是以计算数据批的均值和标准差为基础的，而均值和标准差的耐抗性极小，异常值本身会对它们产生较大影响，这样产生的异常值个数不会多于总数0.7%。显然，应用这种方法于非正态分布数据中判断异常值，其有效性是有限的。箱线图的绘制依靠实际数据，不需要事先假定数据服从特定的分布形式，没有对数据作任何限制性要求，它只是真实直观地表现数据形状的本来面貌；另一方面，箱线图判断异常值的标准以四分位数和四分位距为基础，四分位数具有一定的耐抗性，多达25%的数据可以变得任意远而不会很大地扰动四分位数，所以异常值不能对这个标准施加影响，箱线图识别异常值的结果比较客观。由此可见，箱线图在识别异常值方面有一定的优越性。

　　2.利用箱线图判断数据批的偏态和尾重

　　比较标准正态分布、不同自由度的t分布和非对称分布数据的箱线图的特征，可以发现：对于标准正态分布的大样本，只有 0.7%的值是异常值,中位数位于上下四分位数的中央,箱线图的方盒关于中位线对称。选取不同自由度的t分布的大样本，代表对称重尾分布，当t分布的自由度越小，尾部越重，就有越大的概率观察到异常值。以卡方分布作为非对称分布的例子进行分析，发现当卡方分布的自由度越小，异常值出现于一侧的概率越大，中位数也越偏离上下四分位数的中心位置，分布偏态性越强。异常值集中在较小值一侧，则分布呈现左偏态；；异常值集中在较大值一侧，则分布呈现右偏态。下表列出了几种分布的样本数据箱线图的特征（样本数据由SAS的随机数生成函数自动生成），验证了上述规律。这个规律揭示了数据批分布偏态和尾重的部分信息，尽管它们不能给出偏态和尾重程度的精确度量，但可作为我们粗略估计的依据。
3.利用箱线图比较几批数据的形状

　　同一数轴上，几批数据的箱线图并行排列，几批数据的中位数、尾长、异常值、分布区间等形状信息便昭然若揭。在一批数据中，哪几个数据点出类拔萃，哪些数据点表现不及一般，这些数据点放在同类其它群体中处于什么位置，可以通过比较各箱线图的异常值看出。各批数据的四分位距大小，正常值的分布是集中还是分散，观察各方盒和线段的长短便可明了。每批数据分布的偏态如何，分析中位线和异常值的位置也可估计出来。还有一些箱线图的变种，使数据批间的比较更加直观明白。例如有一种可变宽度的箱线图，使箱的宽度正比于批量的平方根，从而使批量大的数据批有面积大的箱，面积大的箱有适当的视觉效果。如果对同类群体的几批数据的箱线图进行比较，分析评价，便是常模参照解释方法的可视图示；如果把受测者数据批的箱线图与外在效标数据批的箱线图比较分析，便是效标参照解释的可视图示。箱线图结合这些分析方法用于质量管理、人事测评、探索性数据分析等统计分析活动中去，有助于分析过程的简便快捷，其作用显而易见。

希望能帮到你~ 参考技术B 首先异常值不能存在，或者相比较而言一两个也可以接受。
其次如果你的目标是越大越好，那么箱型图整体靠上，中位数横线靠上的比其他的好。
如果你的目标是越小越好，那么箱型图整体靠下，横线靠下的好。
总而言之就是矩形区域表示50%的数据所在，横线表示正态分布的那个顶峰所在的值。依据你是觉得50%分布比较重要还是数量顶峰所在的值的高低比较重要来选择。