什么是分位数,如何计算分位数?
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了什么是分位数,如何计算分位数?相关的知识,希望对你有一定的参考价值。
参考技术A 分位数是将总体的全部数据按大小顺序排列后,处于各等分位置的变量值。如果将全部数据分成相等的两部分,它就是中位数;如果分成四等分,就是四分位数;八等分就是八分位数等。四分位数也称为四分位点,它是将全部数据分成相等的四部分,其中每部分包括25%的数据,处在各分位点的数值就是四分位数。四分位数有三个,第一个四分位数就是通常所说的四分位数,称为下四分位数,第二个四分位数就是中位数,第三个四分位数称为上四分位数,分别用Q1、Q2、Q3表示。四分位数作为分位数的一种形式,在统计中有着十分重要的作用和意义,现就四分位数的计算做一详细阐述。一、资料未分组四分位数计算
第一步:确定四分位数的位置。Qi 所在的位置=i(n+1)/4,其中i=1,2,3。n表示资料项数。
第二步:根据第一步四分位数的位置,计算相应四分位数。
例1:某数学补习小组11人年龄(岁)为:17,19,22,24,25,
28,34,35,36,37,38。则三个四分位数的位置分别为:
Q1所在的位置=(11+1)/4=3,Q2所在的位置=2(11+1)/4=6,Q3所在的位置=3(11+1)/4=9。
变量中的第三个、第六个和第九个人的岁数分别为下四分位数、中位数和上四分位数,即:
Q1=22(岁)、Q2=28(岁)、Q3=36(岁)
我们不难发现,在上例中(n+1)恰好是4的整数倍,但在很多实际工作中不一定都是整数倍。这样四分位数的位置就带有小数,需要进一步研究。带有小数的位置与位置前后标志值有一定的关系:四分位数是与该小数相邻的两个整数位置上的标志值的平均数,权数的大小取决于两个整数位置的远近,距离越近,权数越大,距离越远,权数越小,权数之和应等于1。
例2:设有一组经过排序的数据为12,15,17,19,20,23,25,
28,30,33,34,35,36,37,则三个四分位数的位置分别为:
Q1所在的位置=(14+1)/4=3.75,Q2所在的位置=2(14+1)/4=7.5,Q3所在的位置=3(14+1)/4=11.25。
变量中的第3.75项、第7.5项和第11.25项分别为下四分位数、中位数和上四分位数,即:
Q1=0.25×第三项+0.75×第四项=0.25×17+0.75×19=18.5;
Q2=0.5×第七项+0.5×第八项=0.5×25+0.5×28=26.5;
Q3=0.75×第十一项+0.25×第十二项=0.75×34+0.25×35=34.25。
二、资料已整理分组的组距式数列四分位数计算
第一步:向上或向下累计次数(因篇幅限制,以下均采取向上累计次数方式计算);
第二步:根据累计次数确定四分位数的位置:
Q1的位置 = (∑f+1)/4,Q2的位置 = 2(∑f +1)/4,Q3的位置 = 3(∑f +1)/4
式中:∑f表示资料的总次数;
第三步:根据四分位数的位置计算各四分位数(向上累计次数,按照下限公式计算四分位数):
Qi=Li+■×di
式中:Li——Qi所在组的下限,fi——Qi所在组的次数,di——Qi所在组的组距;Qi-1——Qi所在组以前一组的累积次数,∑f——总次数。
例3:某企业工人日产量的分组资料如下:
根据上述资料确定四分位数步骤如下:
(1)向上累计方式获得四分位数位置:
Q1的位置=(∑f +1)/4=(164+1)/4=41.25
Q2的位置=2(∑f +1)/4=2(164+1)/4=82.5
Q3的位置=3(∑f +1)/4=3(164+1)/4=123.75
(2)可知Q1,Q2,Q3分别位于向上累计工人数的第三组、第四组和第五组,日产量四分位数具体为:
Q1=L1+■×d1=70+■×10=72.49(千克)
Q2=L2+■×d2=80+■×10=80.83(千克)
Q3=L3+■×d3=90+■×10=90.96(千克)
分位数回归—R语言实现
大家好,我是带我去滑雪,每天教你一个小技巧!
分位数回归—R语言实现
1、分位数基本介绍——什么是分位数?

2、分位数回归用途——为什么要使用分位数回归?
传统的线性回归模型描述了因变量的条件均值分布受自变量X的影响过程。其中,最小二乘法是估计回归系数的最基本方法。如果模型的随机误差项来自均值为零、方差相同的分布,那么回归系数的最小二乘估计为最佳线性无偏估计;如果随机误差项进一步服从正态分布,那么回归系数的最小二乘估计与极大似然估计一致,均为最小方差无偏估计。此时它具有无偏性、有效性等优良性质。
但是在实际的经济生活中,这种假设通常不能够满足。例如当数据中存在严重的异方差,或后尾、尖峰情况时,最小二乘法的估计将不再具有上述优良性质。最小二次估计假定解释变量x只能影响被解释变量的条件分布的均值的位置,不能影响其分布的刻度或形状的任何其他方面。分位数回归的条件更加宽松。
3、图形分析——如何进行分位数回归图像分析?
假如,现在有一个如下散点图分布的数据,对其进行普通的回归分析,得到:
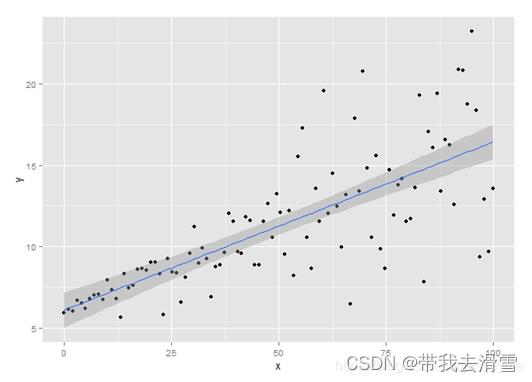
从拟合的曲线我们就可以看出问题了,原数据随着x增大,y的分布范围越来越大,可是因为普通的回归分析得到的是条件期望函数,也就是y的期望,所以平均即使y的分布变化了,平均来说y还是以同样的斜率稳定上升。
当我们使用0.9分位数回归,重新得出新函数图像:
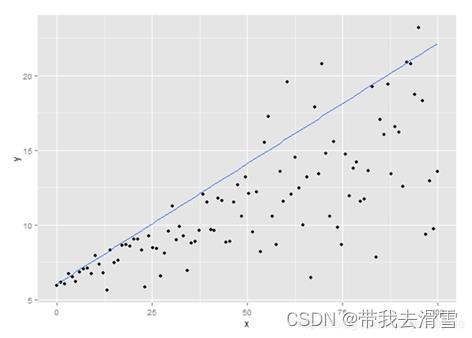
这次,比起普通的回归分析,就能进一步显示出y的变化幅度其实是增大了。所谓的0.9分位数回归,就是希望回归曲线之下能够包含90%的数据点(y),这也是分位数的概念,分位数回归是把分位数的概念融入到普通的线性回归而已。
进一步的我们可以画出不同的分位数回归曲线,这样才能能更加明显地反映出,随着x的增大,y的不同范围的数据是不同程度地变化的,而这个结论通过以前的回归分析是无法得到的,这就是分位数回归的作用。
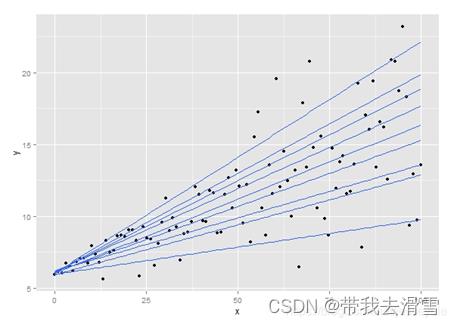
在实际研究中,例如研究社会的贫穷情况可能就会选择收入相对较低的群体即收入水平的低分位点,而研究制定税收政策会关注高收入人群即收入水平的高分位点。
4、分位数回归原理——如何进行分位数回归?



5、分位数回归的假设检验——能不能用?好不好?
分位数回归估计的检验包括两部分:一是与均值回归类似的检验,例如拟合优度检验、回归约束检验;二是分位数回归估计特色要求的检验,如斜率相等检验、斜率对称性检验。



6、简单线性分位数回归实例——分位数回归R实操
install.packages("quantreg")
library(quantreg)#导入分位数回归的包
data(engel)# 引入数据
mode(engel)#查看数据格式
names(engel)#查看变量名
head(engel)#查看数据的前五行
plot(engel$income,engel$foodexp)#画个散点图
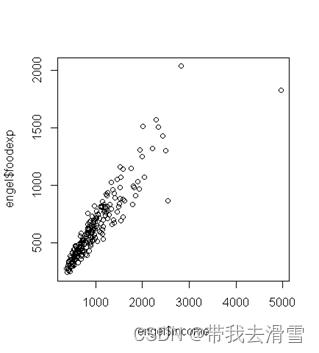
可以看出,数据随着x的增大,y的分布范围越来越大。
#简单验证一下因变量foodexp是否服从正态分布
plot(density(engel$foodexp))
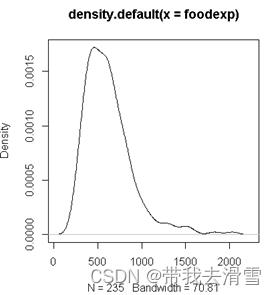
可以看出y是右偏分布。
qqnorm(engel$foodexp, main='QQ plot')
qqline(engel$foodexp, col='red', lwd=2)
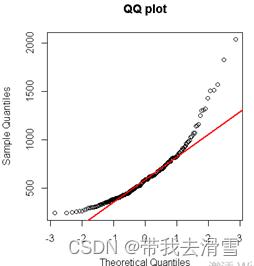
结果呈一条直线才能说明大致服从正态分布,显然因变量foodexp明显不服从正态分布,但是,分位数回归不要求y服从正态分布,不仅如此,而且分位数回归还对异常值点不敏感。
下面我们继续,为了对比,我们做一个均值回归,再做一个分位数回归。
#设置0.05, 0.25, 0.5, 0.75, 0.95五个分位点,并且rq函数进行分位数回归,这样可以得到五条分位数回归线
rq_result <- rq(foodexp ~ income, tau=c(0.05, 0.25, 0.5, 0.75, 0.95))
summary(rq_result,se="nid")#系数的假设检验,se指定用于计算标准误差的方法

#上面就是每个分位点下回归线的回归系数,做个图看一下
plot(income, foodexp, cex=0.25, type='n', xlab='income', ylab='foodexp')
points(income, foodexp, cex=0.5, col='blue')
abline(rq(foodexp~income, tau=0.5), col='blue')#加中位数数回归的直线
abline(lm(foodexp~income), lty=2, col='red')#加均值回归线
taus <- c(0.05, 0.1, 0.25, 0.75, 0.9, 0.95)#将分位数回归线加上去
for (i in 1:length(taus))
abline(rq(foodexp~income, tau=taus[i]), col='gray')

红线为传统均值回归线,其余的为分位数回归线。从上图,可以看到,分位数回归可以拟合出多条直线,这个对于我们数据分布比较复杂的时候,很有用处,每条线反应了不同档次下,自变量与因变量的关系。
rq_result2 <- rq(foodexp ~ income, tau=1:98/100)#选取更多的分位点并作图
plot(summary(rq_result2,se="nid"))
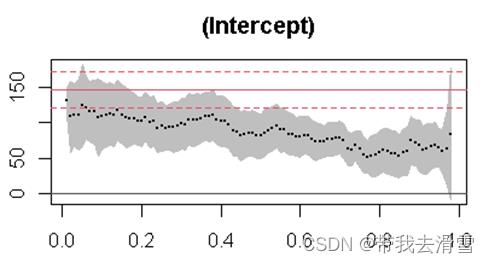
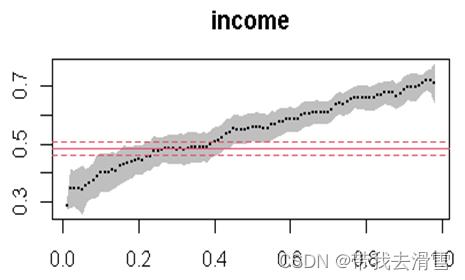
可以看到,随着分位点的增大,自变量income对因变量foodexp的影响效果是逐渐增大的。
往期精彩内容推介:
1、python常用统计分析包
https://blog.csdn.net/qq_45856698/article/details/129304015?spm=1001.2014.3001.5501
2、偏最小二乘估计优点与适用、原理、算法推导
https://blog.csdn.net/qq_45856698/article/details/129302607?spm=1001.2014.3001.5501
3、运用自回归滑动平均模型、灰色预测模型、BP神经网络三种模型分别预测全球平均气温,并进行预测精度对比(附代码、数据)
https://blog.csdn.net/qq_45856698/article/details/129286994?spm=1001.2014.3001.5501
4、运用python爬取股票的股吧评论、新闻报道(附完整代码)
https://blog.csdn.net/qq_45856698/article/details/129268092?spm=1001.2014.3001.5501
5、利用Python爬取房价信息(附代码)
https://blog.csdn.net/qq_45856698/article/details/129249555?spm=1001.2014.3001.5501
更多优质内容持续发布中,请移步主页查看。
点赞+关注,下次不迷路!
以上是关于什么是分位数,如何计算分位数?的主要内容,如果未能解决你的问题,请参考以下文章