cs231n 卷积神经网络与计算机视觉 5 神经网络基本结构激活函数总结

Posted 2020-07-14 bea_tree

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了cs231n 卷积神经网络与计算机视觉 5 神经网络基本结构激活函数总结相关的知识，希望对你有一定的参考价值。

1 引入

神经网络中的神经元的灵感来源于人脑，人体中大约有860亿个神经元，大约有 10^14 - 10^15 突触（synapses）. 每个神经元由树突dendrites接收信号轴突axon发射信号. 轴突又连接到其他神经单元的树突.突触强度synaptic strengths (权重w) 可以经过学习控制输入信号的输出是抑制还是激活( excitory (positive weight) or inhibitory (negative weight)) . 如果经过细胞体汇合之后的信号大于阈值，神经元就被激活（fire）, 通过树突释放信号（spike）. 计算模型中我们认为spike的时间并不重要，重要的是神经元间交流的频率. 我们使用激活函数activation function来模拟激活率firing rate ，通常我们使用sigmoid 函数σ作为激活函数（firing_rate = 1.0 / (1.0 + math.exp(-cell_body_sum))）,他可以将输入的数值转化为0到1之间的数.下图是生物神经元与数学中的神经元模型的对比：
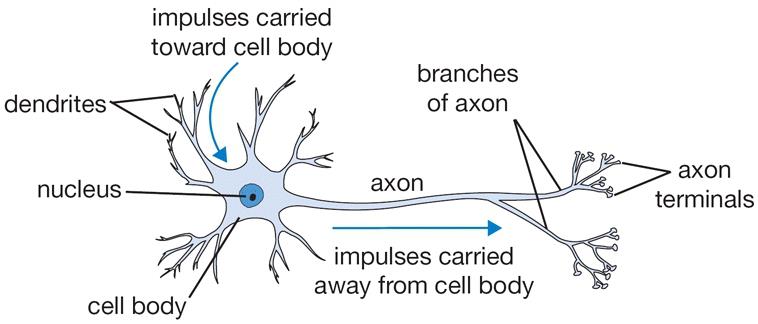
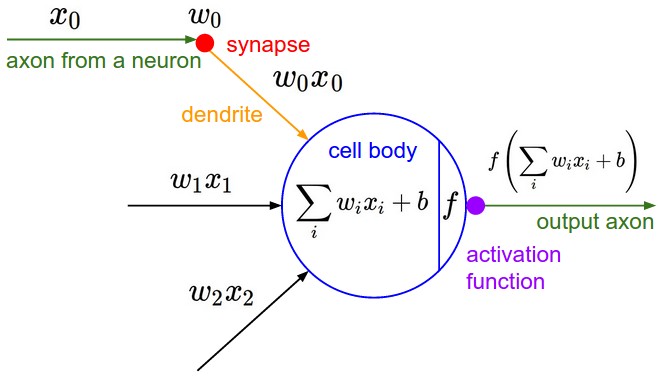
这里写图片描述
注意这里的激活函数需要用非线性函数，因为多个线性函数的叠加依然可以用一个线性函数表示，这样就失去了多层的意义。
一个数学模型中的神经元的作用过程大致的步骤是：
1. 输入x与权重w做内积 dot product
2. 内积结果输入激活函数
3. 从激活函数输出信号
其实这个过程与真正的生物过程相比弱爆了，只是一个很粗糙的模型，这里有两篇比较真正生物神经元的文章Current Opinion in Neurobiology及Dendritic Computation，这里还是简要说下与生物神经元的不同：
1. 神经元的种类有不同，性能不同；
2. 树突有着复杂的非线性过程；
3. 突触并不是一个单个的权重而已，他是一个非线性动态系统（non-linear dynamical system）；
4. 每个激励的发出时间也是很重要的，我们并没有对其进行建模；
5. 其他简化。

2 单神经元二分类器

二分类器是一种线性分类器，这里主要介绍了两种：
1. binary Softmax classifier，将 cross-entropy loss减少到两种即可，这也是logistic regression；
2. binary svm classifier，将cross-entropy loss 转化为max-margin hinge loss即可。
另外，这里的最终优化中也可以加入regularization，这里regularization的生物学解释是：生物神经元中的参数会被逐步遗忘gradual forgetting，所有的参数都有着向着0更新退化的趋势。

3 常用的激活函数汇总分析

总结如下：
这里写图片描述

3.1 sigmoid $\\sigma(x) = 1 / (1 + e^{-x})$

缺点：
1. Sigmoids saturate and kill gradients.首先看一下sigmoid的导数图像：
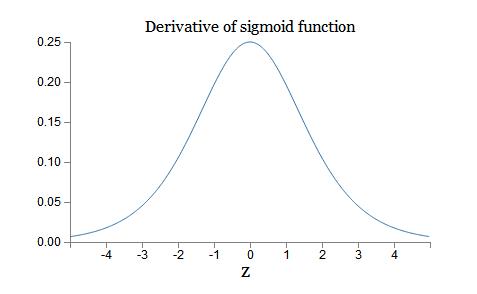
这里写图片描述
可以看到他的导数都是小于0.25的，那么在进行反向传播的时候如果多层都用sigmoid，其梯度相乘得到的结果会慢慢的趋近于0，也就是无法再进行权重的更新了，加上第一层的初始权重大多数比较随意，如果更新太慢势必影响最终效果，这叫做kill了Gradients，在UFLDL中叫作diffusion of gradients。另外在输入值初始设置很大时可能使很多神经元得到一个比较小的梯度，致使神经元不能很好的更新提前饱和，如下图：
这里写图片描述
2. outputs are not zero centered。
这样会造成在神经网络靠后层的输出的均值不为0. 如果神经元的输入数据都是正的值，那么权重w的值在反向传递的过程中的梯度会恒正或者横负(取决于整个表达式的梯度，exp(-wx)求导会得到一个-1). 这就会造成了w的z型更新.然后如果我们将多个或者或负的梯度结合起来就会使这种情况有所缓解，总的来说这个缺点比上一个要小一些。
这里写图片描述
3.另外指数形式计算比较复杂

3.2 tanh 双曲正切 $\\text {tanh}= (e^x-e^{-x})/ (e^x + e^{-x})$

他的其实可以看做是sigmoid的缩放版，他的公式可以写成 $\\tanh(x) = 2 \\sigma(2x) -1$ ,他相对于sigmoid的好处是他的输出的均值为0，克服了第二点缺点。但是当饱和的时候还是会kill gradient。

3.3 ReLU $f(x) = \\max(0, x)$

The Rectified Linear Unit 最近几年比较受欢迎的一个激活函数。
他的优缺点主要有：
- (+)无饱和区，收敛快.
- (+) 计算简单.
- (-)但是ReLU有时候会比较脆弱，脆弱到die。我们看到如果变量的更新太快，还没有找到最佳值，就进入小于零的分段就会使得梯度变为0，无法更新直接死掉了，所以应该仔细控制learning rate，如果控制不好可能有40%的神经单元误入死区。
- 另外他的输出也不是均值为零0的。

3.4 Leaky ReLU $f(x) = \\mathbb{max}(0.001x,x)$

他的公式是 $f(x) = \\mathbb{max}(\\alpha x,x)$ ,其中 $\\alpha$ 为较小的值如0.001.这样一来到了小于零的时候其梯度不再为0，修正了ReLU的缺点。这篇文章（Kaiming He et al., 2015）中介绍了其好处。

3.5 Exponential Linear Units (ELU)

其公式为：
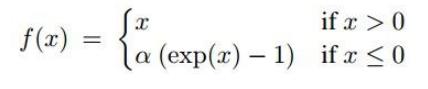
这里写图片描述
与其他几种激活函数的比较如图：

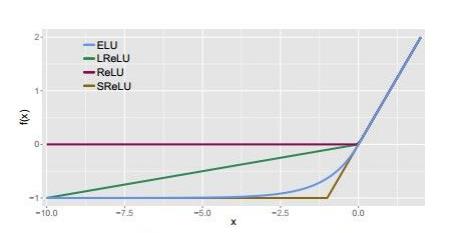
他的优点除了LReLu之外还有输出结果接近于零均值的良好特性。
其缺点为因为函数指数项所以计算难度会增加。

3.6 Maxout $\\max(w_1^Tx+b_1, w_2^Tx + b_2)$

由Goodfellow 等于2013年引入,可以看出他是ReLU和LReLU的一般化公式（如ReLU就是将w1和b1取为0）。所以他用于ReUL的优点而且没有死区，但是它的参数数量却增加了一倍。

以上就是基本的激活函数类型，虽然理论上可以将他们混合使用，但是基本没有这么干的，这里再一次粘一下几个激活函数的样子：
这里写图片描述
有时候选择太多也很让人纠结，我们该如何选择呢？

使用ReLU吧. 但是要注意learning rates，爱她保护她
也可以尝试 Leaky ReLU / Maxout / ELU
可以试试tanh 不要抱太大希望
不要用sigmoid了

4 神经网络结构

4.1Layer-wise organization 层级连接结构

他是层级连接的结构（一层的输出也是另外一层的输入），没有首位相接的循环. 最常见的形式如下图所示，单层之间的神经元并没有连接，但是多层之间的连接确实全部链接的, 这种连接形式叫作 fully-connected layer:
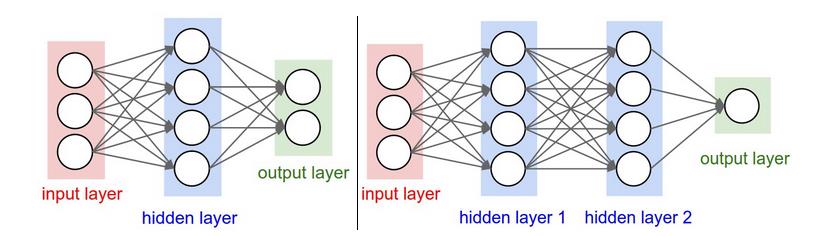
这里写图片描述
命名规则：我们约定N层神经网络中的N不包括输入层. 所以输入层直接连接输出层的就是单层神经网络，所以有时候也说t logistic regression或者 SVMs也是 single-layer Neural Networks中的一种. 我们将有多个层级的神经网络叫作人工神经网络“Artificial Neural Networks” (ANN) 或者多层神经网络“Multi-Layer Perceptrons” (MLP).
输出层：输出层不再有激活函数了（或者可以认为他有线性的激活函数），一般直接得到概率或者其他结果。
网络的size：一般会以神经网络的单元的数量或者参数的数量来衡量，上图中左侧含有6个单元，3x4+4x2个w及4+2个b，一共26个参数。另外一般的卷积神经网络要包含约上亿个参数，由10-20层神经网络组成，但是通过参数分享等方法可以有效提高计算的效率。

4.2 前馈计算示例

Repeated matrix multiplications interwoven with activation function. 将神经网络用上面的层级形式表示的好处之一就是可以用矩阵方便的操作. 以上面的三层神经网络为例输入是[3x1] 向量. 第一层的权重 W1 可以处存在 [4x3]的矩阵上, 偏置biases b1, 是 [4x1]向量. 所以每个神经元都会有一行权重与之对应，我们可以使用矩阵内积的形式np.dot(W1,x)来表示激活函数的输入值. 整个三层网络就可以表示为三个矩阵的乘积与激活函数作用的过程，例如三层网络的作用过程如下：

# forward-pass of a 3-layer neural network:
f = lambda x: 1.0/(1.0 + np.exp(-x)) # activation function (use sigmoid)
x = np.random.randn(3, 1) # random input vector of three numbers (3x1)
h1 = f(np.dot(W1, x) + b1) # calculate first hidden layer activations (4x1)
h2 = f(np.dot(W2, h1) + b2) # calculate second hidden layer activations (4x1)
out = np.dot(W3, h2) + b3 # output neuron (1x1)没有激活函数噢

Representational power

神经网络（with fully-connected layers）都是可以看做是有参数化网络的函数，那么这个函数的表达能力如何呢？有他不能表达的么？可以证明含有一层隐含层的网络就可以近似表达任何连续函数了.相关证明 Approximation by Superpositions of Sigmoidal Function 1989 (pdf), 还有一个直观的解释来自 Michael Nielsen) （ Michael Nielsen的整套教程都很好，有时间的话我想把它翻译成中文）。
既然一层就可以表达为什么需要多层或者深层呢？因为尽管数学上可以证明两层神经网络可以表达足够的信息但是实际应用中它可不够. 之前的文章也提到过，多层神经网络可以减少神经元的个数实际应用这他的作用效果更好.
另外普通的神经网络三层比两层要好一点，但是有时候4层5层或者更深的层次并没有什么作用，但是在卷积神经网络中往往十多层的网络表现较好。
以下是一些拓展阅读：
- Deep Learning book in press by Bengio, Goodfellow, Courville, in practicular Chapter 6.4.
- Do Deep Nets Really Need to be Deep?
- FitNets: Hints for Thin Deep Nets

Setting number of layers and their sizes

如何选择神经网络的层数和神经元数量呢？首先层数和神经元数量的增加可以增加神经网络的表达能力，下图是使用两层神经网络的二分类问题：
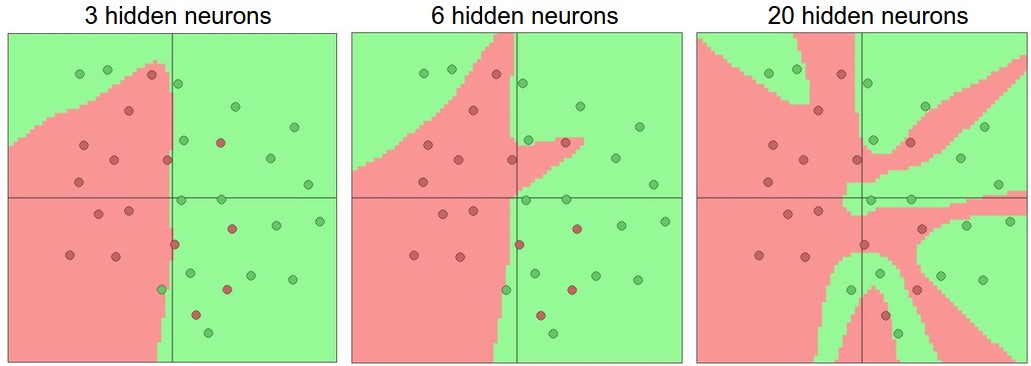
这里写图片描述
可见隐藏层单元数量越多越能表达复杂的函数。这个栗子的演示在这里。

我们可以看到在20个隐藏单元时过拟合了，把一些应该属于outliers (noise)的点也包含了，那么实际中我们是不是需要为了避免过拟合，增加泛化能力尽量使用少的层数和单元数呢？其实不然我们有很多可以使用的方法来控制过拟合比如L2 regularization, dropout, input noise。下图是对隐含层有20个神经单元时的二范数的规则化结果：
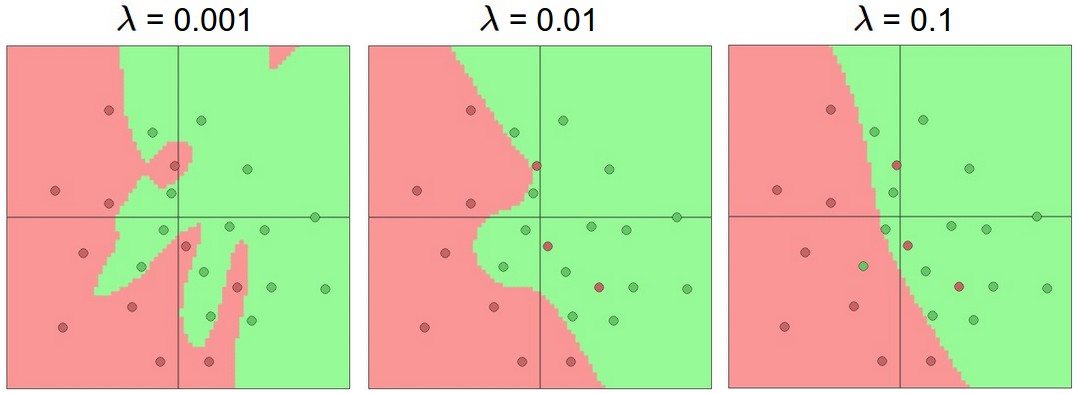
这里写图片描述
案例地址点这里。

另外使用size比较小的网络还有一个缺点：较小的神经网络在使用梯度下降等local methods得到的结果往往不稳定不准确。虽然较小的神经网络会有更少的极值，但是这些极值的质量一般很差，而虽然大规模的神经网络的极值多但是他们的质量往往比较好，最然可能得到的结果不是真正的最值但是往往差距比较小，神经网络时非凸函数，数学研究要难一些，有兴趣的可以看看arXiv上的文章 The Loss Surfaces of Multilayer Networks.