CS231n 卷积神经网络与计算机视觉 6 数据预处理权重初始化规则化损失函数等常用方法总结

Posted 2020-07-14 bea_tree

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了CS231n 卷积神经网络与计算机视觉 6 数据预处理权重初始化规则化损失函数等常用方法总结相关的知识，希望对你有一定的参考价值。

1 数据处理

首先注明我们要处理的数据是矩阵X，其shape为[N x D] (N =number of data, D =dimensionality).

1.1 Mean subtraction 去均值

去均值是一种常用的数据处理方式.它是将各个特征值减去其均值，几何上的展现是可以将数据的中心移到坐标原点，Python中的代码是 X -= np.mean(X, axis = 0). 对于图像处理来说，每个像素的值都需要被减去平均值 ( X -= np.mean(X)), 也可以分别处理RGB三个通道。

1.2 Normalization 标准化

normalization是将矩阵X中的Dimensions都保持在相似的变化范围之内，有两种实现形式：
1. 先使用上一步，使均值为0，然后除以标准差X /= np.std(X, axis = 0)
2. 在数据不再同一范围，而且各个维度在同一范围内对算法比较重要时，可以将其最大最小值分别缩放为1和-1.
对于图像处理而言因为一般数据都在0-255之间所以不用再进行这一步了。
下面是数据处理的方式对比：
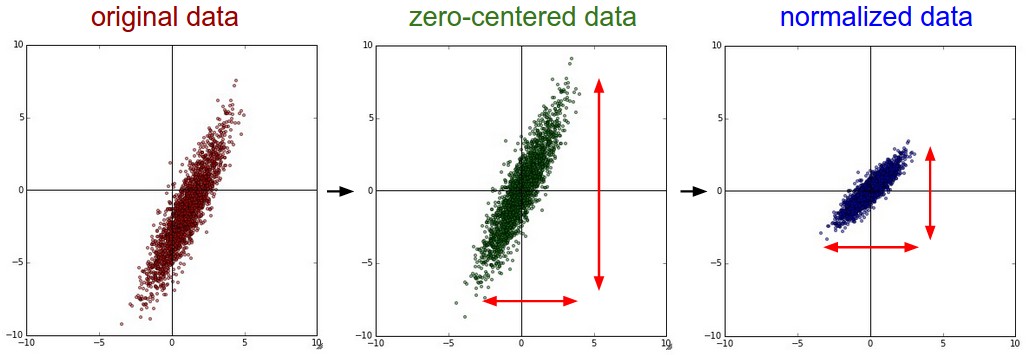
这里写图片描述

1.3 PCA和whitening

1.3.1 PCA

由于计算需要，需要实现进行前面所说的均值0化。
PCA要做的是将数据的主成分找出。流程如下：
1. 计算协方差矩阵
2. 求特征值和特征向量
3. 坐标转换
4. 选择主成分
首先我们需要求出数据各个特征之间的协方差矩阵，以得到他们之间的关联程度，Python代码如下：

# Assume input data matrix X of size [N x D]
X -= np.mean(X, axis = 0) # zero-center the data (important)
cov = np.dot(X.T, X) / X.shape[0] # get the data covariance matrix，公式含义可按照协方差矩阵的定义得到

其中得到的矩阵中的第（i,j）个元素代表第i列和第j列的协方差，对角线代表方差。协方差矩阵是对称半正定矩阵可以进行SVD分解：

U,S,V = np.linalg.svd(cov)

U 的列向量是特征向量， S 是对角阵其值为奇异值也是特征值的平方.奇异值分解的直观展示：
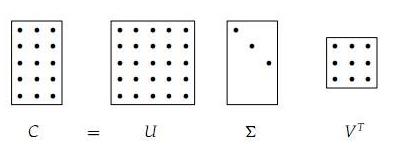
这里写图片描述
具体可以看这篇博客和麻省理工的公开课。
我们可以用特征向量（正交且长度为1可以看做新坐标系的基）右乘X（相当于旋转坐标系）就可以得到新坐标下的无联系（正交）的特征成分：

Xrot = np.dot(X, U) # decorrelate the data

注意上面使用的np.linalg.svd(）已经将特征值按照大小排序了，这里仅需要取前几列就是取前几个主要成分了（实际使用中我们一般按照百分比取），代码：

Xrot_reduced = np.dot(X, U[:,:100]) # Xrot_reduced becomes [N x 100]

1.3.2 白化

白化要做的就是在PCA的基础上再除以每一个特征的标准差，以使其normalization，其标准差就是奇异值的平方根：

# whiten the data:
# divide by the eigenvalues (which are square roots of the singular values)
Xwhite = Xrot / np.sqrt(S + 1e-5)

但是白化因为将数据都处理到同一个范围内了，所以如果原始数据有原本影响不大的噪声，它原本小幅的噪声也会放大到与全局相同的范围内了。
另外我们为了防止出现除以0的情况在分母处多加了0.00001，如果增大他会使噪声减小。
白化之后得到是一个多元高斯分布。
上面两种处理的结果如下：
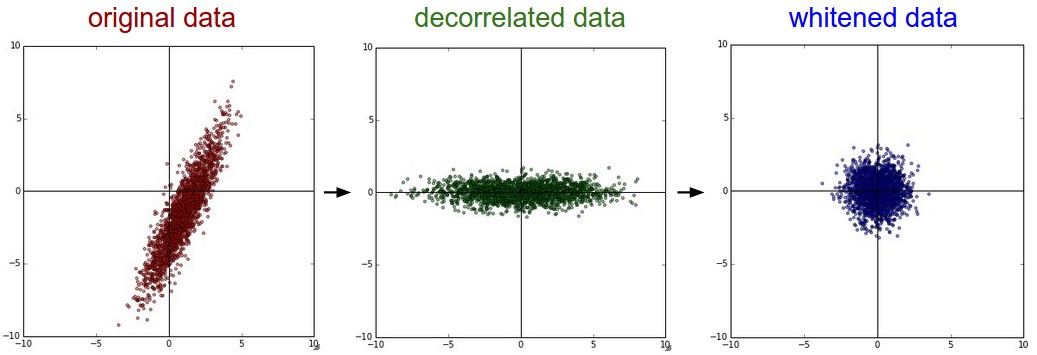
这里写图片描述
可以看出经过pca的去关联操作，将原始数据的坐标旋转，并且可以看出x方向的信息量比较大，如果只选一个特征，那么就选横轴方向的特征，经过白化之后数据进入了相同的范围。
下面以处理之前提到过的CIFAR-10为例，看PCA和Whitening的作用：
这里写图片描述
左边是原始图片，每张图片都是一个3072维的一行向量，经过PCA之后选取144维最重要的特征（左2），将特征转化到原来的坐标系U.transpose()[:144,:]得到了降维之后的图形（左3），图形变模糊了，说明我们的主要信息都是低频信息，关于高低频的含义在下一段展示一下，图片模糊了但是主要成分都还在，最后一个图是白化之后再转换坐标系之后的结果。

1.3.3 图像的高频分量和低频分量

形象一点说：亮度或灰度变化激烈的地方对应高频成分，如边缘；变化不大的地方对于低频成分，如大片色块区画个直方图，大块区域是低频，小块或离散的是高频，一幅图象，你戴上眼镜，盯紧了一个地方看到的是高频分量
摘掉眼镜，眯起眼睛，模模糊糊看到的就是低频分量。（参考了这篇文章）
上面的白化之后低频分量被大大的减弱了，但是高频分量却留了下来。

1.3.4 注意事项

CNN不需要进行PCA和白化，这里只是普及数据预处理的方法。
CNN只需要均值0化就行了
注意进行所有的预处理时训练集、验证集和测试集都要使用相同的处理方法，比如在减去均值时，三个数据集需要减去相同的值。

2 权重初始化

在训练上面我们处理好的数据之前，还需要对神经网络的权重进行初始化。

2.1 为什么不是0？

首先说明下，初始权重不能全为0.经过适当的数据预处理之后我们可以合理的认为大约有一般的权重是正的另一半是负的，我们可能认为他的均值可能为0，但是绝对不能将其全部都设为0，严格来说不能把所有的权重都设置为相同的值，以前在反向传播中已经提到过，如果所有的权重相同，如下图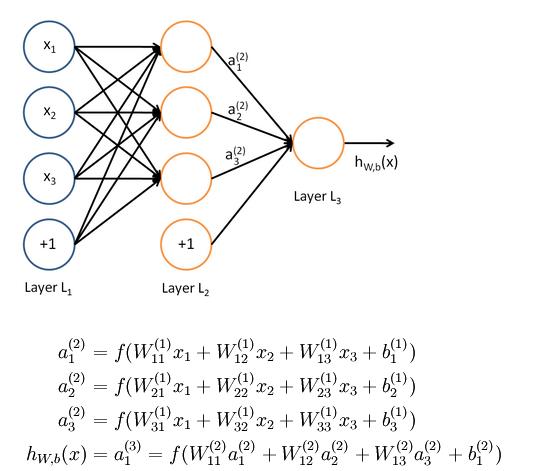：这里写图片描述

那么所有的神经单元都会得到相同的结果，另外在求梯度时候得到的梯度也是全部都一样（还可以看知乎的相关问题）。

2.2 小随机数

如2.1所说，我们还是想让权重的接近于0，那么取一个很小的接近于0的随机数可以么？例如这样设置：

W = 0.01* np.random.randn(D,H)

这样既满足各个初始值不一样又可以使其接近于零，但是这样还是不好，如果你看过上面提到的博客和知乎之后就会发现返现传播的梯度大小是和权重的值成正比的，所以如果其值很小那么得到的梯度也是很小的。小型网络也许还可以，但是通过几层网络之后会产生激活值的非均匀分布：
如一个10层每层500个单元的神经网络，初始化设置为W = 0.01* np.random.randn(D,H),激活函数为tanh，就会发现每层得到的激活值如下：
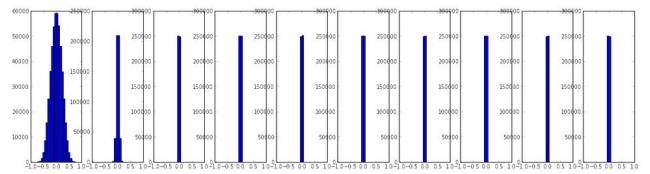
这里写图片描述
可以看到后面基层激活值全部都成了0.毕竟w乘以x然后经过激活函数再经过乘以w得到的结果会越来越接近于0.梯度也会变的很小。
如果我们将其值变大些W = 1* np.random.randn(D,H)，得到的结果又会变为：
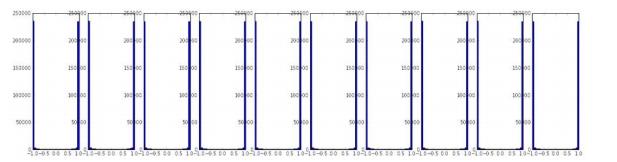，所有的又接近于1和-1，那么每个激活函数的导数由接近于0了。到底该怎么设置呢？看下面

2.3 方差校准

经验告诉我们如果初始时每个单元的输出都有着相似的分布会使收敛速度增大。而上面使用随机的方式会使得各个单元的输出值的分布产生较大的变化，新假设使用线性激活函数，探究输入与输出的分布的关系。
首先我们设输入是x，xw的内积是s，现在看他们方差的关系：

Var (s) = Var (\sum i n w i x i) = \sum i n Var (w i x i) = \sum i n [E (w i)] 2 Var (x i) + E [(x i)] 2 Var (w i) + Var (x i) Var (w i) = \sum i n Var (x i) Var (w i) = (n Var (w)) Var (x) 以上是关于CS231n 卷积神经网络与计算机视觉 6 数据预处理 权重初始化 规则化 损失函数 等常用方法总结的主要内容，如果未能解决你的问题，请参考以下文章 cs231n 卷积神经网络与计算机视觉 5 神经网络基本结构 激活函数总结 CS231n 卷积神经网络与计算机视觉 7 神经网络训练技巧汇总 梯度检验 参数更新 超参数优化 模型融合 等 全球名校课程作业分享系列--斯坦福计算机视觉与深度学习CS231n之基于cifar10的卷积神经网络实践 斯坦福CS231n—深度学习与计算机视觉----学习笔记 课时14&&15 斯坦福CS231n—深度学习与计算机视觉----学习笔记 课时26&&27 CS231n笔记6--Convolution与Pooling

CS231n 卷积神经网络与计算机视觉 6 数据预处理 权重初始化 规则化 损失函数 等常用方法总结