7-3 树的同构

Posted 2020-10-23 我只有一件白T恤

7-3 树的同构（25 分）

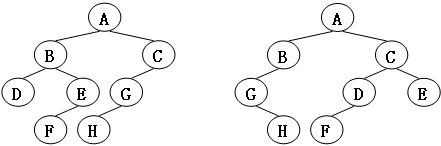
给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2，则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的，因为我们把其中一棵树的结点A、B、G的左右孩子互换后，就得到另外一棵树。而图2就不是同构的。

 

 

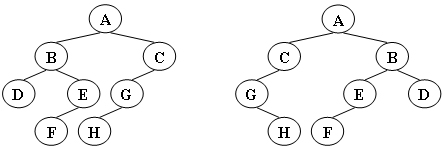
图1

图2

现给定两棵树，请你判断它们是否是同构的。

 

输入格式:

输入给出2棵二叉树树的信息。对于每棵树，首先在一行中给出一个非负整数N (≤10)，即该树的结点数（此时假设结点从0到N?1编号）；随后N行，第i行对应编号第i个结点，给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空，则在相应位置上给出“-”。给出的数据间用一个空格分隔。注意：题目保证每个结点中存储的字母是不同的。

输出格式:

如果两棵树是同构的，输出“Yes”，否则输出“No”。

输入样例1（对应图1）：

8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -

输出样例1:

Yes

输入样例2（对应图2）：

8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4

输出样例2:

No

思路：离散数学学的不错的话这个应该很简单吧，用两个字符数组，将两树的结点字母按输入次序分别保存起来，每棵树中有连接的两个结点用二维数组记录起来（保存图一样的操作），然后用树一的二维数组去遍历，遍历到值为1的情况，就去遍历树二的二维数组查看是否值也为1，一旦出现不是的情况就输出No，全部循环结束后输出Yes。

#include<stdio.h>
#include<string.h>
#include<iostream>
using namespace std;
int main()
{
    int n1, n2, map1[20][20], map2[20][20];                //开大了点
    memset(map1, 0, sizeof(int)* 400);                        //初始化数组
    memset(map2, 0, sizeof(int)* 400);

    char a[15], b[15];
    cin >> n1;
    for (int i = 0; i < n1; i++)
    {
        char temp1, temp2;
        cin >> a[i] >> temp1 >> temp2;
        map1[i][i] = 1;
        if (temp1 != ‘-‘){                                //构建图
            map1[i][temp1 - ‘0‘] = 1;
            map1[temp1 - ‘0‘][i] = 1;
        }
        if (temp2 != ‘-‘){
            map1[i][temp2 - ‘0‘] = 1;
            map1[temp2 - ‘0‘][i] = 1;
        }
    }
    cin >> n2;
    for (int i = 0; i < n2; i++)
    {
        char temp1, temp2;
        cin >> b[i] >> temp1 >> temp2;
        map2[i][i] = 1;
        if (temp1 != ‘-‘){                            //构建图
            map2[i][temp1 - ‘0‘] = 1;
            map2[temp1 - ‘0‘][i] = 1;
        }
        if (temp2 != ‘-‘){
            map2[i][temp2 - ‘0‘] = 1;
            map2[temp2 - ‘0‘][i] = 1;
        }
    }

    if (n2 != n1){
        cout << "No" << endl;
        return 0;
    }

    for (int i = 0; i < n1; i++)
    for (int j = 0; j < n1; j++)
    {
        int m = 19, n = 19;                    //这个防止了只有一个结点，结构相同而数据不同的情况，
        if (map1[i][j] == 1){                    //也就是在??，转换的时候找不到的情况

            for (int ii = 0; ii < n2;ii++)        //两个图之间的转化
            if (a[i] == b[ii])m = ii;
            for (int jj = 0; jj < n2;jj++)
            if (a[j] == b[jj])n = jj;
            if (map2[m][n] != 1)
            {
                cout << "No" << endl;
                return 0;
            }
        }
    }
    
    cout << "Yes" << endl;
    return 0;
}