洛谷 P3371 模板单源最短路径

Posted 2020-10-13 一蓑烟雨任生平

P3371 【模板】单源最短路径

题目描述

如题，给出一个有向图，请输出从某一点出发到所有点的最短路径长度。

输入输出格式

输入格式：

 

第一行包含三个整数N、M、S，分别表示点的个数、有向边的个数、出发点的编号。

接下来M行每行包含三个整数Fi、Gi、Wi，分别表示第i条有向边的出发点、目标点和长度。

 

输出格式：

 

一行，包含N个用空格分隔的整数，其中第i个整数表示从点S出发到点i的最短路径长度（若S=i则最短路径长度为0，若从点S无法到达点i，则最短路径长度为2147483647）

 

输入输出样例

输入样例#1： 复制

4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4

输出样例#1： 复制

0 2 4 3

说明

时空限制：1000ms,128M

数据规模：

对于20%的数据：N<=5，M<=15

对于40%的数据：N<=100，M<=10000

对于70%的数据：N<=1000，M<=100000

对于100%的数据：N<=10000，M<=500000

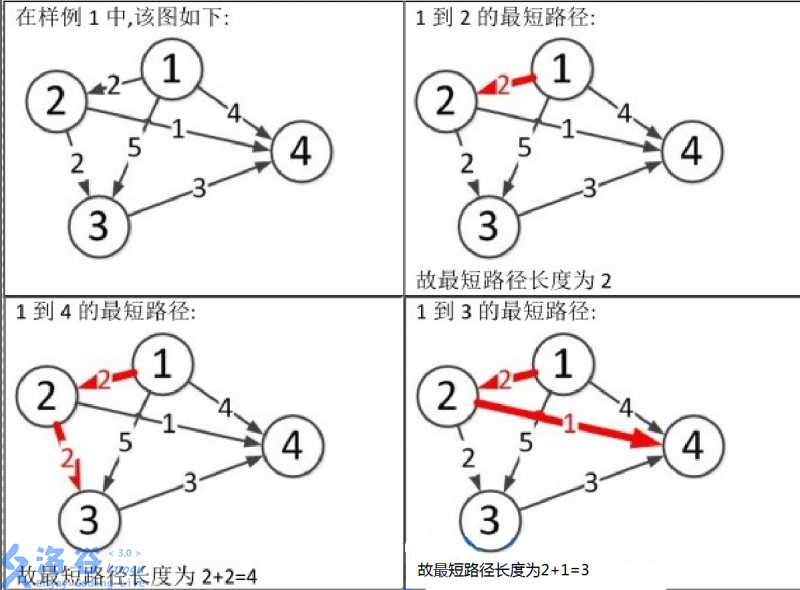
样例说明：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<deque>
#define MAXN 500010
using namespace std;
deque<int>que;
int n,m,s,vis[MAXN],num[MAXN],dis[MAXN];
int tot,to[MAXN],from[MAXN],net[MAXN],cap[MAXN];
void add(int u,int v,int w){
    to[++tot]=v;net[tot]=from[u];cap[tot]=w;from[u]=tot;
}
bool spfa(int s){
    for(int i=1;i<=n;i++)    dis[i]=2147483647;
    que.push_back(s);
    vis[s]=1;num[s]++;dis[s]=0;
    while(!que.empty()){
        int now=que.front();
        que.pop_front();
        vis[now]=0;
        for(int i=from[now];i;i=net[i])
            if(dis[to[i]]>dis[now]+cap[i]){
                dis[to[i]]=dis[now]+cap[i];
                if(!vis[to[i]]){
                    if(dis[to[i]]>dis[que.front()])
                        que.push_back(to[i]);
                    else
                        que.push_front(to[i]); 
                    vis[to[i]]=1;
                    num[to[i]]++;
                    if(num[to[i]]>n)
                        return false;
                }
            }
    }
    return true;
}
int main(){
    cin>>n>>m>>s;
    for(int i=1;i<=m;i++){
        int u,v,w;
        cin>>u>>v>>w;
        add(u,v,w);
    }
    if(spfa(s))
        for(int i=1;i<=n;i++)
            cout<<dis[i]<<" ";
}

spfa 最短路

 

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#include<queue>
#define MAXN 500010
using namespace std;
struct nond{
    int number,dis;
    bool operator < (nond b) const{
        return dis>b.dis;
    }
};
int n,m,s,dis[MAXN];
int tot,to[MAXN],net[MAXN],from[MAXN],cap[MAXN];
void add(int u,int v,int w){
    to[++tot]=v;net[tot]=from[u];cap[tot]=w;from[u]=tot;
}
void dijkstra(int x){
    priority_queue<nond>que;
    for(int i=1;i<=n;i++)    dis[i]=2147483647;
    dis[x]=0;
    que.push((nond){x,0});
    while(!que.empty()){
        nond now=que.top();
        que.pop();
        if(dis[now.number]!=now.dis)    continue;
        for(int i=from[now.number];i;i=net[i])
            if(dis[to[i]]>dis[now.number]+cap[i]){
                dis[to[i]]=dis[now.number]+cap[i];
                que.push((nond){to[i],dis[to[i]]});
            }
    }    
}
int main(){
    cin>>n>>m>>s;
    for(int i=1;i<=m;i++){
        int u,v,w;
        cin>>u>>v>>w;
        add(u,v,w);
    }
    dijkstra(s);
    for(int i=1;i<=n;i++)
        cout<<dis[i]<<" ";
}

heap优化的dij