快速幂||取余运算 （分治算法）

Posted 2020-10-11

#include<iostream>
using namespace std;

long b,p,k;
long skt=1;
int we,tsm;

int ksm(long b,long p,long k)
{
    while(p)
    {
    if(p%2!=0)
    {
    skt=skt*b%k;//之所以不用p=p-1是因为后面的位运算中p=p>>1，相当于p=p/2，多出的那个1被自动消去了，所以p=p-1可写可不写
    }
    b=b*b%k;//重初始化，新的式子是（b*b mod k）的p/2次方 mod k
    p=p>>1;//相当于p=p/2，当p=1时p位移为0
    }
    return skt%k;
}

int main()
{
    cin>>b>>p>>k;
    cout<<b<<"^"<<p<<" mod "<<k<<"="<<ksm(b,p,k);
}

快速幂

　　

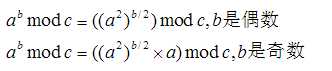
　　上面的公式，是快速幂算法的核心思路

　　实力分析：

　　　　可以用分治的思想简单进行快速幂的运算：

1. 当指数b为奇数时，则将其转为偶数，b=b-1，ans*=b
2. 当指数b为偶数时，b=b/2，a=a*a，由中国剩余定理知：（a*b）mod c=（a mod c）*（b mod c）

　　新的式子即为（a*a mod c）的b/2次方 mod c

　　当指数为1时，通过步骤1就可以将指数化为0，接下来求ans*b%c即出答案