树状数组 学习笔记

Posted 2020-10-09

树状数组可以用来求区间元素的和。

与前缀和做法不同，它支持值的修改。

比如说，现在我有一个数列a，要求你维护这个数列，使其支持两个操作。

1.改变数列第k项的值

2.查询从第i项到第j项的总值

 

暴力做法总是过不了所有点的，如果使用暴力，虽然操作1是O(1)的，但是操作2是O(n)的，没人对此复杂度满意。

 

假设原数列为a，我们的树状数组为c，那么，应该有下图的情况。

可以看出，每一个叶节点对应数组中的某个元素。

c[i]为第i列树上最高的那个点。

数组c就是树状数组。

 　　

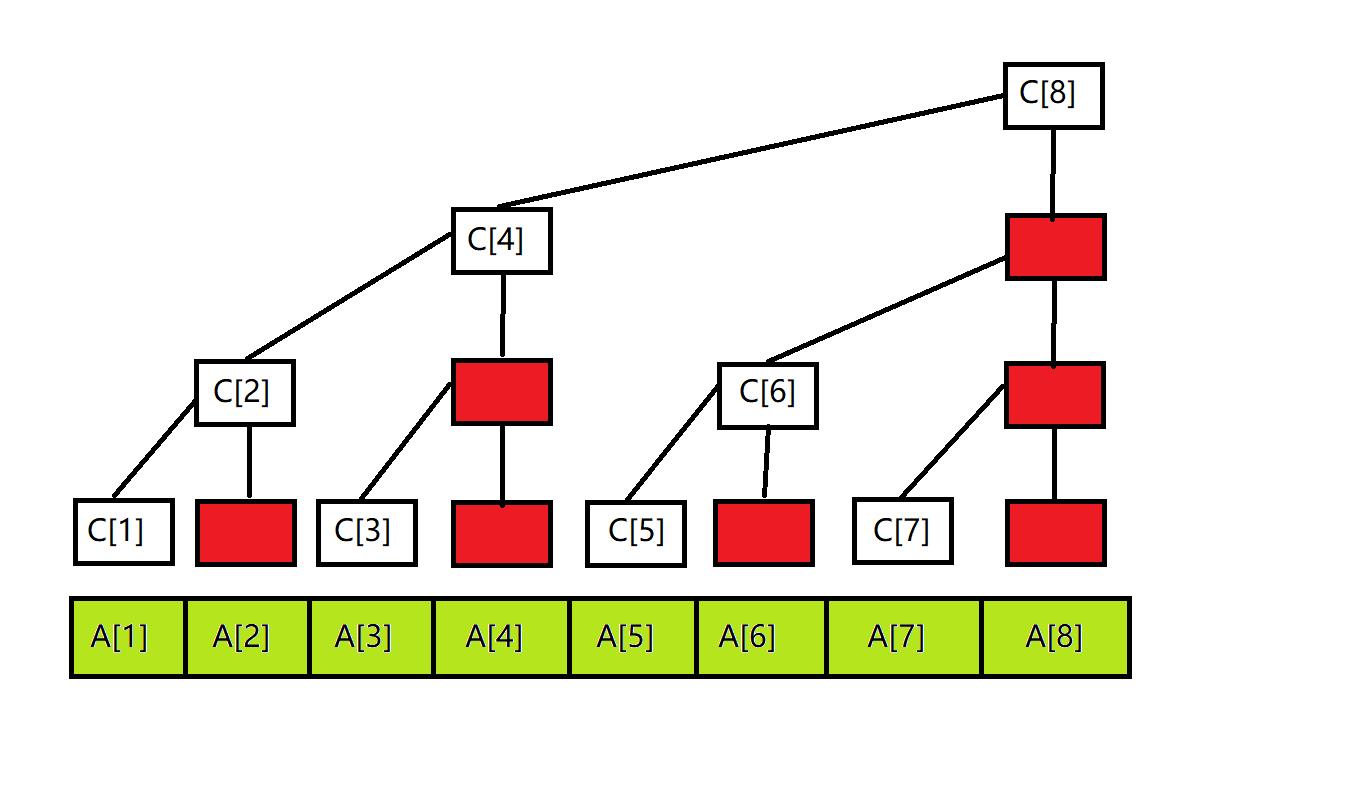
（红色的点实际上是不存在的，但是为了美观我还是画上了）

（据说线段树就是再把这些右儿子补回来）

不难看出

对于每一个c[i],其值总是决定于其两个子节点，也就是每一个c[i]都是两个子节点的值的和。

现在有一个特殊操作，把下标转化成二进制，就有下图所示的样子

 　　

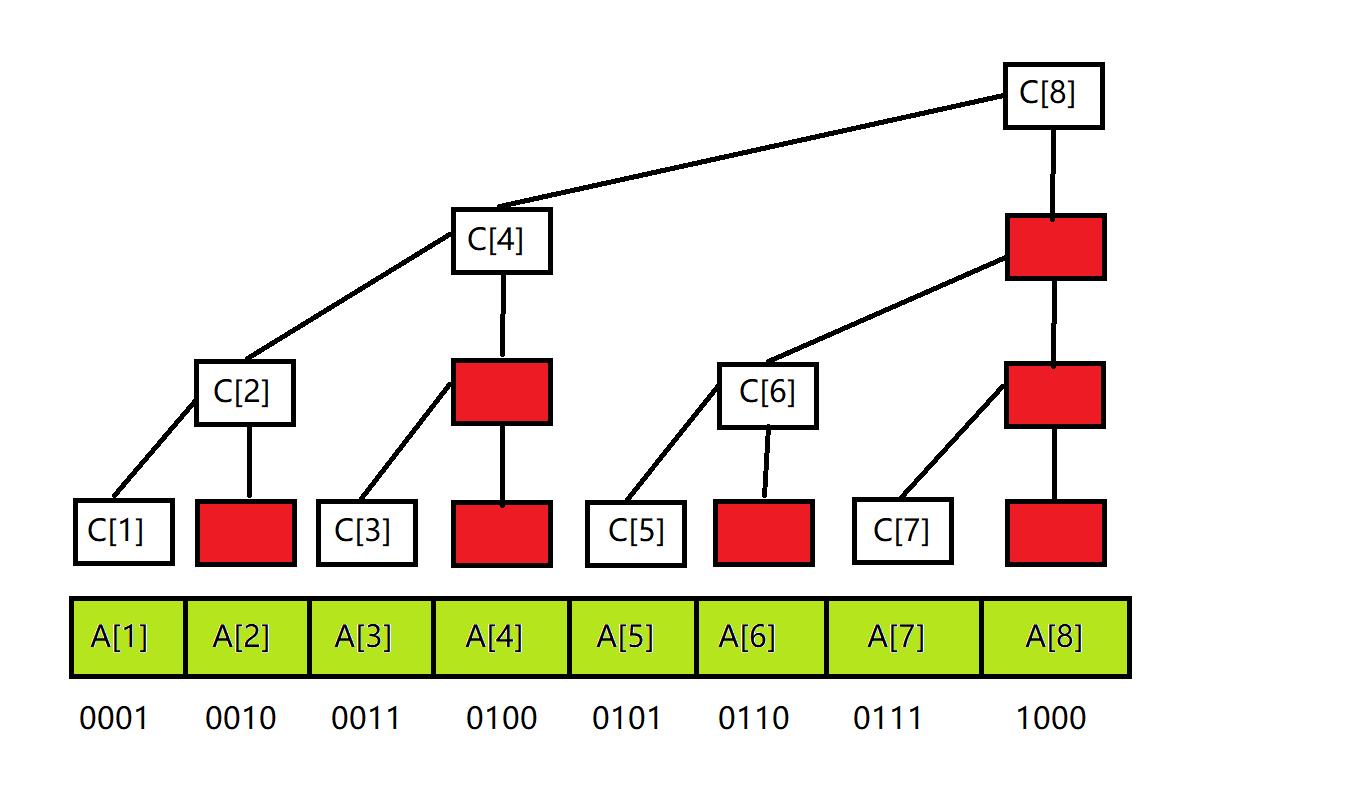
可以发现，叶节点的二进制位，其最低位必定是1，我们约定，这些节点上的c数组代表的值是只有一位的。

而对于最后两位是10的位，也就是c[2]和c[6]，其位于二叉树的倒数第二层，我们约定，这些节点上的c数组所代表的值也是其下面所有叶节点的值之和。可以看出，在这一层的节点控制2个叶节点。

最后三位是100的位，也就是上图的c[4]，其位于二叉树的倒数第三层，这一层的节点控制4个叶节点，c数组同理可以得出。

同样的，最后四位是1000的位，其位于二叉树的倒数第四层，它控制8个叶节点。

 

我们能不能扩展到一般情况呢？

可以。我们假设有一个二进制数m，从最低位向最高位数，如果拥有n个‘0’位，那么这个节点将控制2^n个叶节点，其上的c数组代表的是[m-2^n+1,m]的区间和。

 

那么2^n应该怎么求呢？有一个叫lowbit的东西，它能取得最低位的1表示的数。

那么lowbit的实现方法？

int lowbit(int m){
    return m&(-m);
}

 

可以证明，2^n = m & (-m) （位运算）

 

如果在改动a数组之后，还要花O(n)时间去修改c数组，那么树状数组就没有任何意义了，因为无法得到性能的提升，实际上，树状数组可以在O(logn)的时间内完成一次修改。

因为改动一次a，没有必要去把整个的c数组改动，只需改动一部分即可。

假如我们要改动a[3]，那么显然的，我们要改动的c数组应该是c[3],c[4]和c[8]，因为只有这几个点控制3号叶节点，其他的点不控制3号叶节点所以不受影响。

可以看出，c[3],c[4],c[8]是3号节点的祖先。

 

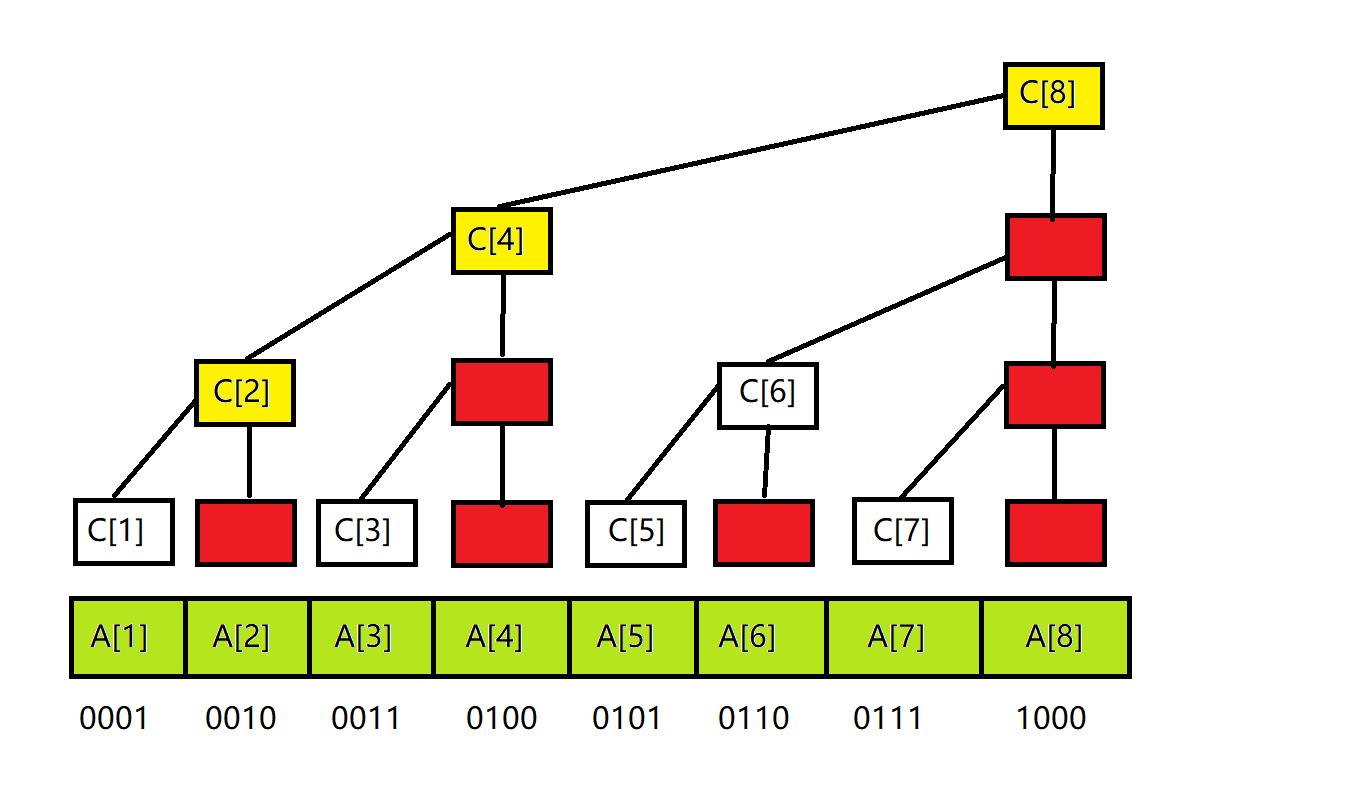
我们推广到一般情况，对于一次修改操作，我们怎样才能得知c数组的变化呢？

由之前二进制位的讨论，我们知道，对于一个点，这个点控制的叶节点大于1，那么这个点应该是某个点的父亲节点。

那么，一般的，如果一个a[i]发生改变，那么其对应的节点c[i]便也会发生改变，c[i]的父亲节点也会发生改变，c[i]的父亲节点的父亲节点也会发生改变……等等

下面是求c[n]的代码：

 　　

int sumele(int n){
    int sum = 0;
    while (n>0){
        sum += c[n];
        n -= lowbit(n);
    }
    return sum;
}

 

更新c[i]的代码：

void update(int i,int val){
    while (i<=n){
        c[i] += val;
        i += lowbit(i);
    }
}

 

 

这样。每次修改只有O(logn)，达到预期的性能要求。

 

附luoguP3374（https://www.luogu.org/problem/show?pid=3374#sub） 树状数组模板题AC代码：

 1 #include <iostream>
 2 #define maxn 500005
 3 using namespace std;
 4 inline int read(){
 5     int num = 0;
 6     char c;
 7     bool flag = false;
 8     while ((c = getchar()) == \' \' || c == \'\\n\' || c == \'\\r\');
 9     if (c == \'-\')
10         flag = true;
11     else
12         num = c - \'0\';
13     while (isdigit(c = getchar()))
14         num = num * 10 + c - \'0\';
15     return (flag ? -1 : 1) * num;
16 }
17 int n,m;
18 int a[maxn],c[maxn];
19 int lowbit(int n){
20     return n&-n;
21 }
22 int sumele(int n){
23     int sum = 0;
24     while (n>0){
25         sum += c[n];
26         n -= lowbit(n);
27     }
28     return sum;
29 }
30 void update(int i,int val){
31     while (i<=n){
32         c[i] += val;
33         i += lowbit(i);
34     }
35 }
36 
37 int main(){
38     n = read();
39     m = read();
40     for (int i=1;i<=n;i++){
41         a[i] = read();
42         update(i,a[i]);
43     }
44     for (int i=1;i<=m;i++){
45         int opnum,x,y;
46         opnum = read();
47         x = read();
48         y = read();
49         if (opnum == 1){
50             update(x,y);
51         }
52         else
53             cout << sumele(y) - sumele(x-1) << endl;
54         
55     }
56     return 0;
57 }