学习笔记-树状数组(21.8.11)

Posted 2021-09-05 未定_

二进制真的牛，以前做比赛训练题的时候经常发现一些大神用二进制角度巧妙问题，自己觉得挺难也没太深入了解，树状数组算是新区域的一次探索。虽然平时习惯了十进制角度想问题，二进制觉得别扭，但学起来发现并没有想象中的那么难，新知识get成功，接下来还需要多训练多总结多消化。关于奇妙的二进制，继续遇到，继续学习。
一、树状数组
常用于处理以下情况：一是修改某元素的值；二是求某段区间的和。
处理问题上比线段树更高效。
二、操作
1.求和运算（区间查询）
•lowbit()操作
lowbit(x)=x&-x，用于找到x的二进制的最后一个1。

补充：•补码:
•正数的补码和原码相同
•负数的补码:将该数的绝对值的二进制形式按位取反再加上1
•&操作：
•1&1=1；0&0=0；0&1=0；1&0=0
即：同1为1，否则为0
•与运算特殊用途：清零、取一个数中指定位详细解释
从lowbit(x)到tree[]数组
令m=lowbit(x)，用tree[x]表示ax和他前面m个数相加，如下图：tree[4]=a1+a2+a3+a4

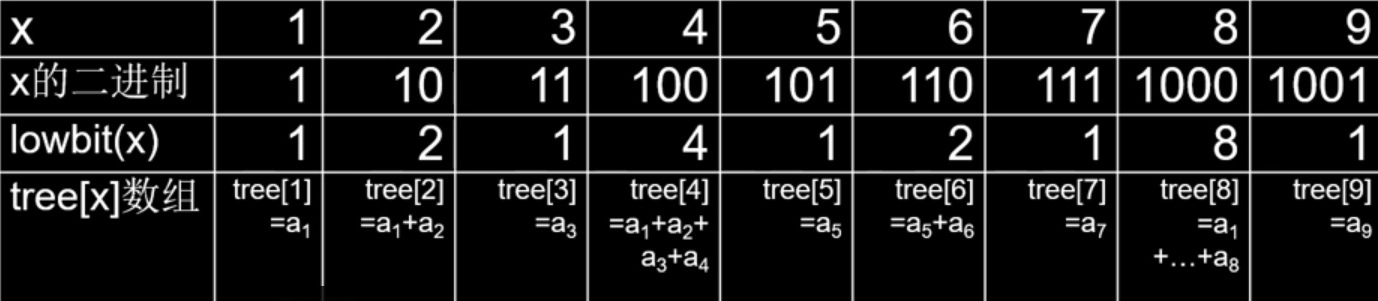
下图中：横线上黑色部分为tree[x]，等于横线上的元素的相加和，类似一棵二叉树

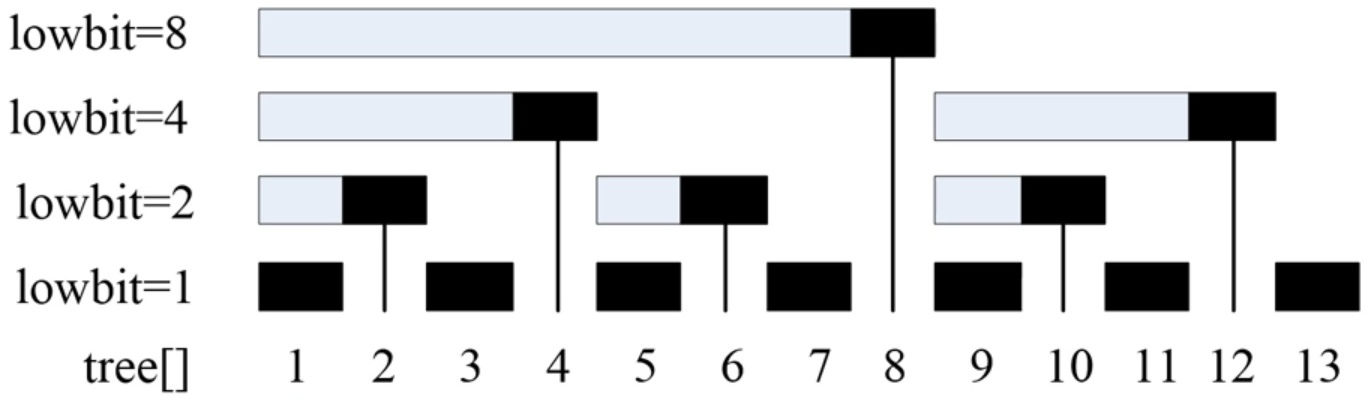
求sum=a1+a2+…+ax，即求tree[x]，从上图可得：sum[7]=tree[7]+tree[6]+tree[4]
原理就是：从7开始加tree[7]，7-lowbit(7)=6所以加上tree[6]，6-lowbit(6)=4再加上tree[4]，4-lowbit[4]=0结束。
换一种理解7的二进制为111，首先加本身tree[7]，右边第一个一变零为110即6，加tree[6]，然后右边第一个一变零100即4，加tree[4]，再右边第一个一变成0结束。

#define lowbit(x) ((x)&-(x))
int sum(int x)
{
    int sum=0;
    while(x>0)
    {   sum+=tree[x];
        x-=lowbit(x);
    }
    return sum;
}

2.修改元素（单点修改）
修改元素ax，与之相关的tree[]都需要改变。
如:修改tree[2]，2+lowbit(2)=4修改tree[4]，4+lowbit(4)=8修改tree[8]…修改tree[n]
另一种理解2的二进制为10，末位为0先修改本身tree[2]，右边补0为100即4，修改tree[4]，继续末位补0；但如果一开始修改的数是3二进制为11，末位为1，先修改本身tree[3]，然后把二进制11加1变成100即4，修改tree[4]，继续末位补0操作。
以下代码：修改的值为d

#define lowbit(x) ((x)&-(x))
void add(int x,int d)
{
    while(x<=n)
    {
        tree[x]+=d;
        x+=lowbit(x);
    }
}

Lost Cows
题意：编号1～n的数字乱序排列，每个位置的数字知道前面比它小的数字个数，求乱序数列。
线段树做法
例子：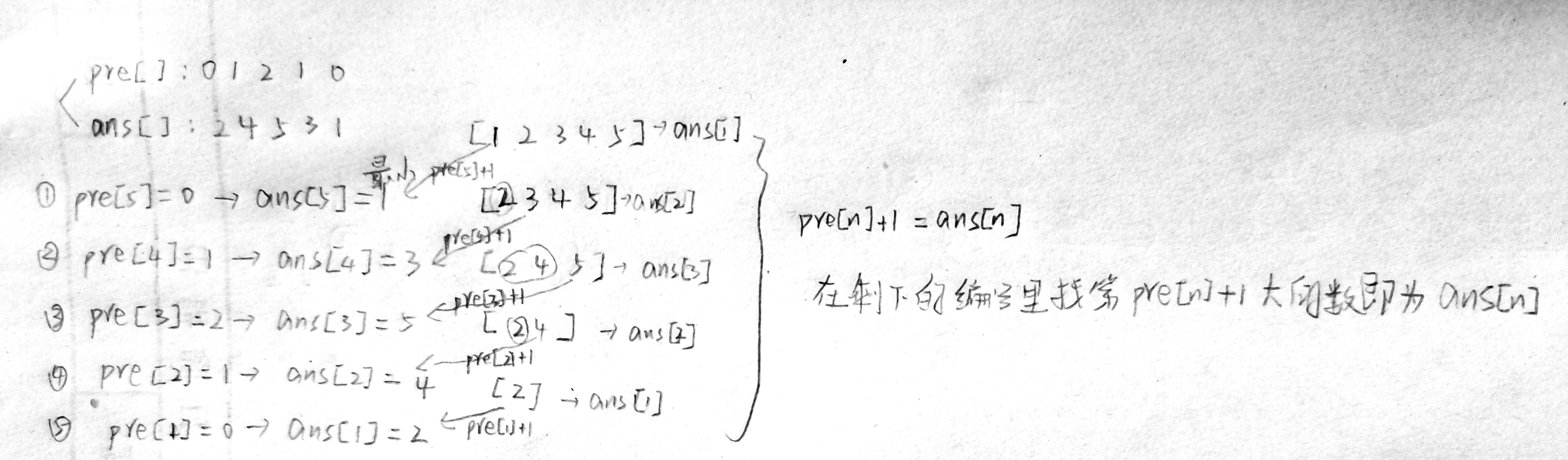
树状数组做法，让pre[i]+1=sum(x)，sum(x)中的x就是上图的ans[n]，也就是第几个数字。
建树，让tree[i]=lowbit(i)，每找到一个数字i，就要把tree[i]及相关tree减1，通过add(x,-1)实现
•为什么用tree[i]=lowbit(i)建树？

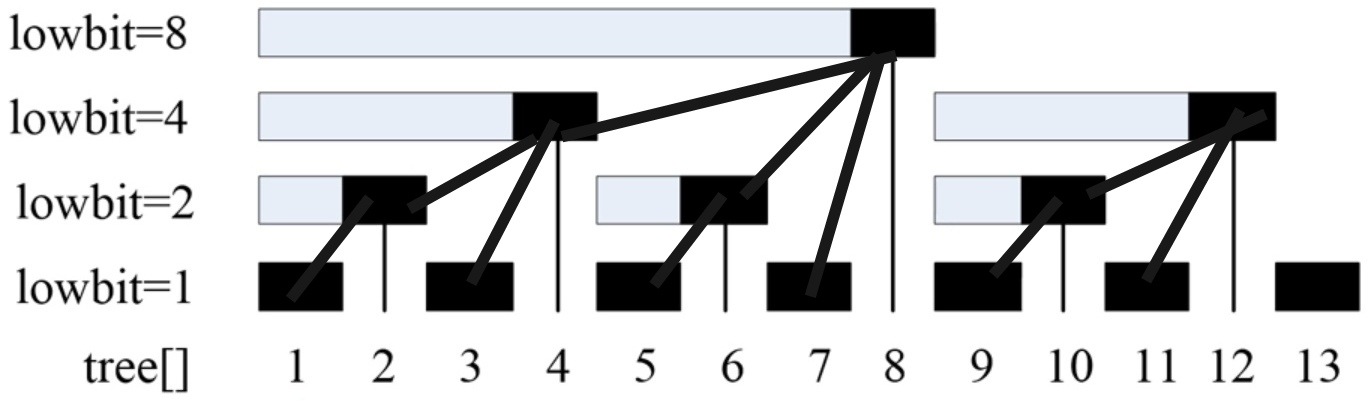
tree[1]=1	sum[1]=tree[1]=1
tree[2]=2	sum[2]=tree[2]=2
tree[3]=1	sum[3]=tree[2]+tree[3]=3
tree[4]=4	sum[4]=tree[4]=4
tree[5]=1	sum[5]=tree[5]+tree[4]=5

发现sum的值就是数列中第几个数字，如果数列不是从1开始，比如2～5

sum[1]=0	tree[1]=0
sum[2]=1	tree[2]=1
sum[3]=tree[2]+tree[3]=2	tree[3]=1
sum[4]=tree[4]=3	tree[4]=3
sum[5]=tree[5]+tree[4]=4	tree[5]=1

与上表相比tree[1]-1；tree[2]-1；tree[4]-1，即add(1，-1)，所以每次找到一个数字x，都要进行add(x，-1)更新tree[]

•怎么找sum(x)中的x？
可以通过二分法搜索x

#include<cstdio>
#include<cstring>
#include<iostream>
#define lowbit(x) ((x)&-(x))
using namespace std;
const int Max = 10000;
int tree[Max], pre[Max], ans[Max];
int n;
void add(int x, int d) {
    while(x <= n) {
        tree[x] += d;
        x += lowbit(x);
    }
}
int sum(int x) {
    int sum = 0;
    while(x > 0) {
        sum += tree[x];
        x -= lowbit(x);
    }
    return sum;
}
int findpos(int x)//寻找sum(x) = pre[i]+1所对应的x
{
    int l = 1, r = n;
    while(l < r) {
        int mid = (l+r) >> 1;
        if(sum(mid) < x)
            l = mid + 1;
        else
            r = mid;
    }
    return l;
}
int main() {
    scanf("%d",&n);
    pre[1] = 0;
    for(int i=2; i <= n; i++)
        scanf("%d",&pre[i]);
    for(int i=1; i <= n; i++)
    {
        tree[i] = lowbit(i);
    }
    for(int i = n; i > 0; i--)
    {
        int x = findpos(pre[i] + 1);
        add(x, -1);  //更新tree数组。
        ans[i] = x;
    }
    for(int i=1; i <= n; i++)
        printf("%d\\n", ans[i]);
    return 0;
}

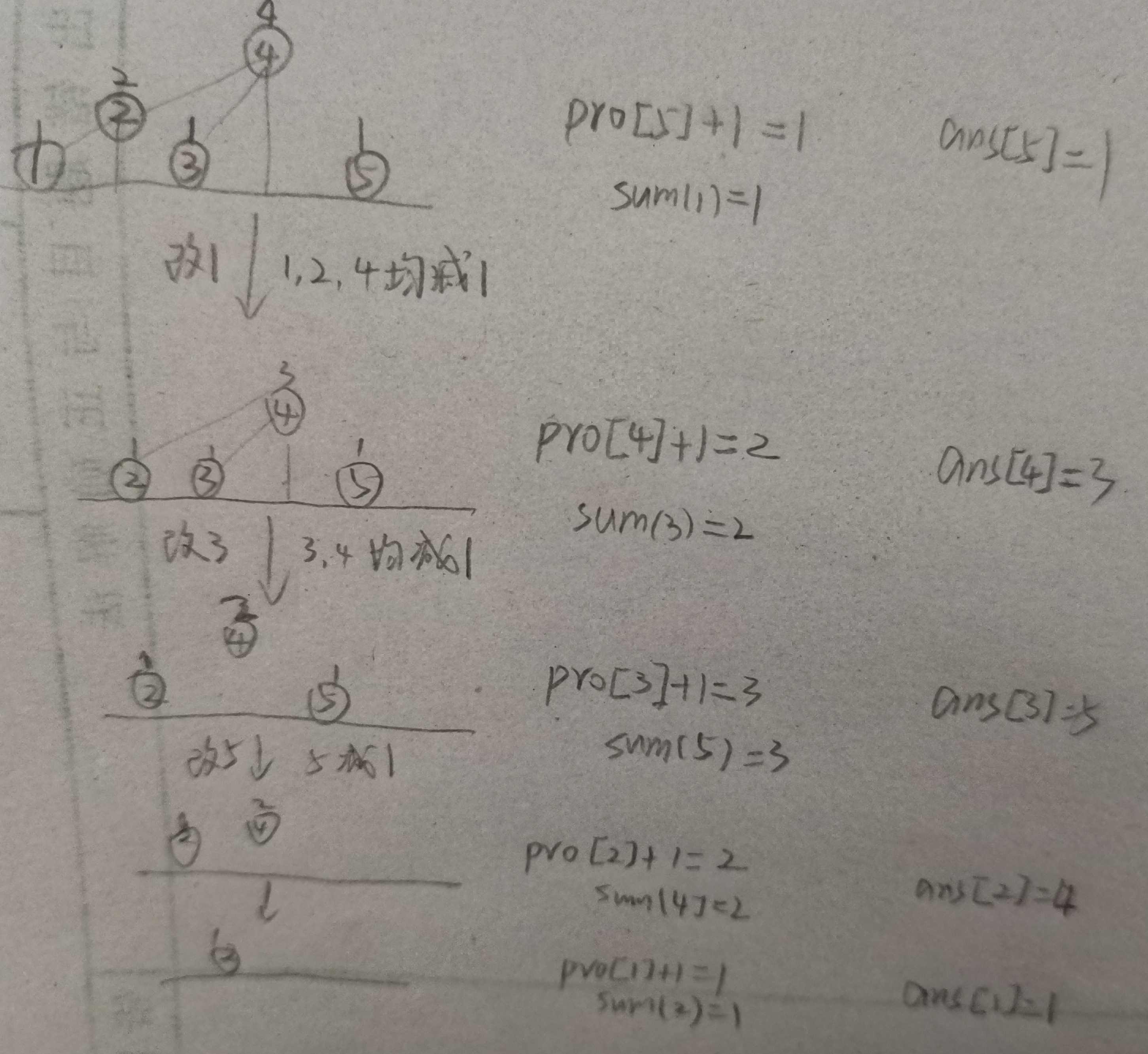
附一张可能没什么用的运行过程图片