HDU 6216 A Cubic number and A Cubic Number（数学/二分查找）

Posted 2020-10-07 Neord

题意：

给定一个素数p（p <= 1e12)，问是否存在一对立方差等于p。

分析：

根据平方差公式：

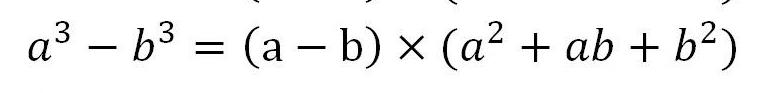
因为p是一个素数， 所以只能拆分成 1*p， 所以 a-b = 1.

然后代入a = b + 1. 求出 3a² + 3a + 1 = p

化简得a(a+1) = (p-1)/3

令(p-1)/3 = T， 问题化为是否存在整数a使得a(a+1) == T， 那么令 t = (int)sqrt(T)，只要判定一下t * （t+1） == T ? 即可

 

另一种做法是打一个a的表（a只要打到1e6）， 然后二分查找是否， 主要锻炼一下二分查找的代码实现。

（这题在网络赛时候我是打表找出规律的， 发现符合的数一定是形如1 + 6*（1+2+3...+k）这样的， 以后碰到这种题可以先打表看看有无规律）

代码：

数学方法：

#include <bits/stdc++.h>
using namespace std;
int main(){
    int T;
    scanf("%d", &T);
    while(T--){
        double p;
        scanf("%lf", &p);
        double T = (p-1.0)/3;
        double a = floor(sqrt(T));
        if(a*(a+1) == T)
            printf("YES\\n");
        else printf("NO\\n");
    }
    return 0;
}

二分查找：

#include <iostream>
#include <cstdio>
#include <string>
#include <algorithm>
#define ll long long

using namespace std;

const int MAXN = 1e6 + 5;
ll tab[MAXN];

void init()
{
    for (int i = 0;i < MAXN;++i)
        tab[i] = 3LL * i*i + 3 * i + 1;
}

int main()
{
    init();
    int T;
    scanf("%d", &T);
    while(T--){
        long long p;
        scanf("%lld", &p);
        int left = 0, right = MAXN - 1;
        int mid = (left+right) >> 1;
        int flag = 0;
        while(left <= right){
            if(p == tab[mid]){
                flag = 1;
                break;
            }
            else if(p > tab[mid]){
                left = mid + 1;
            }
            else right = mid - 1;
            mid = (left+right) >> 1;
        }
        if(flag)
            printf("YES\\n");
        else printf("NO\\n");
    }
    return 0;
}