[ZJOI 2012]灾难

Posted 2020-09-30 NaVi_Awson

Description

阿米巴是小强的好朋友。

阿米巴和小强在草原上捉蚂蚱。小强突然想，果蚂蚱被他们捉灭绝了，那么吃蚂蚱的小鸟就会饿死，而捕食小鸟的猛禽也会跟着灭绝，从而引发一系列的生态灾难。

学过生物的阿米巴告诉小强，草原是一个极其稳定的生态系统。如果蚂蚱灭绝了，小鸟照样可以吃别的虫子，所以一个物种的灭绝并不一定会引发重大的灾难。

我们现在从专业一点的角度来看这个问题。我们用一种叫做食物网的有向图来描述生物之间的关系：

一个食物网有N个点，代表N种生物，如果生物x可以吃生物y，那么从y向x连一个有向边。

这个图没有环。

图中有一些点没有连出边，这些点代表的生物都是生产者，可以通过光合作用来生存； 而有连出边的点代表的都是消费者，它们必须通过吃其他生物来生存。

如果某个消费者的所有食物都灭绝了，它会跟着灭绝。

我们定义一个生物在食物网中的“灾难值”为，如果它突然灭绝，那么会跟着一起灭绝的生物的种数。

举个例子：在一个草场上，生物之间的关系是：

如果小强和阿米巴把草原上所有的羊都给吓死了，那么狼会因为没有食物而灭绝，而小强和阿米巴可以通过吃牛、牛可以通过吃草来生存下去。所以，羊的灾难值是1。但是，如果草突然灭绝，那么整个草原上的5种生物都无法幸免，所以，草的灾难值是4。

给定一个食物网，你要求出每个生物的灾难值。

Input

输入文件 catas.in 的第一行是一个正整数 N，表示生物的种数。生物从 1 标号到 N。

接下来 N 行，每行描述了一个生物可以吃的其他生物的列表，格式为用空格隔开的若干个数字，每个数字表示一种生物的标号，最后一个数字是 0 表示列表的结束。

Output

输出文件catas.out包含N行，每行一个整数，表示每个生物的灾难值。

Sample Input

5
0
1 0
1 0
2 3 0
2 0

Sample Output

4
1
0
0
0

Hint

【样例说明】

样例输入描述了题目描述中举的例子。

【数据规模】

对50%的数据，N ≤ 10000。

对100%的数据，1 ≤ N ≤ 65534。

输入文件的大小不超过1M。保证输入的食物网没有环。

题解

拓扑排序+倍增$LCA$

暴力的n²算法肯定是不行的，我们需要考虑特殊的做法。

由于每次有且只有一种生物灭绝，而当且仅当x的所有食物都灭绝，$x$才会灭绝。

所以所有$x$的食物从上至下能共同达到的某个节点灭绝时，$x$才会灭绝。

根据这个我们可以重构树然后跑$LCA$。

先把所有没有食物的点（题目中描述为“生产者”）向$0$连一条边。

然后对原图进行拓扑排序，得到每个点进队列的顺序。

再从后向前扫一遍，对于每个点，对它的所有食物节点求一下$LCA$（两两求一次），将这个点连到$LCA$上。

由于我们加了“生产者”$->0$的一条边，所以能够使得加进来的是一棵树，而不是一个森林。

每次重构时，不需要$LCT$，直接看作新加一个节点$x$，$f[x][0]=LCA$，然后处理一下就行了。

最后要求的就是子树大小$-1$，所以利用拓扑排序（也就是一种$bfs$序）向上更新即可。

举样例的例子：

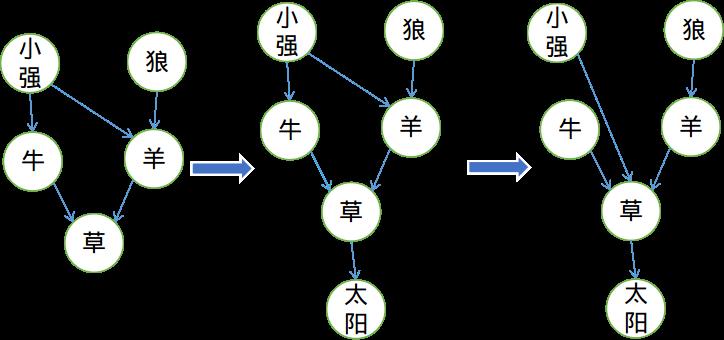
我们容易发现草的灾难值为$4$，羊的灾难值为$1$。

$Ps$：听说这东西叫灭绝树，还以为是什么奇怪的数据结构，就是拓扑排序+倍增$LCA$。估计这就是母题了吧？

神犇的注解：

    我们需要构造一棵“灭绝树”。
    “灭绝树”满足以下性质：对于一棵多叉树的任意一个结点，当它“灭绝”时，它所有的后代也会跟着“灭绝”。
    再回过来看这道题，题目要求的是某种生物“灭绝”后跟着“灭绝”的其他生物的数量，即这种生物在“灭绝树”中的后代数量。
    那么问题来了，怎么建立“灭绝树”？
    很显然，一种生物会“灭绝”只有两种情况：一是它原本就“灭绝”（即我们要求灾难值的那种生物），二是它所有的食物都“灭绝”。
    第一种情况不用考虑，那么我们来考虑第二种情况。
    假设有生物I。很显然，只有当生物I的所有食物的最近公共祖先（LCA）J“灭绝”时，生物I的所有食物才会同时“灭绝”（显然这里就要用到倍增求LCA的算法），然后，我们将生物I作为生物J的一个新的孩子节点，表示当J“灭绝”时，I也会跟着“灭绝”（因为它所有的食物都“灭绝”了）。
    根据题目需求，最后只要输出每种生物在“灭绝树”中的所有后代数量（数量的计算可以在每次“灭绝树”加入新节点时进行一次DFS）就可以了。

 1 #include<map>
 2 #include<ctime>
 3 #include<cmath>
 4 #include<queue>
 5 #include<stack>
 6 #include<cstdio>
 7 #include<string>
 8 #include<vector>
 9 #include<cstring>
10 #include<cstdlib>
11 #include<iostream>
12 #include<algorithm>
13 #define LL long long
14 #define RE register
15 #define IL inline
16 using namespace std;
17 const int N=65534;
18 const int M=1000000;
19 
20 int n,x,op;
21 struct tt
22 {
23     int to,next;
24 }edge[M+5];
25 int path[N+5],top;
26 IL void Add(int u,int v);
27 
28 int in[N+5];
29 int size[N+5];
30 
31 int q[N+5],head,tail;
32 IL void Topsort();
33 
34 int deep[N+5],fa[N+5][20];
35 IL int LCA(int x,int y);
36 
37 int main()
38 {
39     scanf("%d",&n);
40     op=log2(n);
41     for (RE int i=1;i<=n;i++)
42     {
43         scanf("%d",&x);
44         if (!x) Add(i,0);
45         while (x)
46         {
47             Add(i,x);
48             in[x]++;
49             scanf("%d",&x);
50         }
51     }
52     Topsort();
53     for (RE int i=n;i>=1;i--)
54     {
55         int u=q[i],t=edge[path[u]].to;
56         for (RE int j=edge[path[u]].next;j;j=edge[j].next) t=LCA(t,edge[j].to);
57         fa[u][0]=t;
58         deep[u]=deep[t]+1;
59         for (RE int t=1;t<=op;t++) fa[u][t]=fa[fa[u][t-1]][t-1];
60     }
61     for (RE int i=1;i<=n;i++) size[q[i]]++,size[fa[q[i]][0]]+=size[q[i]];
62     for (RE int i=1;i<=n;i++) printf("%d\\n",size[i]-1);
63     return 0;
64 }
65 
66 IL void Topsort()
67 {
68     head=tail=1;
69     for (RE int i=1;i<=n;i++) if (!in[i]) q[tail++]=i;
70     while (head<tail)
71     {
72         int u=q[head++];
73         for (RE int i=path[u];i;i=edge[i].next)
74         {
75             in[edge[i].to]--;
76             if (!in[edge[i].to]) q[tail++]=edge[i].to;
77         }
78     }
79 }
80 IL void Add(int u,int v)
81 {
82     edge[++top].to=v;
83     edge[top].next=path[u];
84     path[u]=top;
85 }
86 IL int LCA(int x,int y)
87 {
88     if (deep[x]<deep[y]) swap(x,y);
89     for (RE int i=op;i>=0;i--) if (deep[fa[x][i]]>=deep[y]) x=fa[x][i];
90     if (x==y) return x;
91     for (RE int i=op;i>=0;i--) if (fa[x][i]!=fa[y][i]) x=fa[x][i],y=fa[y][i];
92     return fa[x][0];
93 }