prufer数列

Posted 2020-09-17 小时のblog

涨姿势---prufer数列

一、

简介

Prufer数列是无根树的一种数列。在组合数学中，Prufer数列由有一个对于顶点标过号的树转化来的数列，点数为n的树转化来的Prufer数列长度为n-2。它可以通过简单的迭代方法计算出来。它由Heinz Prufer于1918年在证明cayley定理时首次提出。

二、

（1）将树转换为prufer数列的方法。

总体的思路是迭代删点，直到原图中只剩下两个点。对于一棵树T,我们已经将每次找到树中标号最小的叶子结点，将这个叶子结点以及与它相邻的边删去，将与叶子结点相连

的点加入数列中。重复上一步，直到原图中只剩下两个点。

例子：以右边的树为例子，首先在所有叶子节点中编号最小的点是2，和它相邻的点的编号是3，将3加入序列并删除编号为2的点。接下来删除的点是4，5被加入序列，然后删除5，1，此时原图仅剩两个点，Prufer序列构建完成，为{3,5,1,3}

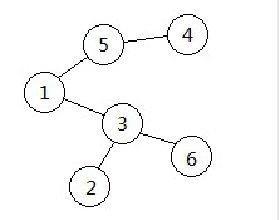
（2）将prufer数列转换为树的方法。

例子：将结点列一个集合A={1，2，3......,n};在集合A中找出一个没有在prufer数列中出现的最小的值，将这个值在集合A中删去，并且将这个值和prufer数列中的第一个数连起一条边，并划去prufer数列中的第一个值，重复此步，直到集合A中只剩下两个数字，将以这两个数字为编号的结点连起一条边。

仍为上面的树，Prufer序列为{3,5,1,3}，开始时G={1,2,3,4,5,6}，未出现的编号最小的点是2，将2和3连边，并删去Prufer序列首项和G中的2。接下来连的边为{4,5},{1,5},{1,3},此时集合G中仅剩3和6，在3和6之间连边，原树恢复。

三、

总结：

可见无根树和prufer数列是唯一对应的。一棵n个节点的无根树唯一地对应了一个长度为n-2的数列，数列中的每个数都在1到n的范围内。

无根树的表示法用prufer数列。

这个数列的特点：

这个点的度数-1=它在数列的出现次数。

prufer序列中某个编号出现的次数+1就等于这个编号的节点在无根树中的度数。

所以数列总长度是n-2。

四、

再看看Cayley公式：

Cayley公式是说，一个完全图K_n有n^(n-2)棵生成树，换句话说n个节点的带标

号的无根树有n^(n-2)个。

五、

附赠prufer数列裸题三套：（不用谢ovo）

bzoj 1211

bzoj 1430

bzoj 1005