平衡二叉树的问题！

Posted 2023-04-18

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了平衡二叉树的问题！相关的知识，希望对你有一定的参考价值。

如题：画出以序列25,27,30,12,11,18,14,20,15,22，我想问的是，当做这道题的时候，是先按一个个节点的插入构造二叉排序树，然后统一进行平衡模式的转换，还是一个个节点的插入，一不平衡就调整呢？这两种方法的话，答案肯定不一样。在线等待！

参考技术A 1.平衡二叉树解决的是动态问题，静态的查找无需平衡树，一般排序+二分或线段树即可。
2.平衡树的样子不重要，它只是解题过程中用到的一个工具，只要符合平衡树的条件怎么个顺序就无所谓。本回答被提问者采纳参考技术B 这个问题的中文意思是:
“任何一个平衡二叉树，如果它总共有16个结点，那么它的*最大*深度是多少?”
解答:(我用星号表示结点)平衡二叉树是这样的二叉树:它的左右子树都是平衡二叉树，且两者深度之差不超过1
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
(图1
每个父结点度有左右两个子结点)
答案:a 参考技术C 通常采用：一个个节点插入，一部平衡就调整！参考技术D

平衡二叉树（AVL）

那对图 1 进行下改造，把数据重新节点重新连接下，图 2 如下：

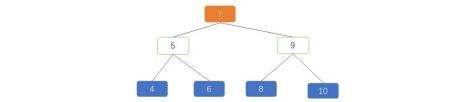
图 2 可以看到以下特性：

1. 所有左子树的节点都小于其对应的父节点（4，5，6）<（7）；（4）<（5）；（8）< （9）；

2. 所有右子树上的节点都大于其对应的父节点（8，9，10）>（7）；（6）>（5）；（10）>（9）；

3. 每个节点的平衡因子差值绝对值 <=1；

4. 每个节点都符合以上三个特征。

满足这样条件的树叫平衡二叉树（AVL）树。

问：那再次查找节点 5，需要遍历多少次呢？

由于数据是按照顺序组织的，那查找起来非常快，从上往下找：7-5，只需要在左子树上查找，也就是遍历 2 次就找到了 5。假设要找到叶子节点 10，只需要在右子树上查找，那也最多需要 3 次，7-9-10。也就说 AVL 树在查找方面性能很好，最坏的情况是找到一个节点需要消耗的次数也就是树的层数，复杂度为 O(logN)

如果节点非常多呢？假设现在有 31 个节点，用 AVL 树表示如图 3：

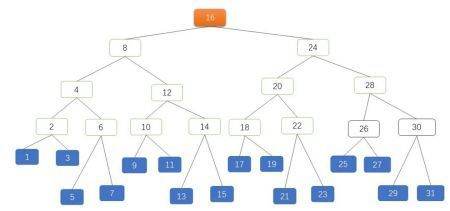
图 3 是一棵高度为 4 的 AVL 树，有 5 层共 31 个节点，橙色是 ROOT 节点，蓝色是叶子节点。对 AVL 树的查找来看起来已经很完美了，能不能再优化下？比如，能否把这个节点里存放的 KEY 增加？能否减少树的总层数？那减少纵深只能从横向来想办法，这时候可以考虑用多叉树。

树结构系列：平衡二叉树AVL树红黑树

前面说到二叉树在极端情况下会退化成链表，那如何解决这个问题呢？

答案是：树的平衡。我们通过树的平衡，使得左右子树的深度保持在较小范围内，从而保证二叉树的查询效率。这就是平衡二叉树的核心思想。这种能平衡左右子树的二叉树，我们称之为平衡二叉树。

官方对于平衡树的定义是：任意节点的子树的高度差都小于等于 1。常见的符合平衡树的有：2-3 树、B 树、AVL 树等。红黑树是一种特殊的自平衡树，其子树的高度差并不一定小于等于 1。AVL 树虽然查询效率高，但是插入、删除效率低，需要不断旋转以保持平衡。而红黑树通过牺牲一些查询效率，提高了插入、删除的效率。

AVL树

AVL 树是最早发明的自平衡二叉查找树。在 AVL 树中任何节点的两个子树的高度最大差别为 1，所以它也被称为高度平衡树。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。AVL 树得名于它的发明者 G. M. Adelson-Velsky 和 E. M. Landis，他们在 1962 年的论文《An algorithm for the organization of information》中发表了它。

AVL 树本质上还是一棵二叉搜索树，但是其比二叉搜索树还多了平衡功能。它的特点是：

本身首先是一棵二叉搜索树。
带有平衡条件：每个结点的左右子树的高度之差的绝对值（平衡因子）最多为 1。

也就是说，AVL 树本质上是带了平衡功能的二叉搜索树。

AVL 树的旋转操作，本质上和红黑树的类似，这里就不细讲。我们在下面讲解红黑树的时候再展开说。

红黑树

红黑树（Red Black Tree）是一种自平衡二叉查找树，是在计算机科学中用到的一种数据结构。红黑树是在 1972 年由 Rudolf Bayer 发明的，当时被称为平衡二叉 B 树（symmetric binary B-trees）。后来，在 1978 年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的「红黑树」。

红黑树是一种特化的 AVL 树（平衡二叉树），都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡，从而获得较高的查找性能。

它虽然是复杂的，但它的最坏情况运行时间也是非常良好的，并且在实践中是高效的：它可以在 O (log N) 时间内做查找、插入和删除，这里的 N 是树中元素的数目。

对于红黑树来说，其可能有如下一些特点：

若一棵二叉查找树是红黑树，则它的任一子树必为红黑树。
红黑树是一种平衡二叉查找树的变体，它的左右子树高差有可能大于 1。
与 AVL 树相比，其通过牺牲查询效率来提升插入、删除效率。

红黑树是在二叉查找树的基础上演化进来的，除了二叉查找树的要求之外，红黑树还具有如下五个强制要求（属性）：

性质 1. 结点是红色或黑色。
性质 2. 根结点是黑色。
性质 3. 所有叶子都是黑色。（叶子是 NIL 结点）。
性质 4. 每个红色结点的两个子结点都是黑色。（从每个叶子到根的所有路径上不能有两个连续的红色结点）。
性质 5. 任意一节点到每个叶子节点的路径都包含数量相同的黑节点。

上面这 5 个性质使得红黑树有一个关键的性质：从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是这个树大致上是平衡的。为何会有这样一个结果，其实从性质中我们就可以大概猜出一二。

性质 4 与性质 5 是红黑树关键的核心性质。性质 4 表明一个节点到根节点的最短可能路径都是黑色节点，最长可能路径有交替红色和黑色节点。根据性质 5 所有最长的路径都有相同数目的黑色结点，这就表明了没有路径能多于任何其他路径的两倍长。

当我们在对红黑树进行插入和删除等操作时，对树做了修改，那么可能会违背红黑树的性质。为了保持红黑树的性质，我们可以对相关结点做一系列的调整，通过对树进行旋转（例如左旋和右旋操作），即修改树中某些结点的颜色及指针结构，以达到对红黑树进行插入、删除结点等操作时，红黑树依然能保持它特有的五个性质。

红黑树操作

红黑树的基本操作和其他树形结构一样，一般都包括查找、插入、删除等操作。前面说到，红黑树是一种自平衡的二叉查找树，既然是二叉查找树的一种，那么查找过程和二叉查找树一样，比较简单，这里不再赘述。相对于查找操作，红黑树的插入和删除操作就要复杂的多。

尤其是删除操作，要处理的情况比较多，不过大家如果静下心来去看，会发现其实也没想的那么难。好了，废话就说到这，接下来步入正题吧。

旋转操作

在分析插入和删除操作前，这里需要插个队，先说明一下旋转操作，这个操作在后续操作中都会用得到。旋转操作分为左旋和右旋，左旋是将某个节点旋转为其右孩子的左孩子，而右旋是节点旋转为其左孩子的右孩子。这话听起来有点绕，所以还是请看下图：

上图包含了左旋和右旋的示意图，这里以右旋为例进行说明，右旋节点 M 的步骤如下：

将节点 M 的左孩子引用指向节点 E 的右孩子
将节点 E 的右孩子引用指向节点 M，完成旋转

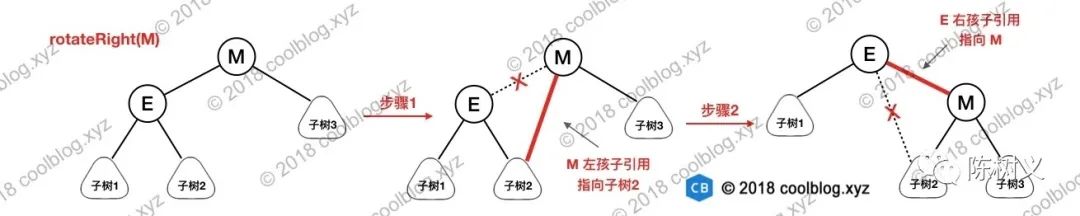
上面分析了右旋操作，左旋操作与此类似，大家有兴趣自己画图试试吧，这里不再赘述了。旋转操作本身并不复杂，这里先分析到这吧。

插入操作

红黑树的插入过程和二叉查找树插入过程基本类似，不同的地方在于，红黑树插入新节点后，需要进行调整，以满足红黑树的性质。性质 1 规定红黑树节点的颜色要么是红色要么是黑色，那么在插入新节点时，这个节点应该是红色还是黑色呢？

答案是红色，原因也不难理解。如果插入的节点是黑色，那么这个节点所在路径比其他路径多出一个黑色节点，这个调整起来会比较麻烦（参考红黑树的删除操作，就知道为啥多一个或少一个黑色节点时，调整起来这么麻烦了）。

如果插入的节点是红色，此时所有路径上的黑色节点数量不变，仅可能会出现两个连续的红色节点的情况。这种情况下，通过变色和旋转进行调整即可，比之前的简单多了。

接下来，将分析插入红色节点后红黑树的情况。这里假设要插入的节点为 N，N 的父节点为 P，祖父节点为 G，叔叔节点为 U。插入红色节点后，会出现 5 种情况，分别如下：

情况一

插入的新节点 N 是红黑树的根节点，这种情况下，我们把节点 N 的颜色由红色变为黑色，性质 2（根是黑色）被满足。同时 N 被染成黑色后，红黑树所有路径上的黑色节点数量增加一个，性质 5（从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点）仍然被满足。

情况二

N 的父节点是黑色，这种情况下，性质 4（每个红色节点必须有两个黑色的子节点）和性质 5 没有受到影响，不需要调整。

情况三

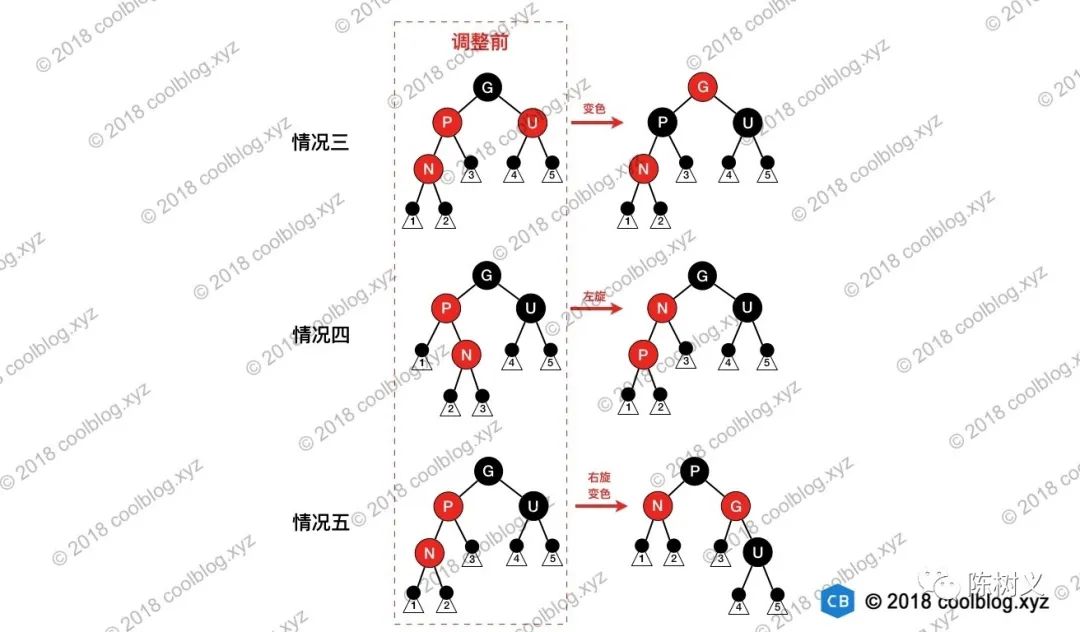
N 的父节点是红色（节点 P 为红色，其父节点必然为黑色），叔叔节点 U 也是红色。由于 P 和 N 均为红色，所有性质 4 被打破，此时需要进行调整。这种情况下，先将 P 和 U 的颜色染成黑色，再将 G 的颜色染成红色。

此时经过 G 的路径上的黑色节点数量不变，性质 5 仍然满足。但需要注意的是 G 被染成红色后，可能会和它的父节点形成连续的红色节点，此时需要递归向上调整。

情况四

N 的父节点为红色，叔叔节点为黑色。节点 N 是 P 的右孩子，且节点 P 是 G 的左孩子。此时先对节点 P 进行左旋，调整 N 与 P 的位置。接下来按照情况五进行处理，以恢复性质 4。

情况五

N 的父节点为红色，叔叔节点为黑色。N 是 P 的左孩子，且节点 P 是 G 的左孩子。此时对 G 进行右旋，调整 P 和 G 的位置，并互换颜色。经过这样的调整后，性质 4 被恢复，同时也未破坏性质 5。

插入总结

上面五种情况中，情况一和情况二比较简单，情况三、四、五稍复杂。但如果细心观察，会发现这三种情况的区别在于叔叔节点的颜色，如果叔叔节点为红色，直接变色即可。如果叔叔节点为黑色，则需要选选择，再交换颜色。当把这三种情况的图画在一起就区别就比较容易观察了，如下图：

删除操作

相较于插入操作，红黑树的删除操作则要更为复杂一些。删除操作首先要确定待删除节点有几个孩子，如果有两个孩子，不能直接删除该节点。而是要先找到该节点的前驱（该节点左子树中最大的节点）或者后继（该节点右子树中最小的节点），然后将前驱或者后继的值复制到要删除的节点中，最后再将前驱或后继删除。

由于前驱和后继至多只有一个孩子节点，这样我们就把原来要删除的节点有两个孩子的问题转化为只有一个孩子节点的问题，问题被简化了一些。我们并不关心最终被删除的节点是否是我们开始想要删除的那个节点，只要节点里的值最终被删除就行了，至于树结构如何变化，这个并不重要。

红黑树删除操作的复杂度在于删除节点的颜色，当删除的节点是红色时，直接拿其孩子节点补空位即可。因为删除红色节点，性质 5（从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点）仍能够被满足。当删除的节点是黑色时，那么所有经过该节点的路径上的黑节点数量少了一个，破坏了性质 5。

如果该节点的孩子为红色，直接拿孩子节点替换被删除的节点，并将孩子节点染成黑色，即可恢复性质 5。但如果孩子节点为黑色，处理起来就要复杂的多。分为 6 种情况，下面会展开说明。

在展开说明之前，我们先做一些假设，方便说明。这里假设最终被删除的节点为 X（至多只有一个孩子节点），其孩子节点为 N，X 的兄弟节点为 S，S 的左节点为 SL，右节点为 SR。接下来讨论是建立在节点 X 被删除，节点 N 替换 X 的基础上进行的。这里说明把被删除的节点 X 特地拎出来说一下的原因是防止大家误以为节点 N 会被删除，不然后面就会看不明白。

在上面的基础上，接下来就可以展开讨论了。红黑树删除有 6 种情况，分别是：

情况一

N 是新的根。在这种情形下，我们就做完了。我们从所有路径去除了一个黑色节点，而新根是黑色的，所以性质都保持着。

上面是维基百科中关于红黑树删除的情况一说明，由于没有配图，看的有点晕。经过思考，我觉得可能会是下面这种情形：

要删除的节点 X 是根节点，且左右孩子节点均为空节点，此时将节点 X 用空节点替换完成删除操作。

可能还有其他情形，大家如果知道，烦请告知。

情况二

S 为红色，其他节点为黑色。这种情况下可以对 N 的父节点进行左旋操作，然后互换 P 与 S 颜色。但这并未结束，经过节点 P 和 N 的路径删除前有 3 个黑色节点（P -> X -> N），现在只剩两个了（P -> N）。比未经过 N 的路径少一个黑色节点，性质 5 仍不满足，还需要继续调整。不过此时可以按照情况四、五、六进行调整。

情况三

N 的父节点，兄弟节点 S 和 S 的孩子节点均为黑色。这种情况下可以简单的把 S 染成红色，所有经过 S 的路径比之前少了一个黑色节点，这样经过 N 的路径和经过 S 的路径黑色节点数量一致了。但经过 P 的路径比不经过 P 的路径少一个黑色节点，此时需要从情况一开始对 P 进行平衡处理。

情况四

这里需要特别说明一下，上图中的节点 N 并非是新插入的节点。当 P 为红色时，P 有两个孩子节点，且孩子节点均为黑色，这样从 G 出发到各叶子节点路径上的黑色节点数量才能保持一致。既然 P 已经有两个孩子了，所以 N 不是新插入的节点。情况四是由以 N 为根节点的子树中插入了新节点，经过调整后，导致 N 被变为红色，进而导致了情况四的出现。考虑下面这种情况（PR 节点就是上图的 N 节点）：

如上图，插入节点 N 并按情况三处理。此时 PR 被染成了红色，与 P 节点形成了连续的红色节点，这个时候就需按情况四再次进行调整。

情况五

S 为黑色，S 的左孩子为红色，右孩子为黑色。N 的父节点颜色可红可黑，且 N 是 P 左孩子。这种情况下对 S 进行右旋操作，并互换 S 和 SL 的颜色。此时，所有路径上的黑色数量仍然相等，N 兄弟节点的由 S 变为了 SL，而 SL 的右孩子变为红色。接下来我们到情况六继续分析。

情况六

S 为黑色，S 的右孩子为红色。N 的父节点颜色可红可黑，且 N 是其父节点左孩子。这种情况下，我们对 P 进行左旋操作，并互换 P 和 S 的颜色，并将 SR 变为黑色。因为 P 变为黑色，所以经过 N 的路径多了一个黑色节点，经过 N 的路径上的黑色节点与删除前的数量一致。对于不经过 N 的路径，则有以下两种情况：

该路径经过 N 新的兄弟节点 SL ，那它之前必然经过 S 和 P。而 S 和 P 现在只是交换颜色，对于经过 SL 的路径不影响。
该路径经过 N 新的叔叔节点 SR，那它之前必然经过 P、 S 和 SR，而现在它只经过 S 和 SR。在对 P 进行左旋，并与 S 换色后，经过 SR 的路径少了一个黑色节点，性质 5 被打破。另外，由于 S 的颜色可红可黑，如果 S 是红色的话，会与 SR 形成连续的红色节点，打破性质 4（每个红色节点必须有两个黑色的子节点）。此时仅需将 SR 由红色变为黑色即可同时恢复性质 4 和性质 5（从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点）。

删除总结

红黑树删除的情况比较多，大家刚开始看的时候可能会比较晕。可能会产生这样的疑问，为啥红黑树会有这种删除情况，为啥又会有另一种情况，它们之间有什么联系和区别？和大家一样，我刚开始看的时候也有这样的困惑，直到我把所有情况对应的图形画在一起时，拨云见日，一切都明了了。此时天空中出现了 4 个字，原来如此、原来如此、原来如此。所以，请看图吧：

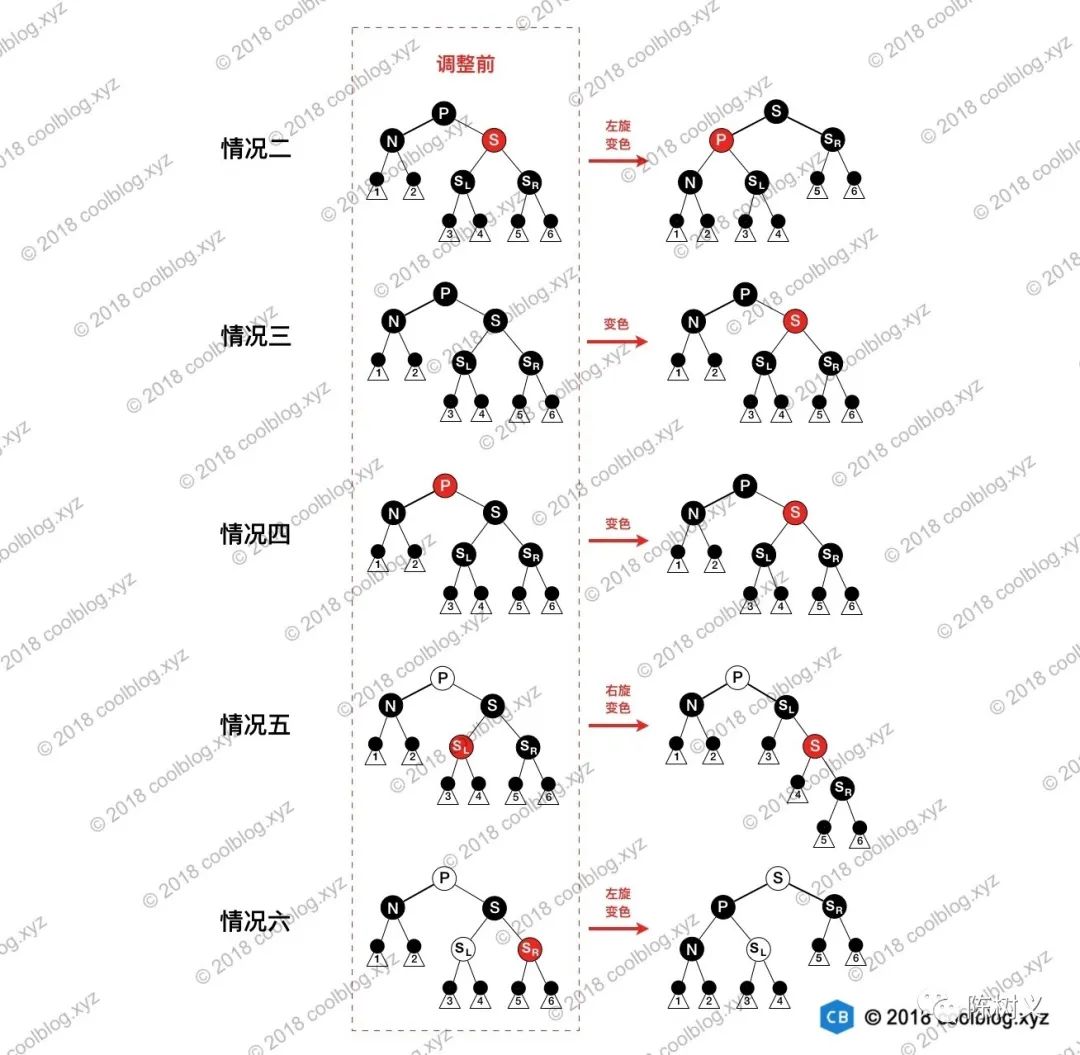
总结

通过平衡二叉树的旋转调整，我们解决了二叉搜索树退化成链表的问题。平衡二叉树是任意节点的子树的高度差都小于等于 1 的二叉搜索树，其最早最典型的应用就是 AVL 树。

虽然 AVL 解决了平衡的问题，但 AVL 树存在插入、删除慢的特点。为了解决该问题，红黑树应运而生。其通过牺牲部分查询效率，提升了插入、删除效率，使其在最坏情况下也能实现 O (log N) 的时间复杂度。接着我们深入介绍了红黑树的旋转操纵，揭示了红黑树是如何实现平衡操作的。

说到这里，红黑树应该说已经是查找、搜索的极限了。但事实上红黑树也有其局限性，即在空间存储方面的局限性。假设我们现在也在 10 亿个数字里面查找某个数，那么我们应该怎么办？

一种最简单的办法就是直接把 10 亿个数加载到内存中，然后在内存中去比较他们的大小。这看着没问题，但实际上内存能装得下 10 亿个数字么？如果装不下，那么我们应该怎么解决这个问题？

上面这个例子的典型应用场景就是我们的数据库索引。对于数据库来说，一个表几十亿的数据是非常正常的。在这种情况下，B 树应运而生，其就是用来解决海量数据的搜索难题的。

下篇文章，我们就来讲讲 B 树是如何解决海量数据的搜索问题。

参考资料

平衡树_百度百科
AVL 树_百度百科
红黑树_百度百科
红黑树详细分析 | 田小波的技术博客