什么是平衡二叉树
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了什么是平衡二叉树相关的知识,希望对你有一定的参考价值。
平衡二叉树,又称AVL树。它或者是一棵空树,或者是具有下列性质的二叉树:它的左子树和右子树都是平衡二叉树,且左子树和右子树的高度之差之差的绝对值不超过1.。常用算法有:红黑树、AVL树、Treap等。
平衡二叉树的调整方法
平衡二叉树是在构造二叉排序树的过程中,每当插入一个新结点时,首先检查是否因插入新结点而破坏了二叉排序树的平衡性,若是,则找出其中的最小不平衡子树,在保持二叉排序树特性的前提下,调整最小不平衡子树中各结点之间的链接关系,进行相应的旋转,使之成为新的平衡子树。具体步骤如下:
⑴ 每当插入一个新结点,从该结点开始向上计算各结点的平衡因子,即计算该结点的祖先结点的平衡因子,若该结点的祖先结点的平衡因子的绝对值均不超过1,则平衡二叉树没有失去平衡,继续插入结点;
⑵ 若插入结点的某祖先结点的平衡因子的绝对值大于1,则找出其中最小不平衡子树的根结点;
⑶ 判断新插入的结点与最小不平衡子树的根结点的关系,确定是哪种类型的调整;
⑷ 如果是LL型或RR型,只需应用扁担原理旋转一次,在旋转过程中,如果出现冲突,应用旋转优先原则调整冲突;如果是LR型或LR型,则需应用扁担原理旋转两次,第一次最小不平衡子树的根结点先不动,调整插入结点所在子树,第二次再调整最小不平衡子树,在旋转过程中,如果出现冲突,应用旋转优先原则调整冲突;
⑸ 计算调整后的平衡二叉树中各结点的平衡因子,检验是否因为旋转而破坏其他结点的平衡因子,以及调整后的平衡二叉树中是否存在平衡因子大于1的结点。 参考技术A 对于任何一个节点都满足左右子树的深度差不大于1 参考技术B 在树上的每一个节点都满足:它的左右子树的高度差的绝对值不大于1 参考技术C 形态匀称的二叉树称为平衡二叉树 (Balanced binary tree) ,其严格定义是:
一棵空树是平衡二叉树;若 T 是一棵非空二叉树,其左、右子树为 TL 和 TR ,令 hl 和 hr 分别为左、右子树的深度。当且仅当
①TL 、 TR 都是平衡二叉树;
② | hl - hr |≤ 1;
时,则 T 是平衡二叉树。 参考技术D
平衡二叉树(AVL)
那对图 1 进行下改造,把数据重新节点重新连接下,图 2 如下:

图 2 可以看到以下特性:
1. 所有左子树的节点都小于其对应的父节点(4,5,6)<(7);(4)<(5);(8)< (9);
2. 所有右子树上的节点都大于其对应的父节点(8,9,10)>(7);(6)>(5);(10)>(9);
3. 每个节点的平衡因子差值绝对值 <=1;
4. 每个节点都符合以上三个特征。
满足这样条件的树叫平衡二叉树(AVL)树。
问:那再次查找节点 5,需要遍历多少次呢?
由于数据是按照顺序组织的,那查找起来非常快,从上往下找:7-5,只需要在左子树上查找,也就是遍历 2 次就找到了 5。假设要找到叶子节点 10,只需要在右子树上查找,那也最多需要 3 次,7-9-10。也就说 AVL 树在查找方面性能很好,最坏的情况是找到一个节点需要消耗的次数也就是树的层数, 复杂度为 O(logN)
如果节点非常多呢?假设现在有 31 个节点,用 AVL 树表示如图 3:

图 3 是一棵高度为 4 的 AVL 树,有 5 层共 31 个节点,橙色是 ROOT 节点,蓝色是叶子节点。对 AVL 树的查找来看起来已经很完美了,能不能再优化下?比如,能否把这个节点里存放的 KEY 增加?能否减少树的总层数?那减少纵深只能从横向来想办法,这时候可以考虑用多叉树。
算法素颜:玩平衡二叉树就像跷跷板一样简单!
引言
在上一篇中提到了:平衡二叉树的目的就是使得平均查找长度最短。那么这里就引出两个问题:
什么是平衡二叉树?
为什么平衡二叉树的平均查找长度最短?
如何将非平衡二叉树调整成平衡二叉树?
1. 平衡二叉树是什么鬼?
满足如下两个条件的二叉树称为“平衡二叉树”:
首先它得是二分查找树
然后它的左右子树的高度相差不超过1
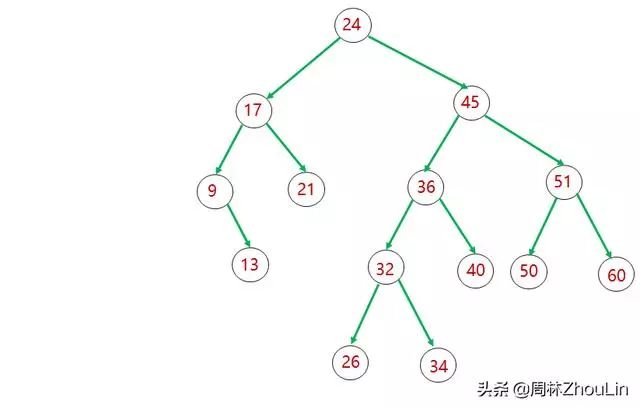
图1 平衡二叉树
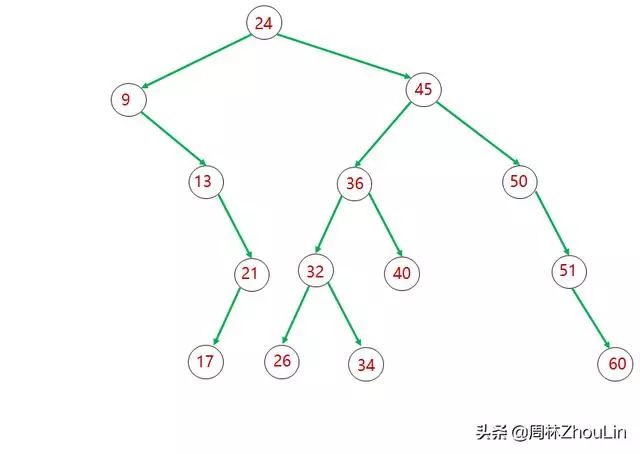
图2 非平衡二叉树
图1就是一棵平衡二叉树,而图2不是平衡二叉树。
在图2中,对于值为9的节点,它的左子树为空,高度为0,右子树高度为3,两者相差3,不满足平衡二叉树定义的第二条规则。
2. 如何证明平衡二叉树的平均查找长度最短?
首先研究一下平衡二叉树与非平衡二叉树的关系。
图3表示的是一棵平衡二叉树,与它对应的任意一棵非平衡二叉树都可以重复按照如下方式变换而来——在维持二分查找树的前提下,从高度较小的子树中取出一个节点A,插入到高度较大的子树中——如图4所示。
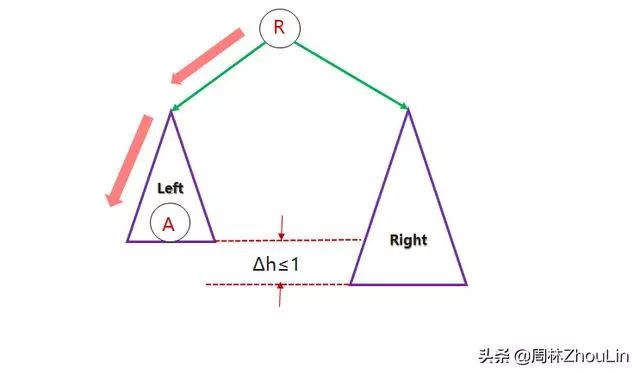
图3 平衡二叉树与非平衡二叉树的转换
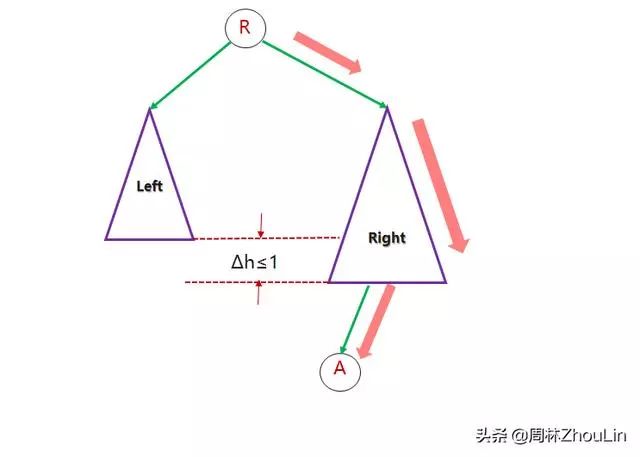
图4 平衡二叉树与非平衡二叉树的转换
接下来用反证法来证明:
假设平衡二叉树的平均查找长度L并不是最短的,那么必然存在一棵非平衡二叉树的平均查找长度L'<L (命题1)
对应到上面的图示就是:
图3的平衡二叉树的平均查找长度L>图4的非平衡二叉树的平均查找长度L'(假设1)
假设1其实是命题1的充分条件,也就是说:只要假设1为真,命题1必为真。
图3的节点总数=图4的节点总数,设为N;
设节点A在图3中的查找长度(从根节点到A所需要的比较次数)为La,在图4中的查找长度为La’,则根据平均查查长度的定义
平均查找长度=每个节点的查找长度之和/节点总数
得到:
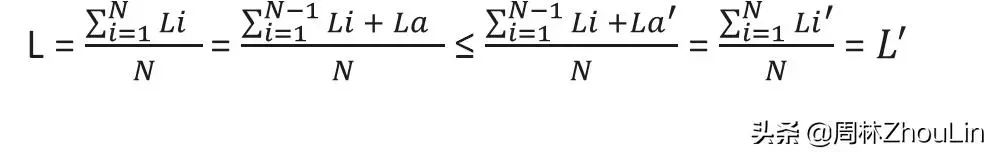
显然上式与前面的假设1矛盾,从而证明了平衡二叉树的平均查找长度最短。
3. 如何将非平衡二叉树调整成平衡二叉树?
朴素的想法就是:遍历每个节点,检查它的左右子树高度,若高度之差超过1,设法交换一些节点的位置,使得该位置左右子树新的高度差缩减到1以内。
这里牵扯出3个问题:
遍历的方向:自顶向下还是自底向上?
遍历的时候如何方便地获取左右子树的高度?
如何交换节点的位置,使得新的高度差在1以内?
对于问题1,如果你仔细研究过笔者前几篇文章的话————那么你很容易得出结论:
两个方向都可以:自顶向上的话,写递归式算法;自底向上的话,写非递归式算法。
这里的“顶”指的是二叉树的根节点,“底”指的是二叉树的尾节点。
对于问题2,取决于问题1采用哪种方式——如果采用递归式算法,那么在递归的时候,也顺便把高度递归计算了;如果采用非递归式,那么就在自底向上归并的时候,动态计算高度。
问题3才是真正的新鲜问题。图5和图6分别描述了一般情况。
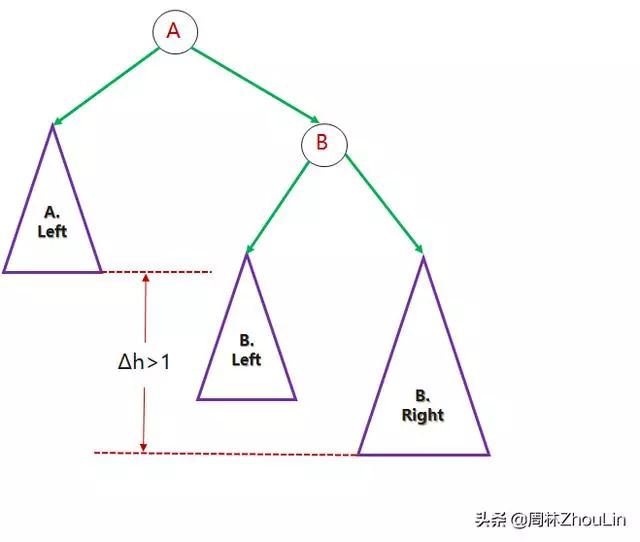
图5
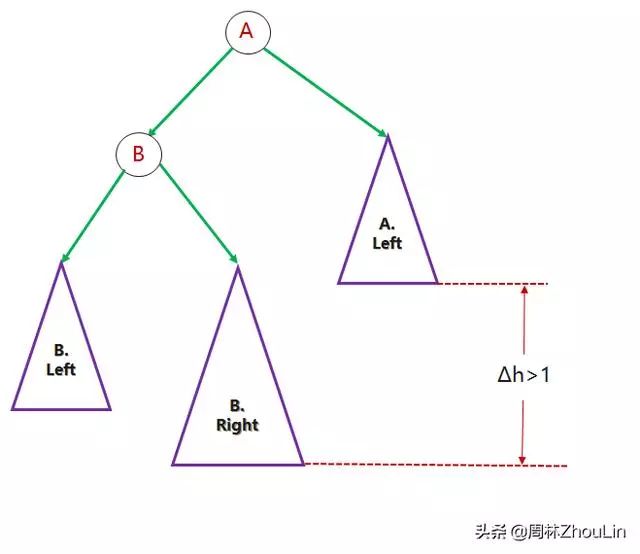
图6
为了解决这个“新鲜问题”,我们先来看一个引理:
引理12.1
因为任意非叶子节点A,它的值都比其右孩子B的值小,所以它可以变成B的左孩子。这样变换之后,A、A的左子树下降,B、B的右子树上升,高度差变小。
因为任意非叶子节点A,它的值都比其左孩子C的值大,所以它可以变成C的右孩子。这样变换之后,A、A的右子树下降,B、B的左子树上升,高度差变小。
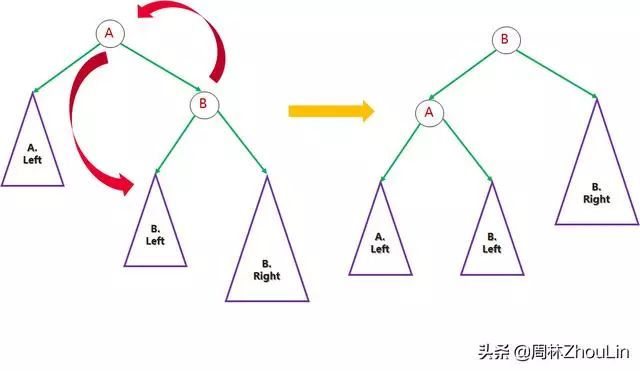
图7
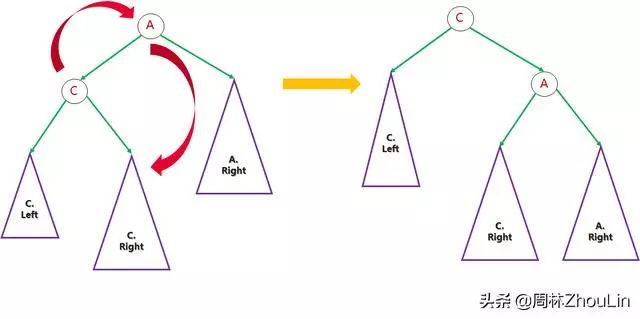
图8
上述的变换是不是很像一种“旋转”:)
那么是不是这样“旋转”之后,调整就OK了呢?答案是否定的。
看看下面这个例子:
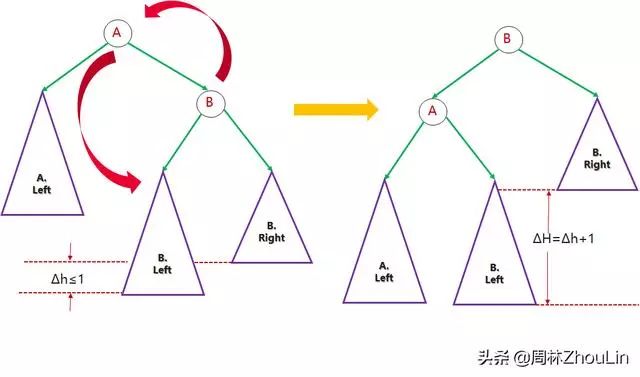
图9
图9中,B节点一开始的左子树高度比其右子树大,即:
H(B.Left)=H(B.Right)+∆h (式1)
“旋转”调整后,B的左子树变成A的右子树,A变成B的左孩子,设高度相对于节点的函数为H,则:
H(A)=Max(H(B.Left), H(A.Left))+1
≥H(B.Left)+1 (式2)
将式1代入式2可得:
H(A)≥H(B.Right)+∆h+1
=H(B.Right)+∆H (式3)
当∆h=1时,∆H=2。
此时H(A)≥H(B.Right)+2,这意味着“旋转”后,B节点的左子树高度与右子树高度相差超过1!
貌似“旋转”对这种情况不凑效了,怎么办呢?
先来分析一下不凑效的根因到底是什么。
从图9可以看出,作为A节点的右孩子,从一开始,B节点的左子树就比其右子树高了一个头,这个是导致后面旋转不凑效的根因。所以很自然地想到:
在旋转前,先把B节点的左子树高度降低或者把右子树高度升高。
那么如何实现上述目标呢?我们能利用的仍然是引理12.1:
先将B节点的左子树展开
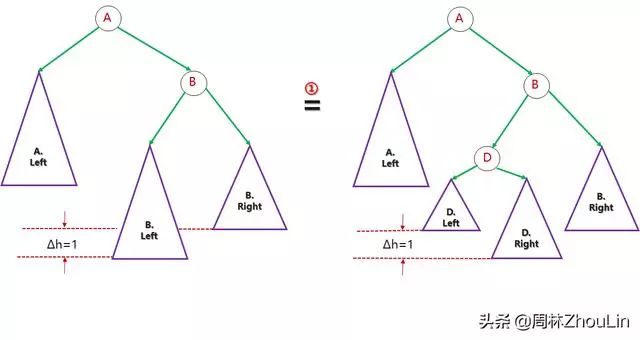
图10
再对展开的子树做一次旋转:
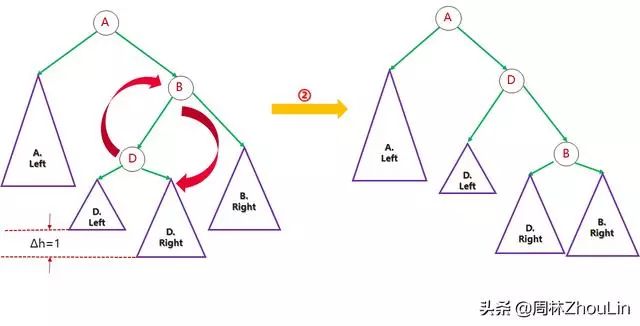
图11
通过以上两步就达成了把原始B节点位置(现在是D节点)的左子树高度降低的目的。
至此就转换成了熟悉的老问题。再做一次旋转便可以彻底调整成平衡二叉树了:
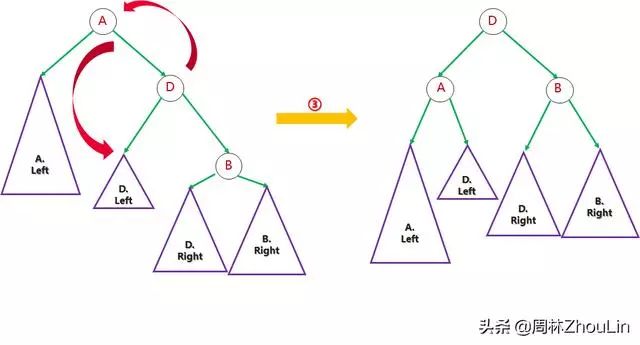
图12
对称地,我们可以用类似的步骤来调整下图的非平衡二叉树:
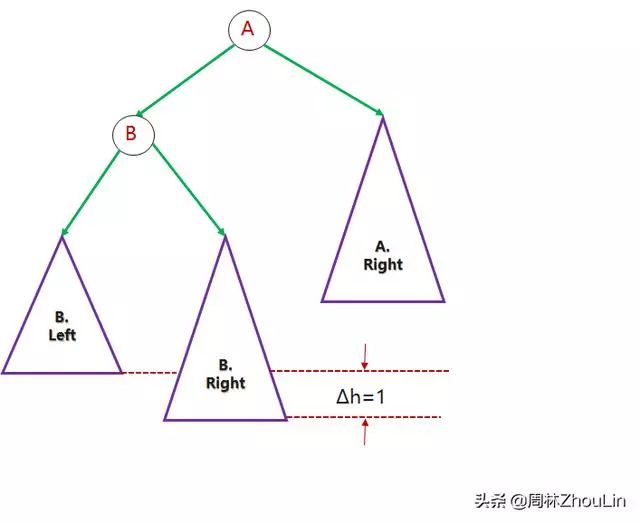
图13
步骤一(子树展开):
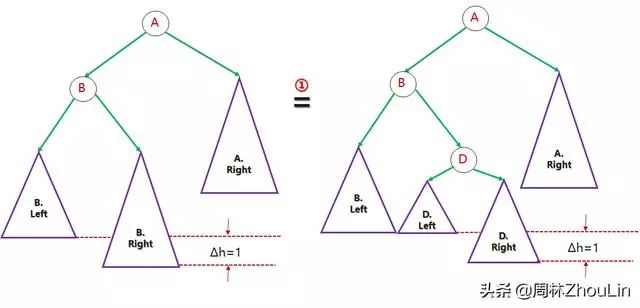
图14
步骤二(一次旋转):
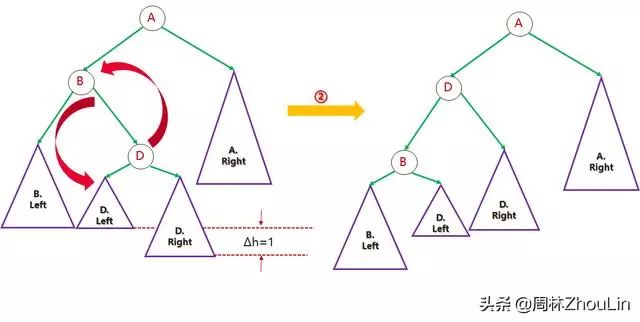
图15
步骤三(二次旋转):
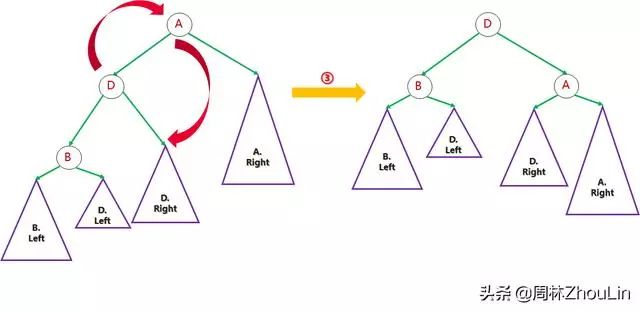
图16
综上所述,自顶向下的、单向链表存储式、递归型平衡二叉树调整算法如下:

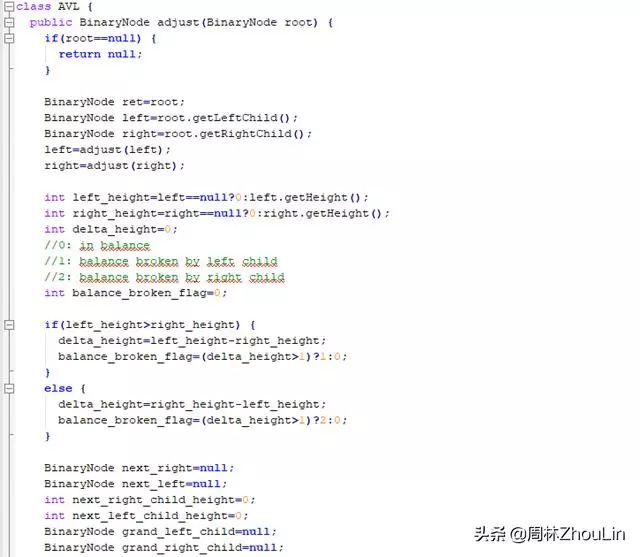
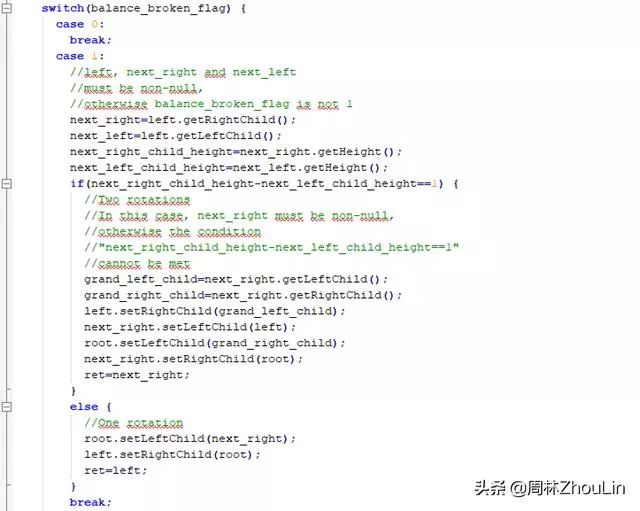
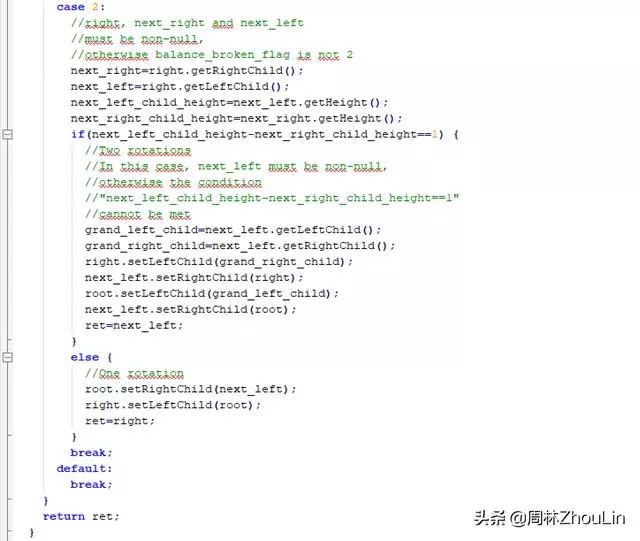
为了节省篇幅,自底向上的、单向链表存储式、非递归型平衡二叉树调整算法和自底向上的、数组存储式、非递归型平衡二叉树调整算法放在下一篇文章里单独列示。
4. 平衡二叉树的节点插入算法
首先平衡二叉树本质是二分查找树,所以插入新节点时,可遵循《无死角“盘”它!二分查找树》中的节点插入算法;
但是平衡二叉树还是特殊的二分查找树,它还要满足左右子树高度相差不超过1的要求。当按照上面的算法插入新节点之后,可能会不满足这个要求,因此要进行调整。调整算法仍然是章节3介绍的旋转调整算法。
5. 平衡二叉树的节点删除算法
首先平衡二叉树本质是二分查找树,所以删除节点时,可遵循《无死角“盘”它!二分查找树》中的节点删除算法;
但是平衡二叉树还是特殊的二分查找树,它还要满足左右子树高度相差不超过1的要求。当按照上面的算法删除节点之后,可能会不满足这个要求,因此要进行调整。调整算法仍然是章节3介绍的旋转调整算法。
是不是很棒!!!分享一下吧,小伙伴们!!!
不存在任何培训机构招生信息!!
以上是关于什么是平衡二叉树的主要内容,如果未能解决你的问题,请参考以下文章