平衡二叉树的作用

Posted 2023-04-19

我们知道，对于一般的二叉搜索树（Binary Search Tree），其期望高度（即为一棵平衡树时）为log2n，其各操作的时间复杂度（O(log2n)）同时也由此而决定。但是，在某些极端的情况下（如在插入的序列是有序的时），二叉搜索树将退化成近似链或链，此时，其操作的时间复杂度将退化成线性的，即O(n)。我们可以通过随机化建立二叉搜索树来尽量的避免这种情况，但是在进行了多次的操作之后，由于在删除时，我们总是选择将待删除节点的后继代替它本身，这样就会造成总是右边的节点数目减少，以至于树向左偏沉。这同时也会造成树的平衡性受到破坏，提高它的操作的时间复杂度。
平衡二叉搜索树（Balanced Binary Tree）具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。常用算法有红黑树、AVL、Treap、伸展树等。在平衡二叉搜索树中，我们可以看到，其高度一般都良好地维持在O（log2n），大大降低了操作的时间复杂度。

参考技术A

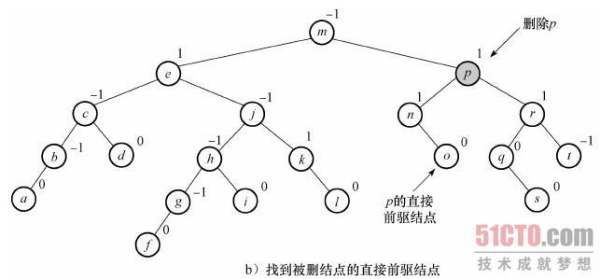
平衡二叉树（AVL）

那对图 1 进行下改造，把数据重新节点重新连接下，图 2 如下：

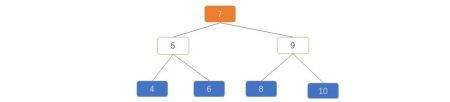
图 2 可以看到以下特性：

1. 所有左子树的节点都小于其对应的父节点（4，5，6）<（7）；（4）<（5）；（8）< （9）；

2. 所有右子树上的节点都大于其对应的父节点（8，9，10）>（7）；（6）>（5）；（10）>（9）；

3. 每个节点的平衡因子差值绝对值 <=1；

4. 每个节点都符合以上三个特征。

满足这样条件的树叫平衡二叉树（AVL）树。

问：那再次查找节点 5，需要遍历多少次呢？

由于数据是按照顺序组织的，那查找起来非常快，从上往下找：7-5，只需要在左子树上查找，也就是遍历 2 次就找到了 5。假设要找到叶子节点 10，只需要在右子树上查找，那也最多需要 3 次，7-9-10。也就说 AVL 树在查找方面性能很好，最坏的情况是找到一个节点需要消耗的次数也就是树的层数， 复杂度为 O(logN)

如果节点非常多呢？假设现在有 31 个节点，用 AVL 树表示如图 3：

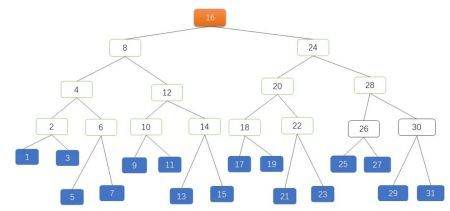
图 3 是一棵高度为 4 的 AVL 树，有 5 层共 31 个节点，橙色是 ROOT 节点，蓝色是叶子节点。对 AVL 树的查找来看起来已经很完美了，能不能再优化下？比如，能否把这个节点里存放的 KEY 增加？能否减少树的总层数？那减少纵深只能从横向来想办法，这时候可以考虑用多叉树。

平衡二叉树的删除

目录

前言

一.结点定义

二.删除

2.1 按照二叉搜索树来删除结点

2.2 更新平衡因子

2.3 检测更新完的平衡因子

三.完整代码

---

前言

        之前再C语言阶段学习了平衡二叉树，用C语言递归实现了一下平衡二叉树的删除与插入。实现如下：数据结构——平衡二叉树(AVL树)之插入和数据结构——平衡二叉树之删除当时学习的时候感觉比较费劲，并且难以理解。

        现在在C++阶段又重新学习了一下平衡二叉树，使用非递归实现，再加上结点引入平衡因子和父节点，感觉更好理解了。

        但是学习的时候，主要时学习了平衡二叉树的插入进一步理解平衡二叉树(插入)。一开始觉得平衡二叉树的删除会和插入如出一辙，只是更新平衡因子会又主要的变化。但是当我实现起来，才发现，它并没有这么简单。

一.结点定义

含有父指针，平衡因子，保存的时键值对pair的结点。

//二叉树应用KV模型
template<class K, class V>
struct AVLTreeNode
{
	AVLTreeNode(const pair<K, V> kv)
	:_left(nullptr)
	, _right(nullptr)
	, _parent(nullptr)
	,_bf(0)
	, _kv(kv)
	{}

	AVLTreeNode *_left;//该节点的左孩子
	AVLTreeNode *_right;//该节点的右孩子
	AVLTreeNode *_parent;//该节点的父亲
	//平衡因子
	int _bf;
	//保存的是键值对，pair结构体
	pair<K, V> _kv;
};

二.删除

        删除的步骤和插入的步骤时一样的只是细节上会有区别

1. 按照二叉搜索树取删除一个结点
2. 更新平衡因子
3. 判断更新完的平衡因子，如果超过平衡界限，旋转处理。

        2.1 按照二叉搜索树来删除结点

        首先需要找到删除结点，按照搜索树的性质。当前结点键值key大于删除结点键值key，往左边找，当前结点键值key小于删除结点键值key，往右边找。

        没找到删除失败，找到结点，按照二叉搜索树删除结点的四种情况删除结点(二叉搜索树C++版实现(建议看这)和应用)。

        注意：1.先不要释放结点的空间。为了后面更新结点平衡因子。

                   2.更新父节点。

//按二叉搜索树删除，但是先不释放空间，为了后面作比较
		Node *cur = _root;
		Node *parent = nullptr;
		while (cur){
			//删除结点小于当前结点键值，往左边找
			if (cur->_kv.first > kv.first){
				parent = cur;
				cur = cur->_left;
			}
			//删除结点大于当前结点键值，往右边找
			else if (cur->_kv.first < kv.first){
				parent = cur;
				cur = cur->_right;
			}
			else{
				//找到，四种情况
				if (cur->_left == nullptr&&cur->_right == nullptr){//左右都空
					//为根节点
					if (parent == nullptr){
						delete cur;
						_root = nullptr;
						return true;
					}
					//直接删除
					if (parent->_left == cur){
						
						parent->_left = nullptr;
						
					}
					else{
						
						parent->_right = nullptr;
					}					
					
				}

				if (cur->_left == nullptr&&cur->_right){//左空，右不空
					//为根节点
					if (parent == nullptr){
						_root = cur->_right;
						delete cur;
						return true;
					}
					//父节点指向右边
					if (parent->_left == cur){
						cur->_right->_parent = parent;
						parent->_left = cur->_right;
					}
					else {
						cur->_right->_parent = parent;
						parent->_right = cur->_right;
					}
				}

				if (cur->_left&&cur->_right == nullptr){//右空，左不空
					//根节点
					if (parent == nullptr){
						_root = cur->_left;
						delete cur;
						return true;
					}
					//
					if (parent->_left == cur){
						cur->_left->_parent = parent;
						parent->_left = cur->_right;
					}
					else {
						cur->_left->_parent = parent;
						parent->_right = cur->_right;
					}
				}
				if (cur->_left&&cur->_right){//右不空，左不空
					Node *prev = cur;
					parent = cur;
					cur = cur->_right;

					while (cur->_left){
						parent = cur;
						cur = cur->_left;
					}
					K k = cur->_kv.first;
					V v = cur->_kv.second;
					prev->_kv.first = k;
					prev->_kv.second = v;

					if (parent->_left == cur){
						if (cur->_right){
							cur->_right->_parent = parent;
						}
						
						parent->_left = cur->_right;
					}
					else{
						if (cur->_right){
							cur->_right->_parent = parent;
						}
						parent->_right = cur->_right;
					}

				}

2.2 更新平衡因子

        删除更新平衡因子和插入平衡因子相反。根据平衡因子的定义为，右子树子树的高度 - 左子树子树的高度。

        当删除的平衡因子在左子树时，当前结点的平衡因子++，左子树高度减1。

        当删除的平衡因子在右子树时，当前结点的平衡因子 --，右子树高度减1。

//更新平衡因子
if (cur->_kv.first < parent->_kv.first){
    parent->_bf++;
}
else{
    parent->_bf--;
}

        为什么先释放掉删除的cur结点？

        更新平衡因子时，根据键值大小来判断在左子树还是右子树。

2.3 检测更新完的平衡因子

        平衡因子的更新时兄下往上更新的，并且只会影响到删除结点的父节点或者祖先结点的平衡因子。但是，不一定影响的全部。

        此时平衡因子只会有三种情况。

• 更新完结点的平衡因子等于0，此时需要继续往上更新。此时，没删除时，结点的平衡因子要不是1，要不是-1，更新完后，平衡因子等于0，说明高度减少，会对上面结点的平衡因子产生影响。

else if (parent->_bf == 0){//高度降低，继续更新
    cur = parent;
    parent = parent->_parent;
}

• 更新完结点的平衡因子等于1或者-1，此时不需要继续往上更新。没删除结点时，结点的平衡因子等于0，这个结点肯定有儿子结点，并且一定左右儿子结点都存在，因为删除的就是这个结点的儿子结点。结点的高度并没有变化，对上面结点不会产生影响。

if (parent->_bf == 1 || parent->_bf == -1){//高度没变
    break;
}

• 更新完结点的平衡因子等于2或者-2，此时超过平衡因子的界限，需要旋转处理。

重点说一下，更新完平衡因子等于2的情况。

        平衡因子等于2或者-2，需要进行旋转处理。旋转是将高度相对另外一边高得一边的高度降下来。

        我们需要通过当前结点高的一边的子节点来判断用什么旋转方式。

        我们删除的是cur结点，更新的是parent结点。如下图。

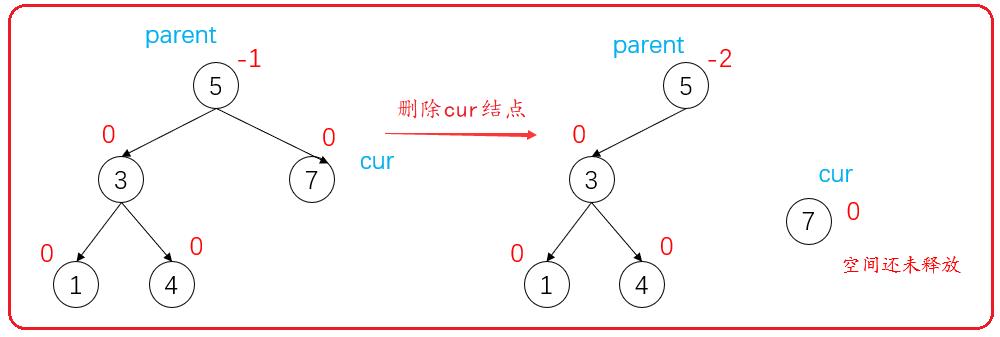
         所以我们需要得到删除结点的另外一边结点，来判断用哪种旋转。此时cur不代表删除结点了。需要用一个结点保存cur结点，方便最后删除。

//最后删除
Node *tail = cur;

//cur所在子树高度降低，另外一边相对时升高了，看升高这边
if (parent->_kv.first > cur->_kv.first){
    cur = parent->_right;
}
else{
    cur = parent->_left;
}

此时使用的旋转，处理插入的四种情况外，还增加了两种情况。

if (parent->_bf == 2 && cur->_bf == 1){//需要继续往上更新
							
	SigelLeft(parent);
	cur = parent->_parent;
	parent = cur->_parent;
}
else if (parent->_bf == 2 && cur->_bf == 0){
    SigelLeft(parent);
    parent->_bf = 1;
    parent->_parent->_bf = -1;
    break;
}
else if (parent->_bf == 2 && cur->_bf == -1){//需要继续往上更新
							
    DoubleRightLeft(parent);
    cur = parent->_parent;
    parent = cur->_parent;
							
}

else if (parent->_bf == -2 && cur->_bf == -1){//需要继续往上更新
							
    SigelRight(parent);
    cur = parent->_parent;
    parent = cur->_parent;
}
else if (parent->_bf == -2 && cur->_bf == 0){
    SigelRight(parent);
    parent->_bf = -1;
    parent->_bf = 1;
    break;
}
else if (parent->_bf == -2 && cur->_bf == 1){//需要继续往上更新
							
    DoubleLeftRight(parent);
    cur = parent->_parent;
    parent = cur->_parent;
}

        首先说明，插入的四种情况还需要继续往上更新。了解旋转就知道，插入的四种情况旋转完后，根节点的平衡因子从不平衡都变成了0，没更新前平衡因子肯定是-1或者1(不然怎么更新到2的)，此时高度降低了。需要继续往上更新。

想了解这四种情况的可以看博客：进一步理解平衡二叉树

        还多出两种情况：

• parent->_bf == 2 && cur->_bf == 0，父结点为2，当前结点为0。

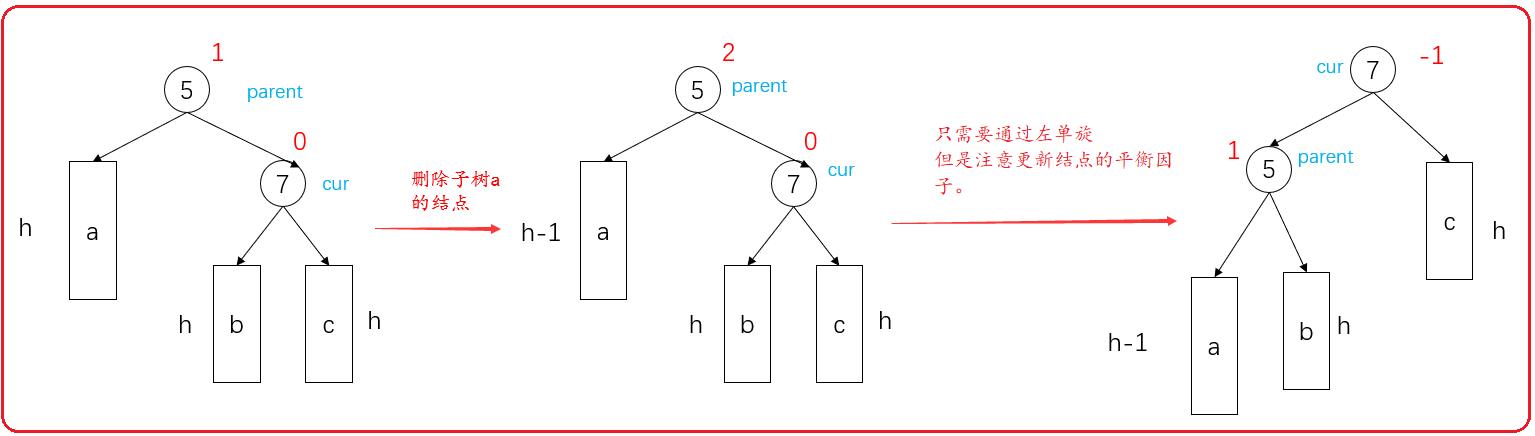
        此时只需要进行左单旋即可，但是，注意要重新更新parent和cur的平衡因子。

        由于结点没更新前的平衡因子就是1或者-1，旋转后，结点的平衡因子还是1或者-1，高度没变。不需要继续往上更新。

• parent->_bf == -2 && cur->_bf == 0，父节点(更新的)平衡因子等于-2，当前结点的平衡因子等于0。

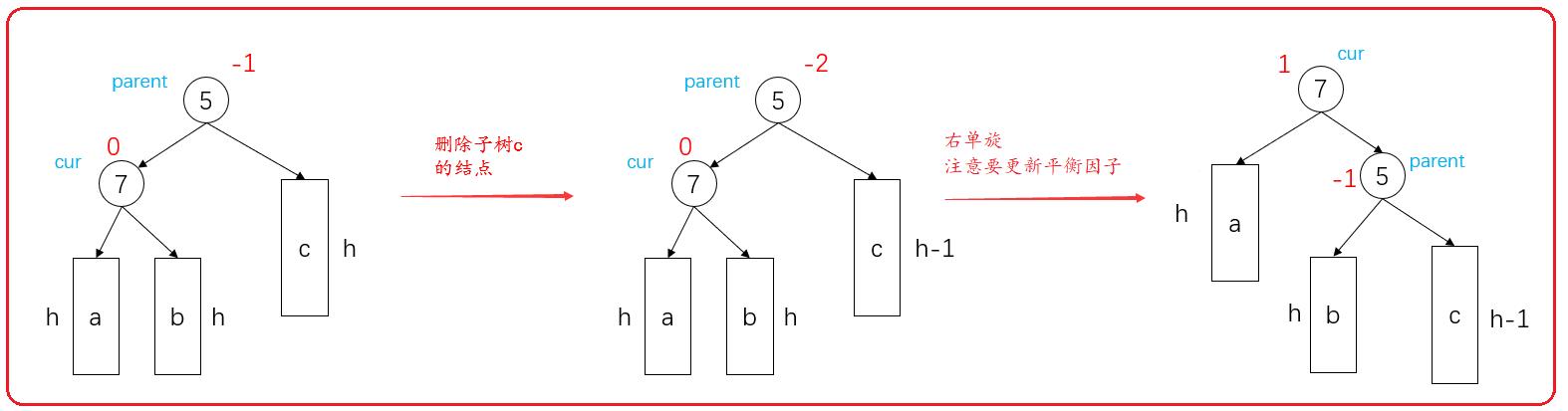
         此时只需要进行右单旋即可，但是，注意要重新更新parent和cur的平衡因子。

        由于结点没更新前的平衡因子就是1或者-1，旋转后，结点的平衡因子还是1或者-1，高度没变。不需要继续往上更新。

三.完整代码

#pragma once
#include<iostream>
using namespace std;

//二叉树应用KV模型
template<class K, class V>
struct AVLTreeNode
{
	AVLTreeNode(const pair<K, V> kv)
	:_left(nullptr)
	, _right(nullptr)
	, _parent(nullptr)
	,_bf(0)
	, _kv(kv)
	{}

	AVLTreeNode *_left;//该节点的左孩子
	AVLTreeNode *_right;//该节点的右孩子
	AVLTreeNode *_parent;//该节点的父亲
	//平衡因子
	int _bf;
	//保存的是键值对，pair结构体
	pair<K, V> _kv;
};

template<class K,class V>
class AVLTree
{
	typedef AVLTreeNode<K,V> Node;
public:
	bool insert(const pair<K, V> kv)
	{
		if (_root == nullptr){
			_root = new Node(kv);
			return true;
		}
		Node *cur = _root;
		Node *parent = nullptr;
		while (cur)
		{
			if (kv.first > cur->_kv.first){
				parent = cur;
				cur = cur->_right;
			}
			else if (kv.first < cur->_kv.first){
				parent = cur;
				cur = cur->_left;
			}
			else{
				return false;
			}
		}
		//找到插入位置，现在进行插入
		cur = new Node(kv);
		//要更新父节点
		cur->_parent = parent;
		if (parent->_kv.first < kv.first){
			
			parent->_right = cur;
		}
		else{
			
			parent->_left = cur;
		}

		//更新平衡因子
		while (parent){
			//如果插入左边平衡因子--
			if (parent->_left == cur){
				parent->_bf--;
			}
			//如果插入右边，平衡因子++
			else{
				parent->_bf++;
			}

			//判断平衡因子
			if (parent->_bf == 0){//如果parent位置平衡因子等于0，不再往上更新，高度没变
				break;
			}
			else if (parent->_bf == 1 || parent->_bf == -1){//高度变了，但是没有不平衡，继续往上更新
				cur = parent;
				parent = parent->_parent;
			}
			else if (parent->_bf == 2 || parent->_bf == -2){//不平衡需要旋转
				if (parent->_bf == 2 && cur->_bf == 1){
					SigelLeft(parent);//左单旋
				}
				else if (parent->_bf == 2 && cur->_bf == -1){
					DoubleRightLeft(parent);//右左双旋
				}
				else if (parent->_bf == -2 && cur->_bf == 1){
					DoubleLeftRight(parent);//左右双旋
				}
				else if (parent->_bf == -2 && cur->_bf == -1){
					SigelRight(parent);//右单旋
				}
				break;//旋转完不需要更新平衡因子了。

			}
			else{
				
			}
		}
		return true;


	}
	bool erase(pair<K,V> kv){
		//按二叉搜索树删除，但是先不释放空间，为了后面作比较
		Node *cur = _root;
		Node *parent = nullptr;
		while (cur){
			//删除结点小于当前结点键值，往左边找
			if (cur->_kv.first > kv.first){
				parent = cur;
				cur = cur->_left;
			}
			//删除结点大于当前结点键值，往右边找
			else if (cur->_kv.first < kv.first){
				parent = cur;
				cur = cur->_right;
			}
			else{
				//找到，四种情况
				if (cur->_left == nullptr&&cur->_right == nullptr){//左右都空
					//为根节点
					if (parent == nullptr){
						delete cur;
						_root = nullptr;
						return true;
					}
					//直接删除
					if (parent->_left == cur){
						
						parent->_left = nullptr;
						
					}
					else{
						
						parent->_right = nullptr;
					}					
					
				}

				if (cur->_left == nullptr&&cur->_right){//左空，右不空
					//为根节点
					if (parent == nullptr){
						_root = cur->_right;
						delete cur;
						return true;
					}
					//父节点指向右边
					if (parent->_left == cur){
						cur->_right->_parent = parent;
						parent->_left = cur->_right;
					}
					else {
						cur->_right->_parent = parent;
						parent->_right = cur->_right;
					}
				}

				if (cur->_left&&cur->_right == nullptr){//右空，左不空
					//根节点
					if (parent == nullptr){
						_root = cur->_left;
						delete cur;
						return true;
					}
					//
					if (parent->_left == cur){
						cur->_left->_parent = parent;
						parent->_left = cur->_right;
					}
					else {
						cur->_left->_parent = parent;
						parent->_right = cur->_right;
					}
				}
				if (cur->_left&&cur->_right){、
					Node *prev = cur;
					parent = cur;
					cur = cur->_right;

					while (cur->_left){
						parent = cur;
						cur = cur->_left;
					}
					K k = cur->_kv.first;
					V v = cur->_kv.second;
					prev->_kv.first = k;
					prev->_kv.second = v;

					if (parent->_left == cur){
						if (cur->_right){
							cur->_right->_parent = parent;
						}
						
						parent->_left = cur->_right;
					}
					else{
						if (cur->_right){
							cur->_right->_parent = parent;
						}
						parent->_right = cur->_right;
					}

				}
				//最后删除
				Node *tail = cur;
				
				while (parent){
					//更新平衡因子
					if (cur->_kv.first < parent->_kv.first){
						parent->_bf++;
					}
					else{
						parent->_bf--;
					}

					//检测平衡因子
					if (parent->_bf == 1 || parent->_bf == -1){//高度没变
						break;
					}
					else if (parent->_bf == 0){//高度降低，据徐更新
						cur = parent;
						parent = parent->_parent;
					}
					else if (parent->_bf == 2 || parent->_bf == -2){
						//cur所在子树高度降低，另外一边相对时升高了，看升高这边
						if (parent->_kv.first > cur->_kv.first){
							cur = parent->_right;
						}
						else{
							cur = parent->_left;
						}

						if (parent->_bf == 2 && cur->_bf == 1){//需要继续往上更新
							
							SigelLeft(parent);
							cur = parent->_parent;
							parent = cur->_parent;
						}
						else if (parent->_bf == 2 && cur->_bf == 0){
							SigelLeft(parent);
							parent->_bf = 1;
							parent->_parent->_bf = -1;
							break;
						}
						else if (parent->_bf == 2 && cur->_bf == -1){//需要继续往上更新
							
							DoubleRightLeft(parent);
							cur = parent->_parent;
							parent = cur->_parent;
							
						}

						else if (parent->_bf == -2 && cur->_bf == -1){//需要继续往上更新
							
							SigelRight(parent);
							cur = parent->_parent;
							parent = cur->_parent;
						}
						else if (parent->_bf == -2 && cur->_bf == 0){
							SigelRight(parent);
							parent->_bf = -1;
							parent->_bf = 1;
							break;
						}
						else if (parent->_bf == -2 && cur->_bf == 1){//需要继续往上更新
							
							DoubleLeftRight(parent);
							cur = parent->_parent;
							parent = cur->_parent;
						}
						

					}

				}
				delete tail;
				return true;

			}
		}
		//没找到
		return false;


	}

	void SigelLeft(Node *parent){
		Node *SubR = parent->_right;
		Node *SubRL = SubR->_left;

		Node *Pparent = parent->_parent;
		//注意要更新父节点
		parent->_right = SubRL;
		if (SubRL){
			SubRL->_parent = parent;
		}

		SubR->_left = parent;
		parent->_parent = SubR;

		//更新新根节点SubR的父节点
		if (Pparent == nullptr){//当前结点为根节点
			//直接置空
			SubR->_parent = nullptr;
			//注意要更新根节点
			_root = SubR;
		}
		else{//当前树为子树
			//连接到上面结点
			if (Pparent->_kv.first < SubR->_kv.first){
				Pparent->_right = SubR;
				
			}
			else{
				Pparent->_left = SubR;
			}

			//更新父节点
			SubR->_parent = Pparent;
		}

		SubR->_bf = 0;
		parent->_bf = 0;
	}

	void SigelRight(Node *parent){
		Node *SubL = parent->_left;
		Node *SubLR = SubL->_right;

		Node *Pparent = parent->_parent;

		parent->_left = SubLR;
		if (SubLR){
			SubLR->_parent = parent;
		}

		SubL->_right = parent;
		parent->_parent = SubL;

		if (Pparent == nullptr)//根节点
		{
			
			SubL->_parent = nullptr;
			_root = SubL;
		}
		else//子树
		{
			if (Pparent->_kv.first > SubL->_kv.first){
				Pparent->_left = SubL;
			}
			else{
				Pparent->_right = SubL;
			}
			SubL->_parent = Pparent;
		}

		SubL->_bf = 0;
		parent->_bf = 0;
	}

	void DoubleRightLeft(Node *parent){
		Node *SubR = parent->_right;
		Node *SubRL = SubR->_left;

		//为了后面更新平衡因子，看插入左边还是右边
		int bf = SubRL->_bf;

		SigelRight(SubR);

		SigelLeft(parent);
		//画图理解,更新平衡因子
		if (bf == 1){//插入方向在右边
			SubR->_bf = 0;
			SubRL->_bf = 0;
			parent->_bf = -1;
		}
		else if (bf == -1){//插入方向在左边
			SubRL ->_bf= 0;
			parent->_bf = 0;
			SubR->_bf = 1;
		}
		else if (bf == 0){//SubRL就是插入结点
			SubR->_bf = 0;
			SubRL->_bf = 0;
			parent->_bf = 0;
		}
	}

	void DoubleLeftRight(Node *parent){
		Node *SubL = parent->_left;
		Node *SubLR = SubL->_right;

		int bf = SubLR->_bf;

		SigelLeft(SubL);

		SigelRight(parent);

		if (bf == 1){
			SubL->_bf = -1;
			parent->_bf = 0;
			SubLR->_bf = 0;
		}
		else if (bf == -1){
			parent->_bf = 1;
			SubL->_bf = 0;
			SubLR->_bf = 0;
		}
		else if (bf == 0){
			parent->_bf = 0;
			SubL->_bf = 0;
			SubLR->_bf = 0;
		}
	}


	int _Height(Node *root){
		if (root == nullptr){
			return 0;
		}
		int left = _Height(root->_left);
		int right = _Height(root->_right);

		return left > right ? left + 1 : right + 1;
	}

	bool _IsBalanceTree(Node *pRoot)
	{


		// 空树也是AVL树
		if (nullptr == pRoot) return true;
		// 计算pRoot节点的平衡因子：即pRoot左右子树的高度差
		int leftHeight = _Height(pRoot->_left);
		int rightHeight = _Height(pRoot->_right);
		int diff = rightHeight - leftHeight;
		// 如果计算出的平衡因子与pRoot的平衡因子不相等，或者
		// pRoot平衡因子的绝对值超过1，则一定不是AVL树
		if (diff != pRoot->_bf || (diff > 1 || diff < -1))
			return false;
		// pRoot的左和右如果都是AVL树，则该树一定是AVL树
		return _IsBalanceTree(pRoot->_left) && _IsBalanceTree(pRoot->_right);
	}

	bool Isbalance(){
		return _IsBalanceTree(_root);
	}
    //中序遍历
	void _InOrder(Node *root){
		if (root){
			_InOrder(root->_left);
			cout << root->_kv.first;
			_InOrder(root->_right);
		}
	}

	void InOrder(){
		_InOrder(_root);
		cout << endl;
	}

private:
	Node *_root = nullptr;
};