最小二乘法 (转)good
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了最小二乘法 (转)good相关的知识,希望对你有一定的参考价值。
最小二乘法也称为最小平方法,是一种数据优化技术,它通过最小化误差的平方和寻找数据的最佳函数匹配。
最小二乘法最初由高尔顿在创立回归分析的时候提出,现在已经成为探索变量间关系最重要的方法,最小二乘法根据其数学原理命名,即误差平方和最小,在误差平方和最小状态下进行函数参数估计,可认为是参数的最佳估计。
一、问题的提出
我们在研究变量间的关系时,会收集一定量的数据样本,这些数据在二维坐标图上呈现为一个个的数据点,理论上来讲,如果变量间存在确定的已知函数关系,则函数图像(曲线或直线)会经过所有的数据点,而通常我们得到的数据都是样本数据,样本数据存在误差,导致我们根据样本数据计算出的函数和已知函数也存在误差,其函数图像无法经过所有数据点。
误差使得多次试验的样本数据所呈现的函数图像会不同,即使是同一组样本数据,如果没有统一的标准,那么不同的人去描绘所呈现的函数图像也会不同。
而我们就是要找到一条标准,使得从这些存在误差的样本数据中求出一个近似函数,使得它和已知函数最为接近,这个近似函数的图像不一定要经过所有的数据点,但是要尽可能的使所有数据点对称且均匀的分布在其两侧,并且这条线既能反映数据的总体分布,也不至于出现局部的较大波动,通过一个近似函数去拟合已知函数,这样就是曲线拟合问题。
一般来说。曲线拟合的任务有两个:
1.当变量间的函数关系已知,只是其中的常数未知,根据数据点拟合出各常数的最佳估计值。
2.当变量间的函数关系未知,根据数据点拟合出变量间函数关系的经验公式,并求出其中各常数的最佳估计值。
二、问题的解决
前面说过,如果没有一条标准,可以找到无数个近似函数,我们可以按照以下原则进行思考:
1.为了精确而全面的描述变量间的关系,必须使用这组变量的全部观察值(实际上很难做到,一般都使用样本数据)
2.确定变量间的关系是直线还是曲线,要根据协方差或相关系数进行判断
3."最好"的近似函数,应该和已知函数偏差最小,对于函数图像来说,就是所有数据点到这个函数图像(曲线或直线)的垂直距离的和最小。
按照以上原则,我们来进行分析:
设已知函数y=f(x),近似函数为φ(x)
令δi=yi-φ(xi)
δi就是残差,让残差最小,有不同的方法

其中第四种——偏差的平方和最小,就是最小二乘法。
在实际应用中,样本数据并不都是等精度、等地位的,对于精度高、地位重的数据应该给予更大的权重,这时要使用加权最小二乘法。
===============================================================
使用最小二乘法估计出的回归方程具有以下性质:
1.无偏性
可以证明最小二乘法估计出的回归方程中各参数的期望(均值)等于真实方程中的参数值
假设一个线性回归方程的形式如下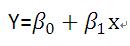
使用最小二乘估计出的回归方程为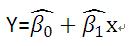
则有
2.线性
可以证明使用最小二乘法估计出的参数是Y的线性函数
3.最小方差性
对同一个样本,使用不同的方法进行估计,会得到不同的参数,这些参数也可能是无偏的和线性的,但是在这些参数中,可以证明使用最小二乘法估计出的参数方差最小。
以上三个性质也是评价一个参数是否为优良参数的参考标准,由于最小二乘法估计量同时具备这三条性质,因此也称为最小二乘法估计量为最佳线性无偏估计量best linear unbiased estimate,简称BLUE
在高斯经典假设条件下,我们不需要再去寻找其它无偏估计量,没有一个会优于普通最小二乘估计量。也就是说,如果存在一个好的线性无偏估计量,这个估计量的方差最多与普通最小二乘估计量的方差一样小,不会小于普通最小二乘估计量的方差,这个定理称为高斯-马尔科夫定理。正是因为最小二乘法估计量具有BLUE性质,才使得最小二乘法得到广泛应用,但是要注意的是,最小二乘估计量这些优良的性质,依赖于高斯基本假设。
对于一个实际的曲线拟合问题,通常的做法是将观测值在二维坐标平面上画出散点图,观察散点图的分布和哪类曲线图接近,然后选用相应的曲线拟合方程,对于有些非线性拟合曲线可以通过适当的变量替换转化为线性拟合曲线,按照线性拟合进行处理,这样会简便一些,下图列举了一些常见的变换
http://www.cnblogs.com/xmdata-analysis/p/5048446.html
以上是关于最小二乘法 (转)good的主要内容,如果未能解决你的问题,请参考以下文章