线性模型的最小二乘法拟合(转)
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了线性模型的最小二乘法拟合(转)相关的知识,希望对你有一定的参考价值。
我们知道在二维坐标中,已知两点就可以确定一个线性方程,如果有n个数据点(x1,y1),(x2,y2),...(xn,yn),那么就会有n个线性方程,我们使用最小二乘法从这n个方程中拟合出一个最佳的线性方程,也就是求出方程的参数a,b
设某个已知的一元线性方程的表达式为:
y=a+bx
有一组权重相等的测量数据(xi,yi),假定自变量xi的误差可以忽略,那么在某个自变量xi下,对应的测量数据为yi,线性方程上的点为a+bxi,二者的偏差为
di=yi-(a+bxi),如果测量数据yi恰好都落在线性方程上,那么d1=d2=...=di=0,此时求出的a,b无疑使最佳的,但由于误差存在,这是不可能出现的情况,因此只要
考虑所有的偏差d1+d2+...di最小,由于d有正有负,相加会互相抵消,而取绝对值又不好解方程,因此采用平方和的形式,即d12+d22+...di2,在d12+d22+...di2为最小值的情况下,求出的a,b为最佳拟合。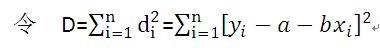
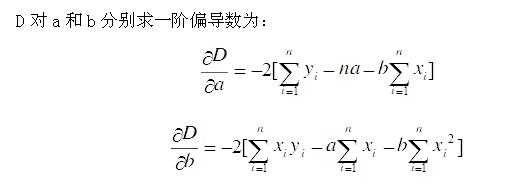


以上是关于线性模型的最小二乘法拟合(转)的主要内容,如果未能解决你的问题,请参考以下文章
最小二乘法拟合非线性函数及其Matlab/Excel 实现(转)